Equação de Bernoulli: aprenda de uma vez!

Você provavelmente, durante sua graduação, já deve ter ouvido falar sobre a equação de Bernoulli ou a fórmula de Bernoulli e suas diversas aplicações nos mais variados ramos da engenharia.

Mas afinal, você conhece bem a equação de Bernoulli?

Sabe quando podemos aplicar na prática a equação e quais suas principais limitações?

Te prometo que ao final desse post você saberá os conceitos que envolvem a equação de Bernoulli, além disso saberá a fórmula para fluidos ideais e para fluidos reais e quando utilizar cada uma dessas equações!

Vamos lá?

Conceitos iniciais

Antes de tratarmos diretamente sobre Bernoulli e suas aplicações, traremos alguns conceitos iniciais para facilitar seu entendimento a respeito do conteúdo.

Então, de acordo com um conceito pré-estabelecido pela equação de continuidade, para que a hipótese um regime permanente seja verdadeira, a massa de fluido que flui por uma seção de um tubo de corrente deve ser idêntica àquela que o abandona por outra seção qualquer.

Mas afinal, o que isso quer dizer?

Simplesmente que em um regime permanente, a massa de um fluido não se altera durante o fluxo.

Então você se pergunta, o que é regime permanente e como isso pode ser relacionado com a equação de Bernoulli?

Inicialmente, regime permanente é aquele em que as propriedades do fluido são invariáveis em cada ponto no decorrer do tempo.

Ou seja, ao analisarmos um único ponto do fluido, ele terá as mesmas propriedades durante todo o fluxo.

E respondendo à segunda pergunta, com base no fato de que a energia não pode ser criada nem destruída, é possível construir uma equação que permitirá fazer o balanço das energias, da mesma forma como foi feito para as massas, por meio da equação da continuidade.

A equação de Bernoulli é essa equação!

 

 

Equação de Bernoulli

De maneira bem simplificada, como podemos conceituar a equação de Bernoulli?

A equação de Bernoulli, ou fórmula de Bernoulli, é uma equação que faz um balanço de igualdade entre os diversos tipos de energias de um fluido em seu fluxo.

Ou seja, a equação de Bernoulli é ligada diretamente com a energia de um fluido em seu fluxo!

De maneira geral, podemos enumerar três tipos de energia em um fluido, são elas:

• Energia potencial;
• E. cinética;
• Energia de pressão;

Então, vamos agora falar um pouco mais a respeito de cada uma dessas energias.

Energia Potencial

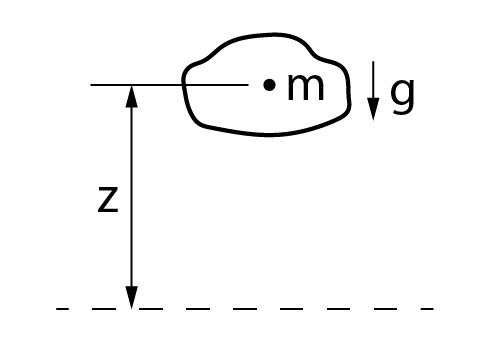
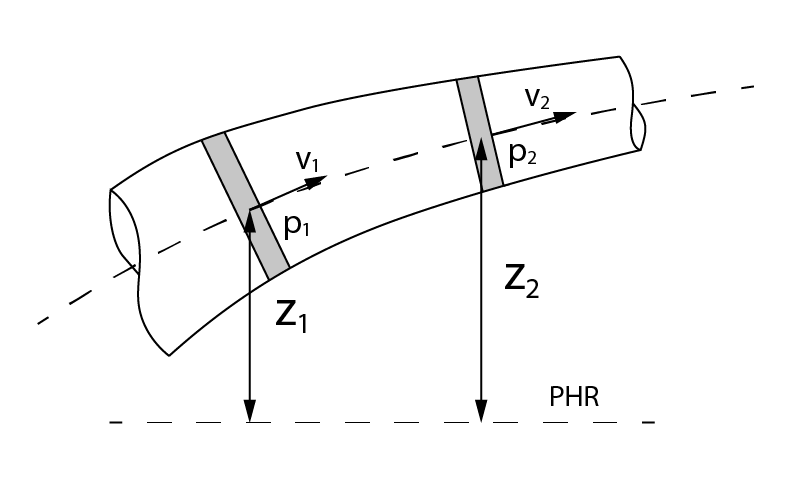
A energia potencial se dá devido à posição no campo da gravidade em relação a um plano horizontal de referência (PHR).

Essa energia é medida pelo potencial de realização de trabalho do sistema.

Energia cinética

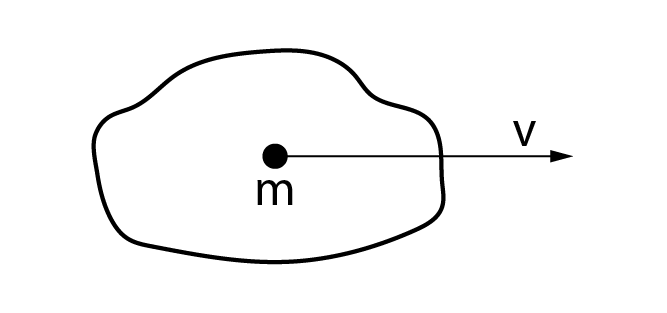
A energia cinética é relacionada com a movimentação do fluido, ou seja, com sua velocidade.

Energia de pressão

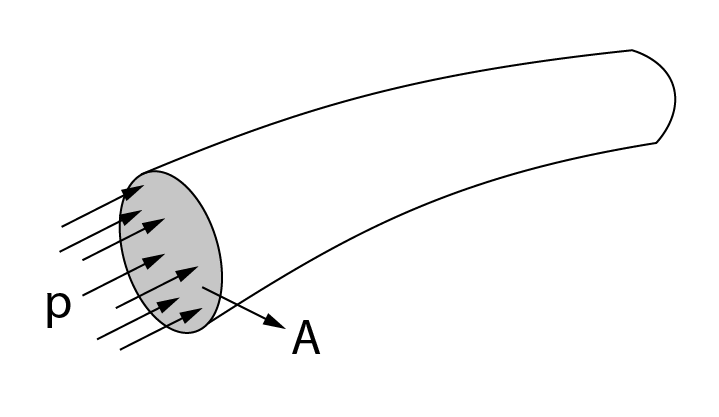
A energia de pressão corresponde ao trabalho potencial das forças de pressão que atuam no escoamento do fluido.

Energia mecânica total

Por fim, podemos dizer que a energia mecânica total é a soma de todas as energias citadas anteriormente.

Então, agora que já sabemos os conceitos das energias em um fluido, iremos tratar diretamente da equação de Bernoulli.

Equação de Bernoulli para fluidos ideais

É importante que você saiba que a equação de Bernoulli é um desenvolvimento da equação de Euller.

Para simplificação, algumas considerações são feitas durante tal desenvolvimento, são elas:

• Regime permanente;
• Sem perdas de carga no escoamento, ou seja, o fluido é considerado um fluido ideal;
• Propriedades uniformes nas seções;
• Fluido incompressível;
• Sem trocas de calor.

Então,

Mas afinal, qual a fórmula da equação de Bernoulli?

A fórmula de Bernoulli é apresentada a seguir:

\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{\gamma } = {z_2} + \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{\gamma }}

Onde:

• z₁ e z₂: distância vertical entre os pontos analisados do fluxo e o plano horizontal de referência;
• v₁ e v₂: velocidade do fluxo nos pontos analisados;
• g: aceleração da gravidade;
• p₁ e p₂: pressão do fluido nos pontos analisados;
• \mathrm{\gamma}: peso específico do fluido analisado.

É possível perceber que, como comentado anteriormente, a equação de Bernoulli é relacionada ao balanço de energia no fluxo de um fluido.

Podemos ainda separar a fórmula em três parcelas, de acordo com os tipos de energia já citados:

• \mathrm{{z_x}}: carga potencial (m);
• \mathrm{\dfrac{{v_x^2}}{{2 \cdot g}}}: carga cinética (m);
• \mathrm{\dfrac{{{p_x}}}{\gamma }}: carga de pressão (m).

Você já sabe os conceitos de cargas potencial, cinética e de pressão.

Então,  vamos agora falar um pouco sobre linha piezométrica e linha de energia.

Linha Piezométrica e linha de de energia

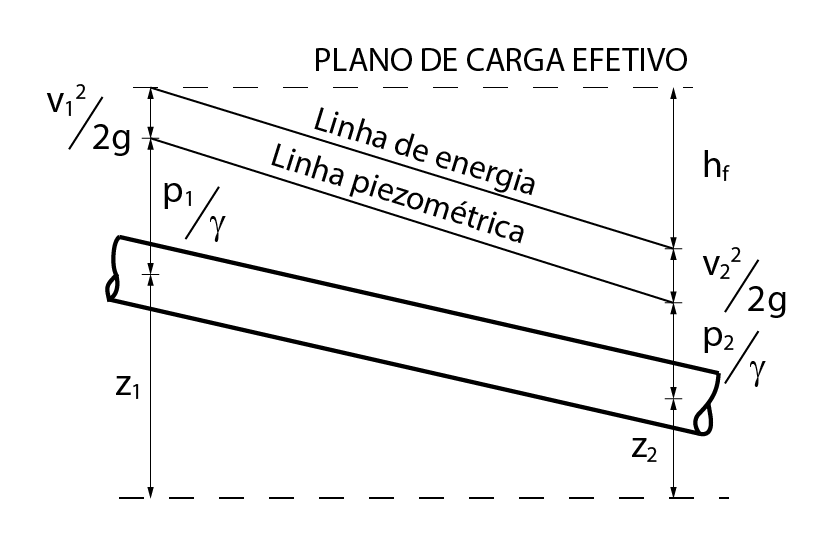
Linha piezométrica é o lugar geométrico dos pontos cujas cotas são dadas pela soma das cargas potencial e de pressão, ou seja:

\mathrm{{z_x} + \dfrac{{{p_x}}}{\gamma }}

Cada valor dessa soma pode ser chamado de cota piezométrica.

Resumindo: cota piezométrica nada mais é do que a soma das cargas potencial e de pressão!

Já a linha de energia em um fluxo é a linha que representa as cotas de energia total em um fluido, ou seja, é a soma da cota piezométrica com a carga cinética.

Se analisarmos matematicamente a equação de Bernoulli para um fluido ideal, vamos perceber que a linha de energia é constante durante todo o fluxo, visto que há uma igualdade entre as energias ao longo do fluxo.

Podemos dizer então que, para um fluido ideal, ou seja, quando não há perda de carga em um fluxo, a energia total é mantida. Porém, isso não é válido para um fluido real.

Mas afinal, o que é perda de carga e o que é um fluido real?

Equação de Bernoulli para fluidos reais

Já vimos que em fluidos ideais não há variação ou perda na energia total do fluxo.

Entretanto, em condições reais, a viscosidade do fluido dá origem a tensões de cisalhamento, por consequência, o fluxo se realiza com uma perda de carga.

Mas Filipe, o que essa perda de carga?

É bem simples: de maneira resumida, a perda de carga é apenas a transformação de energia mecânica em calor e trabalho.

A perda de carga está diretamente relacionada com a turbulência que ocorre no conduto.

Logo, é possível imaginar que, em uma tubulação retilínea, a perda de carga seja menor se comparada com uma tubulação semelhante, mas com uma série de peças especiais, tais como curvas, cotovelos, etc. As peças especiais provocam perdas localizadas pela maior turbulência na região da peça.

Não iremos nos ater aqui ao cálculo das perdas de carga, mas é importante que você saiba que ela ocorre para fluidos reais!

Então, a principal diferença de um fluxo ideal para um fluxo real é que no fluxo real ocorrerá perda de carga, ou seja, a linha de energia não é constante ao longo do fluxo!

Fluido ideal	Fluido real
Incompressível, ou seja, massa específica constante	Pode ser compressível
O fluxo é laminar	O fluxo é turbulento
Não possui viscosidade	Possui viscosidade
Não possui tensão superficial	Possui tensão superficial
Não existem na prática	Ex: água, querosene, petróleo, etc.

Fórmula da equação de Bernoulli para fluidos reais

Podemos concluir, então, que para um fluido real, com perda de carga, a equação de Bernoulli é semelhante a de um fluido ideal, porém, considerando as perdas de carga ao longo do fluxo. Logo, temos:

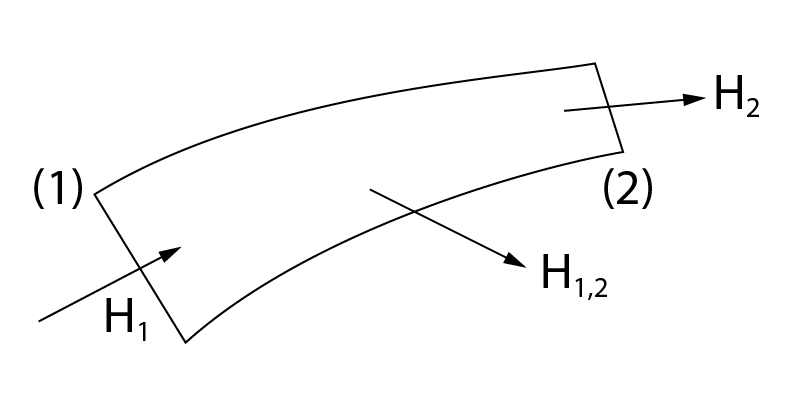
\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{\gamma } = {z_2} + \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{\gamma } + \Delta {H_{12}}}

Onde:

• \mathrm{\Delta {H_{12}}}: perda de carga entre os pontos 1 e 2;

Então, se nós traçarmos as linhas piezométrica e de energia para um fluxo de um fluido real, teríamos uma linha com inclinação negativa ao longo do fluxo, que representa justamente a perda da carga no conduto.

 

Então, por hoje é isso!

Espero que você tenha gostado do conteúdo e que tenha aprendido tudo!

Caso você tenha mais interesse pelo assunto, você pode acessar nosso post sobre aplicações práticas da equação de Bernoulli, onde você verá como essa equação é muito mais utilizada do que você imagina.

Além disso, também temos um  post com a seleção de alguns exercícios resolvidos sobre a equação de Bernoulli!

Espero que eu tenha te ajudado a sanar suas dúvidas sobre o conteúdo!

Caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!