Equação de Bernoulli: exercícios resolvidos

Se você chegou até esse post, parabéns!

Tenho certeza que você já domina o conteúdo de Equação de Bernoulli e também suas aplicações que você aprendeu no nosso blog!

Agora, para fixar seus conhecimentos, vamos resolver juntos três exercícios. Dois deles de equação de Bernoulli para fluidos ideais e um exercício para fluidos reais, ou seja, com a consideração da perda de carga no escoamento.

Você pode acompanhar também a resolução das questões acompanhando o vídeo abaixo, que eu preparei para te ajudar!

Os exercícios do post foram baseados em no livro Mecânica dos fluidos de Franco Brunetti. Então, caso você queira se aprofundar sobre o assunto, sugiro que dê uma conferida nesse livro!

Vamos lá?

Exercício 1

A figura abaixo apresenta um sifão. Sabendo que a pressão no ponto S do sifão deve ser maior que – 60 kPa em pressão relativa e desprezando as perdas de carga determine a velocidade da água (\mathrm{{\gamma_a} =10^4 N/m^3}) no sifão e a máxima altura que o ponto S pode ter em relação ao ponto A.

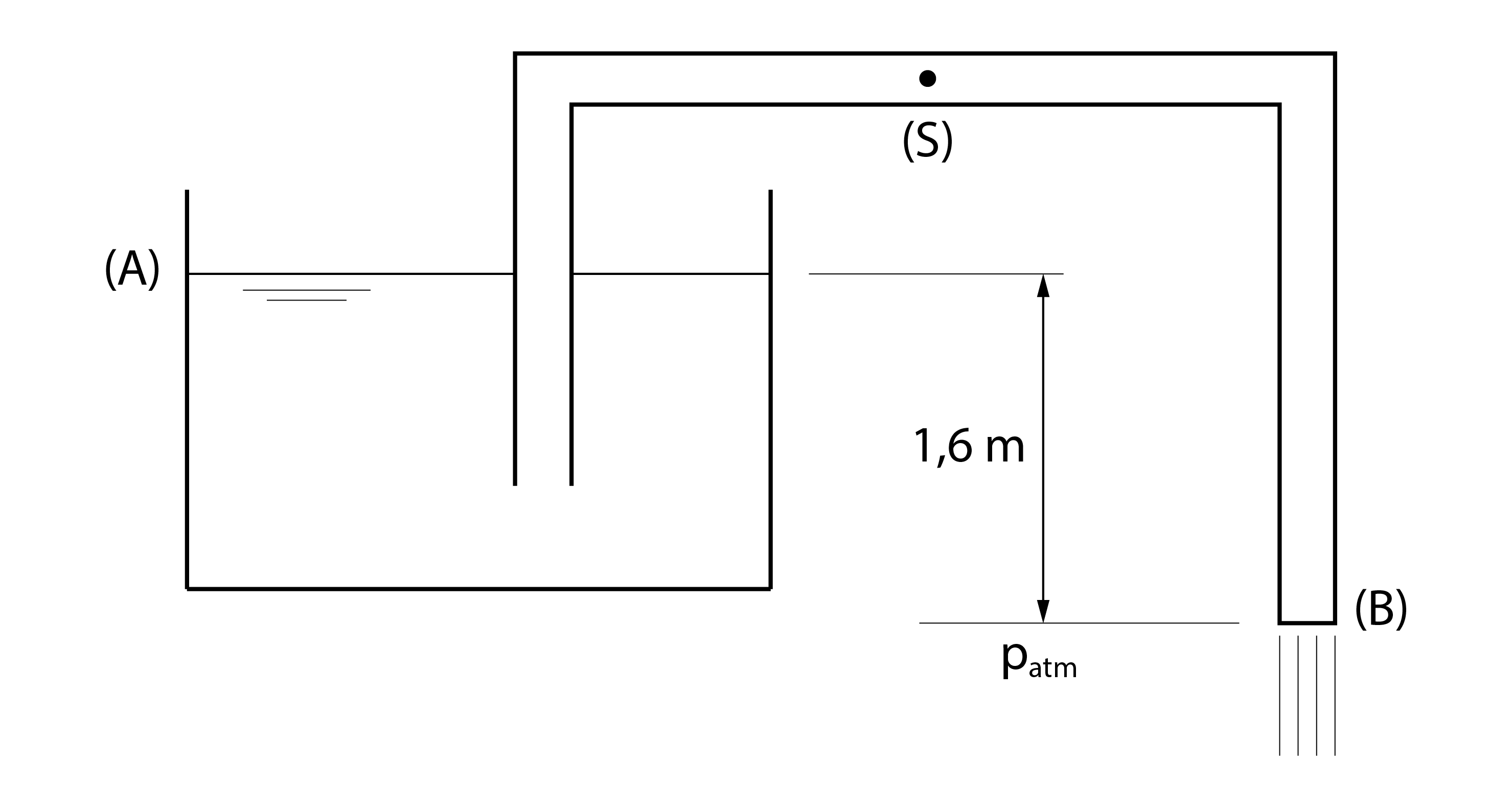
Resolução

Para a resolução da questão, vamos inicialmente determinar a velocidade de fluxo no sifão.

Sabendo que a velocidade de escoamento em todo o sifão é a mesma, podemos utilizar a equação de Bernoulli entre os pontos A e B para determinar tal velocidade. Temos então que:

\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma }}

Como temos que a pressão em ambos os pontos é a própria pressão atmosférica e que a velocidade no ponto A é nula, temos:

\mathrm{{z_A} = \dfrac{{v_B^2}}{{2 \cdot g}}}

\mathbf{{v_B} = 5,66m/s}

Agora que já temos o valor da velocidade do fluxo no sifão, podemos aplicar a equação de Bernoulli entre os pontos A e S.

Como temos que a pressão mínima no ponto S é -60 kPa e considerando agora o plano horizontal de referência passando pelo ponto A, temos:

\mathrm{0 = {z_S} + \dfrac{{5,{{66}^2}}}{{2 \cdot g}} - \dfrac{{60 \cdot {{10}^3}}}{{{{10}^4}}}}

\mathbf{{z_S} = 4,4m}

Exercício 2

Calcule a vazão de escoamento no conduto apresentado na figura abaixo. Dados:

• \mathrm{\gamma _a}: 10 kN/m³;
• \mathrm{\gamma _m} : 70 kN/m³;
• A: 400 cm²;
• p₂: 20 kPa;
• g: 10 m/s².

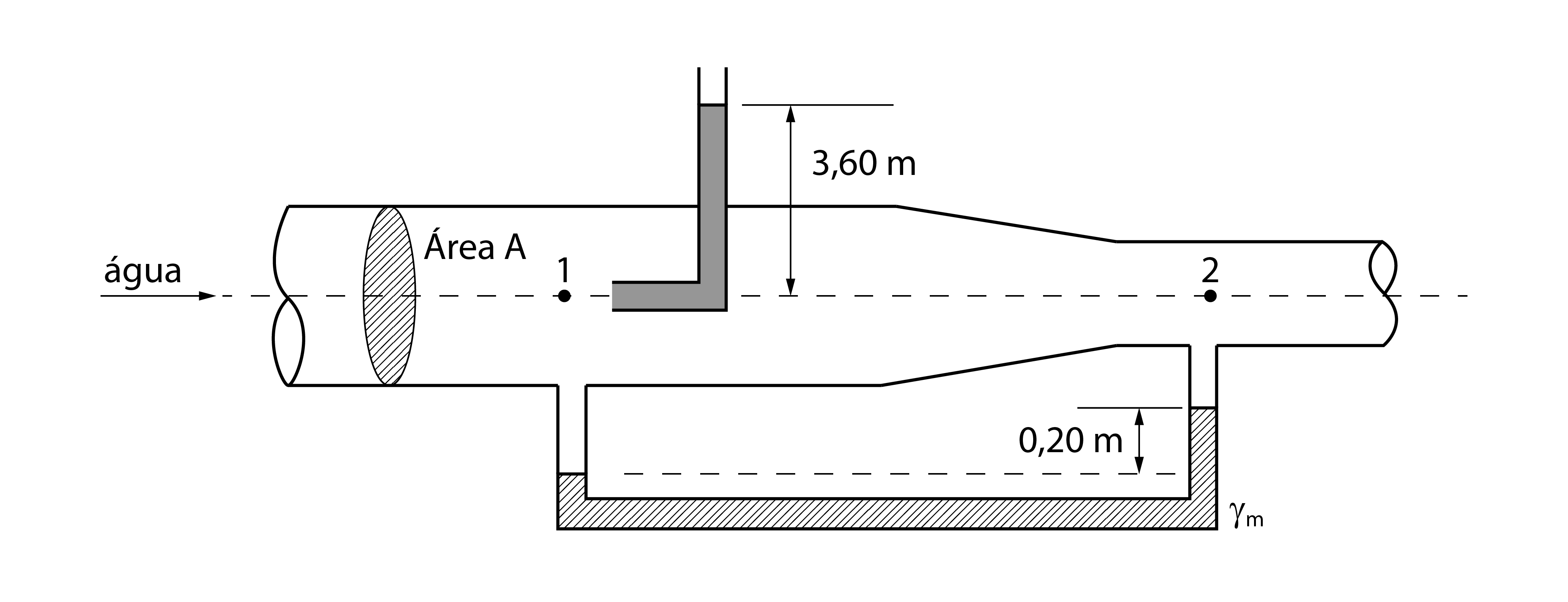
Resolução

Inicialmente, iremos demarcar na figura os pontos notáveis que iremos utilizar durante a questão para mais fácil entendimento no decorrer da mesma.

Os pontos foram escolhidos por serem pontos de mudança de fluido (água e fluido manométrico) ou por serem pontos que se sabe características como velocidade e pressão.

Logo, temos o seguinte esquema:

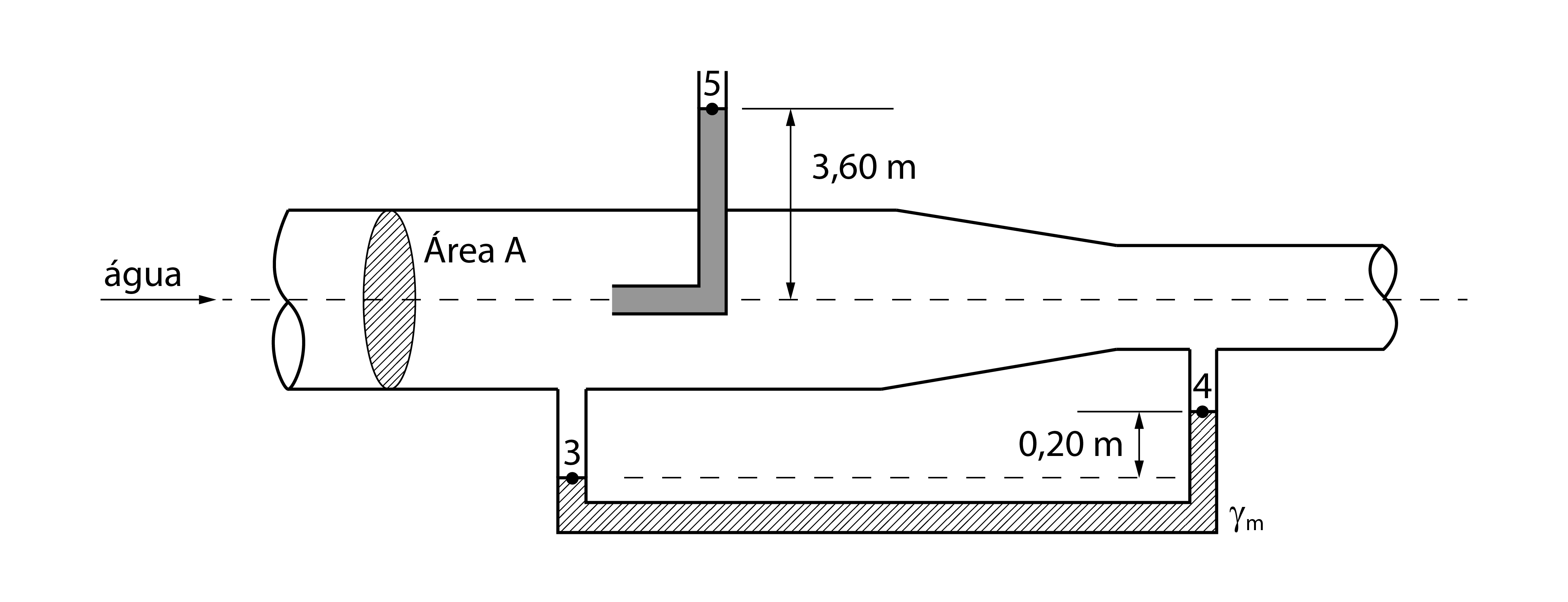
A questão pede que se determine a vazão do escoamento, ou seja, precisamos determinar a velocidade de escoamento.

Então, vamos aplicar a equação de Bernoulli para os pontos 1 e 5 do escoamento. Temos:

\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = {z_5} + \dfrac{{v_5^2}}{{2 \cdot g}} + \dfrac{{{p_5}}}{{{\gamma _a}}}}

Como o ponto 5 possui velocidade nula, nele atua somente a pressão atmosférica e ele encontra-se numa cota 3,60 m acima do ponto 1, podemos desenvolver a equação para:

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}

Como não temos os valores de v₁ e nem de p₁, não conseguimos desenvolver, por ora, tal equacionamento.

Porém, temos um tubo U entre os pontos 1 e 2 e foi dada a pressão no ponto 2, então, podemos utilizar a lei de Stevin entre os pontos 1 e 2 para determinarmos a pressão no ponto1 e, finalmente, chegarmos a velocidade nesse ponto. Para isso, faremos uso dos pontos 3 e 4. Temos então:

\mathrm{{p_3} - {p_1} = {\gamma _a} \cdot h}

\mathrm{{p_4} - {p_3} = - {\gamma _m} \cdot 0,2}

\mathrm{{p_2} - {p_4} = - {\gamma _a} \cdot \left( {h - 0,2} \right)}

Logo, temos que:

\mathrm{{p_2} - {p_1} = - 0,2 \cdot \left( {{\gamma _m} - {\gamma _a}} \right)}

Como foram dados que p₂ é 20 kPa, \mathrm{\gamma _a} é 10 kN/m³ e \mathrm{\gamma _m} é 70 kN/m³, temos:

\mathrm{{p_1} = 32 kPa}

Então, voltando para formulação encontrada no início da questão, temos:

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _a}}} = 3,60m}

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{3,2 \cdot {{10}^4}}}{{10 \cdot {{10}^3}}} = 3,60m}

\mathrm{v_1^2 = 0,4 \cdot 2 \cdot 10}

\mathrm{{v_1} = 2,83m/s}

Logo, a vazão do escoamento será:

\mathrm{Q = {v_1} \cdot A}

\mathrm{Q = 2,83 \cdot 400 \cdot {10^{ - 4}}}

\mathbf{Q = 0,1132{m^3}/s}

Exercício 3

De acordo com a atual norma de instalações hidráulicas prediais, a carga de pressão mínima em um chuveiro deve ser de 1,0 mH₂O. Para o seguinte esquema representativo das instalações de um banheiro, ilustrado na abaixo, determine a mínima altura de água no reservatório para que essa exigência seja cumprida. Dados:

• Perdas de carga linear na tubulação: 0,08 m/m;
• Perda de carga concentrada por joelho 90º: 0,5 m/peça;
• Perda de carga concentrada por Tê de saída lateral: 2,0 m/peça;
• Perda de carga concentrada por registro de gaveta: 1,2 m/peça;
• Despreze as cargas cinéticas;

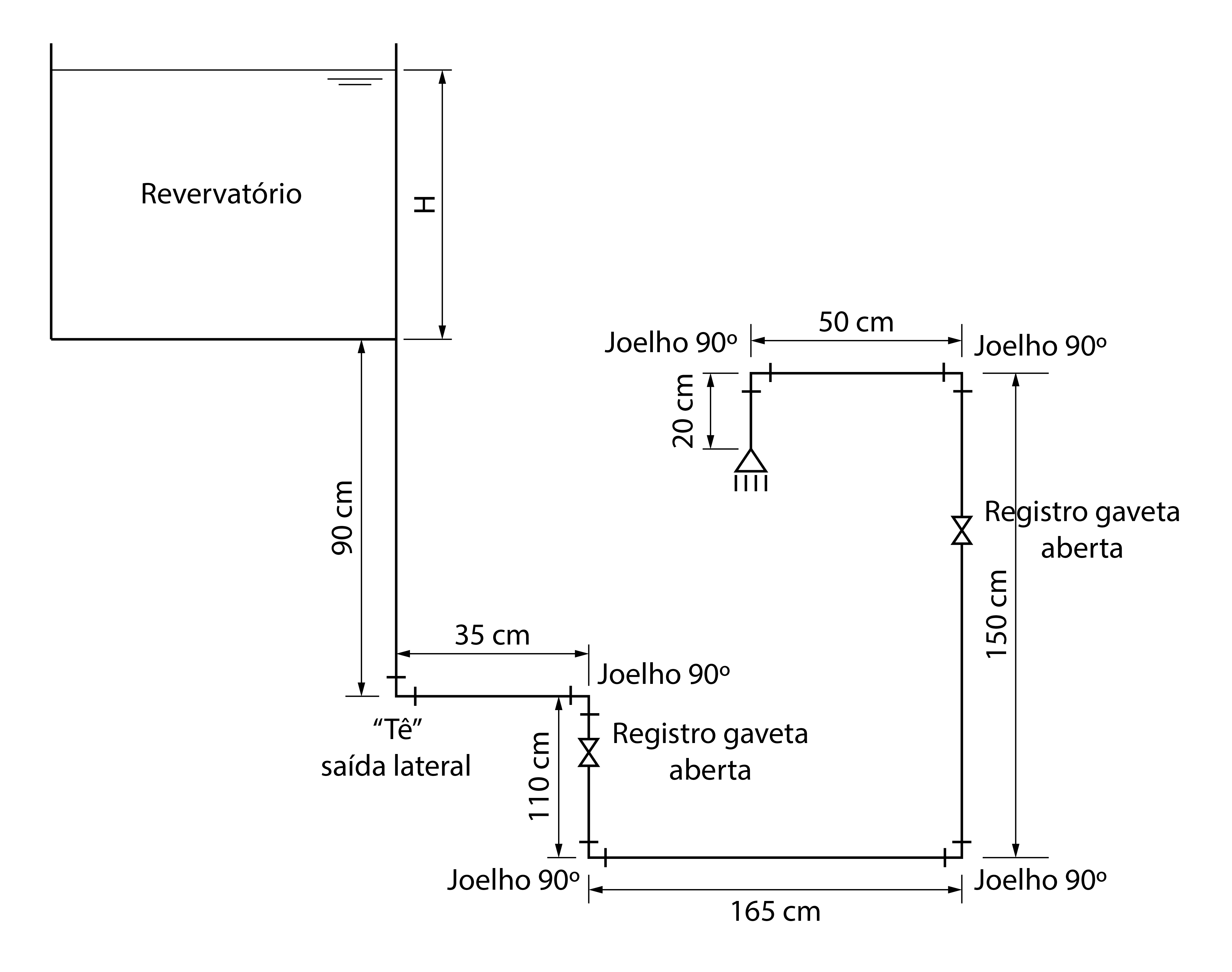
Resolução

Essa questão trata da equação de Bernoulli para fluidos reais, ou seja, deveremos considerar as perdas de carga durante o escoamento do fluido.

Lembrando que a questão já apresenta os valores das perdas de carga distribuídas e pontuais, porém você pode também aprender no nosso blog, como calculá-las.

Para essa questão, iremos utilizar a equação de Bernoulli entre os pontos A e B apresentados na figura acima. Temos então, considerando a perda de carga:

\mathrm{{z_A} + \dfrac{{v_A^2}}{{2 \cdot g}} + \dfrac{{{p_A}}}{\gamma } = {z_B} + \dfrac{{v_B^2}}{{2 \cdot g}} + \dfrac{{{p_B}}}{\gamma } + \Delta H}

Como a questão pede que desconsideremos a carga cinética e afirma que a carga de pressão mínima no chuveiro é de 1,0 mH₂O, temos:

\mathrm{1,10 + 0,90 + h = 1,50 - 0,20 + 1,0 + \Delta H}

\mathrm{h = 0,3 + \Delta H}

Agora, basta calcularmos a perda de carga entre os pontos A e B. Para isso, calcularemos as perdas de carga distribuídas e pontuais. Sabemos que a perda de carga distribuída é 0,08m/m de tubulação.

Somando todo o percurso da tubulação, temos um comprimento de 6,20m, logo a perda de carga distribuída no trecho é:

\mathrm{\Delta {H_d} = 6,20 \cdot 0,08}

\mathrm{\Delta {H_d} = 0,50m}

Para o cálculo das perdas de carga pontuais, devemos somar a perda de carga para cada peça da tubulação:

• 5 joelhos 90º: 5 x 0,5 = 2,5m;
• 1 tê de saída lateral: 2,0m;
• 2 registros de gaveta abertos: 2 x 1,2 = 2,4 m;

Logo, a perda de carga pontual é:

\mathrm{\Delta {H_p} = 6,9m}

A perda de carga total na tubulação é, então:

\mathrm{\Delta H = 6,9 + 0,5 = 7,4m}

Então, o valor de h, para que o chuveiro tenha uma pressão mínima de 1,0 mH₂O é:

\mathbf{h = 0,3 + 7,4 = 7,7m}

Nesse post, através dos exercícios resolvidos, você pode fixar os conteúdos aprendidos nos posts anteriores de equação de Bernoulli e também suas aplicações práticas.

Caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Você pode também entrar no nosso grupo no WhatsApp e conversar com outros profissionais e acadêmicos da área. Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!