Aplicações da Equação de Bernoulli

Agora que você já conhece os conceitos envolvidos na equação de Bernoulli, sua formulação e a diferença entre a equação para fluidos ideais e fluidos reais e o conceito de perdas de carga, apresentaremos algumas aplicações práticas para essa equação.

Neste post você aprenderá sobre o teorema de Torricelli, tubo de Pitot e tubo de Venturi. Vamos lá?

Teorema de Torricelli

O teorema de Torricelli nada mais é do que uma aplicação direta da equação de Bernoulli.

Tal teorema diz respeito ao fluxo de um líquido contido em um recipiente qualquer, através de um pequeno orifício.

Por meio do teorema de Torricelli podemos calcular a velocidade de saída do líquido pelo orifício.

Consideremos então o recipiente mostrado na figura a seguir.

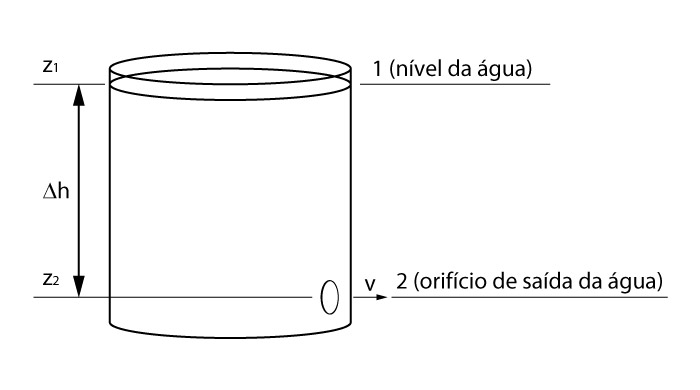
A velocidade de saída no líquido no ponto 2, pode ser calculado aplicando-se a equação de Bernoulli nos pontos 1 e 2.

\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{\gamma } = {z_2} + \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{\gamma }}

Onde:

• z₁ e z₂: distância vertical entre os pontos analisados do fluxo e o plano horizontal de referência;
• v₁ e v₂: velocidade do fluxo nos pontos analisados;
• g: aceleração da gravidade;
• p₁ e p₂: pressão do fluido nos pontos analisados;
• \mathrm{\gamma}: peso específico do fluido analisado.

Sabendo que a velocidade do líquido no ponto 1 é zero, pois o fluido está em repouso no topo do recipiente. E considerando o recipiente aberto, teremos a pressão atmosférica atuando nos pontos 1 e 2, logo temos:

\mathrm{{z_1} + \dfrac{{{p_{atm}}}}{\gamma } = {z_2} + \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_{atm}}}}{\gamma }}

\mathrm{\dfrac{{v_2^2}}{{2 \cdot g}} = {z_2} - {z_1}}

Logo:

\mathrm{v_2 = \sqrt {2 \cdot g \cdot H}}

Então, podemos concluir que quanto maior for a diferença de cotas entre a superfície do líquido no recipiente e o orifício, maior será a velocidade de saída do líquido por tal orifício, como ilustrado na figura a seguir.

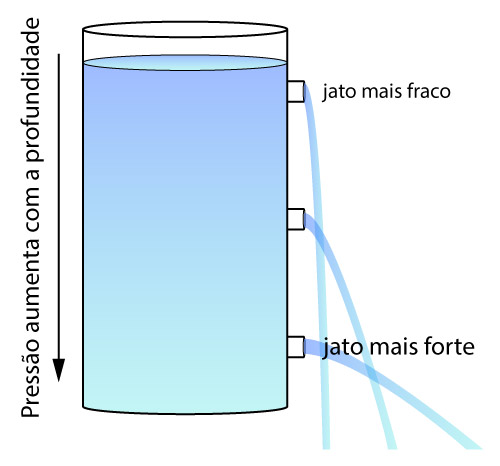
Tubo de Pitot

O tubo de Pitot é um instrumento que tem como finalidade a medição da velocidade de fluidos.

Ele é baseado em modelos físicos e é muito utilizado em laboratórios de hidráulica, aerodinâmica e até mesmo em laboratórios de hidrologia, pois tem função de medir a vazão, através da velocidade, de rios e canais.

Além disso, ainda pode ser encontrado em redes de abastecimento de água, em adutoras e até em aviões, onde é responsável pela mediação da velocidade de escoamento do ar.

Abaixo, apresentamos como funciona internamente um tubo de Pitot e logo depois faremos a demonstração da sua fórmula de utilização por meio da equação de Bernoulli.

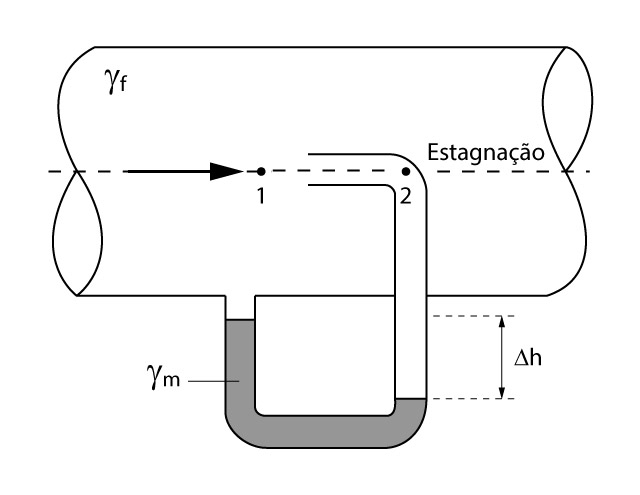
Como ilustrado na figura, o tubo de Pitot é composto por um tubo “U”, com a presença de um líquido manométrico, para calcular a diferença de pressão entre dois pontos do fluxo e assim, determinar a velocidade de escoamento do fluido.

Utilizaremos a equação de Bernoulli para os pontos 1 e 2, já ilustrados na figura anterior.

\mathrm{{z_1} + \dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _f}}} = {z_2} + \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{{{\gamma _f}}}}

Onde:

• \mathrm{{\gamma _f}}: peso específico do fluido que está escoando.

Como ambos os pontos estão na mesma cota, tais valores irão se anular, resultando da seguinte equação.

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _f}}} = \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{{{\gamma _f}}}}

Como o ponto 2 é referente à parede do tubo de Pitot, podemos afirmar que esse é um ponto de estagnação, ou seja, a velocidade do fluido nesse ponto é igual a zero. Logo:

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _f}}} = \dfrac{{{p_2}}}{{{\gamma _f}}}}

\mathrm{v_1= \sqrt {2g \cdot \dfrac{{{p_2} - {p_1}}}{{{\gamma _f}}}}}

Então, agora basta determinarmos a diferença de pressão entre os pontos 1 e 2 para encontrarmos a equação de velocidade do fluido em escoamento através do tubo de Pitot.

Para isso, precisamos lembrar do Teorema de Stevin que afirma que a pressão em um ponto para um fluido estático pode ser calculada apenas com o peso específico do fluido e com a coluna de fluido acima daquele ponto.

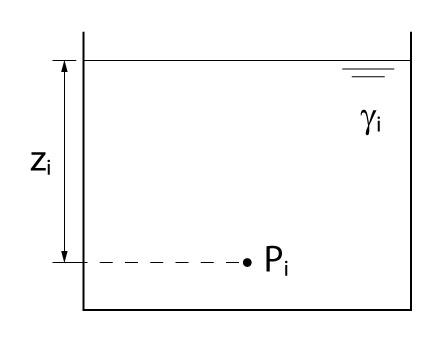
\mathrm{p_i= {\gamma _i} \cdot {z_i}}

Logo, ao analisarmos a situação de pressão para os pontos 1 e 2 para o tubo de Pitot, temos:

\mathrm{{p_2} - {p_1} = \Delta h\left( {{\gamma _m} - {\gamma _f}} \right)}

Onde:

• \mathrm{\gamma _m}: peso específico do fluido manométrico.

Logo, chegamos à conclusão que:

\mathrm{v_1=\sqrt {2g \cdot \dfrac{{\Delta h \cdot \left( {{\gamma _m} - {\gamma _f}} \right)}}{{{\gamma _f}}}}}

Então, podemos perceber mais uma utilização direta da equação de Bernoulli.

Agora falaremos um pouco sobre o tubo de Venturi

Tubo de Venturi

O funcionamento de um tubo de Venturi é bem semelhante à de um tubo de Pito. O tubo de Venturi também tem a finalidade de determinar a velocidade de escoamento de um líquido no interior de uma tubulação.

E assim como o tubo de Pitot, é constituído por um tubo em U com a presença de um líquido manométrico, geralmente o mercúrio, cujos ramos são ligados a segmentos da tubulação com escoamento de fluido.

Um dos ramos é ligado à um segmento normal dessa tubulação e outro ramo é conectado à um estrangulamento, conforme podemos perceber na figura a seguir.

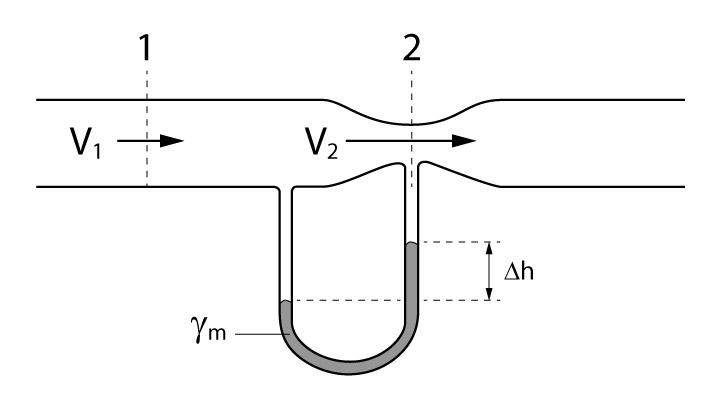
Para dedução da equação para determinação da velocidade no tubo de Venturi, utilizaremos novamente a equação de Bernoulli e o teorema de Stevin, assim como fizemos para o tubo de Pitot.

Fazendo o uso da equação de Bernoulli para os pontos 1 e 2 apresentados na figura anterior e sabendo que ambos estão sob a mesma cota, temos:

\mathrm{\dfrac{{v_1^2}}{{2 \cdot g}} + \dfrac{{{p_1}}}{{{\gamma _f}}} = \dfrac{{v_2^2}}{{2 \cdot g}} + \dfrac{{{p_2}}}{{{\gamma _f}}}}

\mathrm{v_1^2 - v_2^2 = 2g \cdot \left( {\dfrac{{{p_2} - {p_1}}}{{{\gamma _f}}}} \right)}

Fazendo analogia ao tubo de Pitot, podemos calcular uma relação entre p₂ e p₁ utilizando o teorema de Stevin. Temos então:

\mathrm{{p_2} - {p_1} = \Delta h \cdot ({\gamma _f} - {\gamma _m})}

Logo:

\mathrm{v_1^2 - v_2^2 = 2g \cdot \left[ {\dfrac{{\Delta h \cdot ({\gamma _f} - {\gamma _m})}}{{{\gamma _f}}}} \right]}

Agora, pelo princípio da continuidade, sabemos que a vazão do escoamento nos pontos 1 e 2 devem ser iguais, então podemos encontrar uma relação entre v₁ e v₂:

\mathrm{{Q_1} = {Q_2}}

\mathrm{{v_1} \cdot {A_1} = {v_2} \cdot {A_2}}

\mathrm{{v_2} = \dfrac{{{v_1} \cdot {A_1}}}{{{A_2}}}}

Enfim, voltando a equação inicial e substituindo v₂, temos:

\mathrm{v_1^2 - \left( {\dfrac{{v_1^2 \cdot A_1^2}}{{A_2^2}}} \right) = 2g \cdot \left[ {\dfrac{{\Delta h \cdot ({\gamma _f} - {\gamma _m})}}{{{\gamma _f}}}} \right]}

\mathrm{v_1^2\left( {1 - \dfrac{{A_1^2}}{{A_2^2}}} \right) = 2g \cdot \left[ {\dfrac{{\Delta h \cdot ({\gamma _f} - {\gamma _m})}}{{{\gamma _f}}}} \right]}

\mathrm{v_1^2\left[ {1 - {{\left( {\dfrac{{{A_1}}}{{{A_2}}}} \right)}^2}} \right] = 2g \cdot \left[ {\dfrac{{\Delta h \cdot ({\gamma _f} - {\gamma _m})}}{{{\gamma _f}}}} \right]}

\mathrm{{v_1} = \sqrt {\dfrac{{2g \cdot \Delta h \cdot ({\gamma _f} - {\gamma _m})}}{{{\gamma _f} \cdot \left[ {1 - {{\left( {\dfrac{{{A_1}}}{{{A_2}}}} \right)}^2}} \right]}}} }

Chegamos assim, a dedução da formulação para determinação da velocidade de escoamento de um fluido através da utilização de um tubo de Venturi.

 

Concluindo, nest post apresentamos algumas das diversas aplicações práticas da equação de Bernoulli. Percebemos que a mesma tem utilização em diversos ramos da engenharia e principalmente na hidráulica.

No próximo post iremos resolver exercícios da equação de Bernoulli para fluidos ideais e reais e assim, consolidar de vez o aprendizado dessa importante formulação.

Espero que eu tenha te ajudado a sanar suas dúvidas sobre o conteúdo!

Caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Você pode também entrar no nosso grupo no WhatsApp e conversar com outros profissionais e acadêmicos da área. Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!