Vamos fechar o assunto de emenda das armaduras no concreto armado com chave de ouro, colocando a teoria em prática através de um exemplo resolvido.
Nesse exemplo, faremos a verificação de emenda para uma situação hipotética.
Apresentação do problema
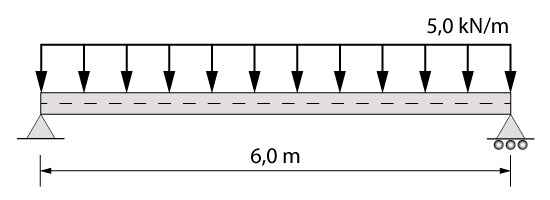
A fim de estudarmos a emendas por traspasse nas armaduras, vamos considerar uma viga de dimensões 20 cm x 50 cm e 6,0 m de vão efetivo. Foi utilizado para mesma concreto C20, ou seja, com resistência característica de 20 MPa e foi considerado a altura útil como 47,5 cm.
Caso você prefira, pode acompanhar a resolução desse exercício através do vídeo abaixo:
Cálculo dos esforços
O primeiro passo é calcularmos os esforços atuantes nessa viga para então calcularmos as armaduras necessárias.
Como se trata de uma viga biapoiada submetida a uma carregamento uniformemente distribuído, podemos aplicar as formulações abaixo:
\mathrm{M_d = \gamma_f \cdot \dfrac{p \cdot {l_{ef}}^2}{8}}
\mathrm{V_d = \gamma_f \cdot \dfrac{p \cdot l_{ef}}{2}}
Substituindo os valores de vão efetivo e carregamento distribuído e considerando \mathrm{\gamma_f = 1,4}, teremos:
\mathrm{M_d = 1,4 \cdot \dfrac{5 \cdot {6}^2}{8} = 31,5 \; kN \cdot m}
\mathrm{V_d = 1,4 \cdot \dfrac{5 \cdot 6}{2} = 21 \; kN}
Dimensionamento das armaduras necessárias
Como não se trata do assunto dessa publicação, nós calcularemos a área de aço de longitudinal e a área de aço transversal através de nossa calculadora de vigas.
Inserindo os dados do exercício para o cálculo da área longitudinal:
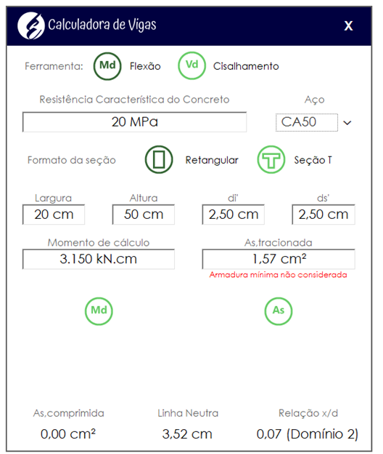
A fim de fornecer uma área de aço de 1,57 cm² podemos utilizar duas barras de 10 mm para a seção.
Utilizando agora o esforço de 21 kN e considerando o Modelo I para o cálculo das armações transversais:
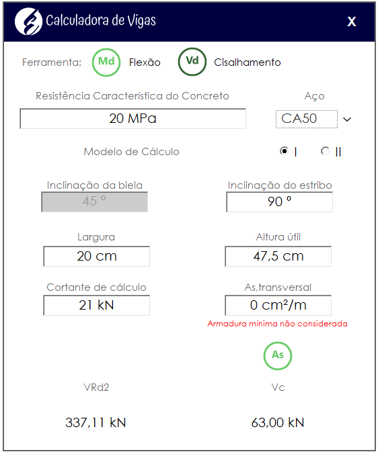
Observe que a calculadora não verifica a armadura mínima. No caso, como \mathrm{V_c > V_d}, a calculadora retornou o resultado zero e seguiremos com a armadura mínima.
\mathrm{A_{sw,min} = \rho_{w,min} \cdot 100 \cdot b_w}
\mathrm{A_{sw,min} = \dfrac{0,09}{100} \cdot 100 \cdot 20 = 1,8 \; cm^2/m}
Para essa área de aço, utilizaremos estribos de 5 mm espaçados a cada 20 cm.
[formulario-calculadora-flexao]Cálculo da emenda por traspasse
Nesse tópico iremos para o cálculo do comprimento de traspasse em si.
Comprimento básico de ancoragem
Vamos aplicar aqui o que aprendemos sobre ancoragem das armaduras no concreto armado. Para isso, vamos lembrar antes a formulação para o comprimento básico de ancoragem:
\mathrm{l_b = \dfrac{\phi}{4} \cdot \dfrac{f_{yd}}{f_{bd}}}
A tensão de aderência de cálculo é calculada pela fórmula abaixo:
\mathrm{f_{bd} = \eta_1 \cdot \eta_2 \cdot \eta_3 \cdot f_{ctd}}
A resistência a tração do concreto, no caso de concretos até 50 MPa e considerando o \mathrm{\gamma_c = 1,4} pode ser calculada pela fórmula abaixo:
\mathrm{f_{ctd} = 0,15 \cdot f_{ck} ^{\frac{2}{3}}}
\mathrm{f_{ctd} = 0,15 \cdot 20 ^{\frac{2}{3}} = 1,11 \; MPa}
Como no caso estamos utilizando barras de CA-50 com diâmetro inferior a 32 mm, utilizaremos \mathrm{\eta_1 = 2,25} e \mathrm{\eta_3 = 1,0}.
Para o valor de \mathrm{\eta_2}, temos que lembrar que para uma viga inferior a 60 cm, os primeiros 30 cm são considerados de boa aderência. Nesse sentido, como nessa publicação iremos verificar apenas a emenda da armadura positiva, consideraremos como uma região de boa aderência e teremos \mathrm{\eta_2 = 1,0}.
Podemos então calcular o valor de \mathrm{f_{bd}}:
\mathrm{f_{bd} = 2,25 \cdot 1,0 \cdot 1,0 \cdot 1,11 = 2,49 \; MPa}
Agora vamos para o cálculo do comprimento básico de ancoragem:
\mathrm{l_b = \dfrac{\phi}{4} \cdot \dfrac{435}{2,49} = 44 \cdot \phi \geq 25 \cdot \phi = 44 \; cm}
Comprimento de ancoragem necessário
Ao passo que já conhecemos o valor do comprimento básico de ancoragem, temos que verificar agora o valor do comprimento necessário de ancoragem. De fato, não teremos muita redução, uma vez que, a área efetiva é praticamente a mesma da área calculada.
\mathrm{l_{b,nec} \geq l_b \cdot \dfrac{A_{s,calc}}{A_{s,ef}}}
\mathrm{l_{b,nec} \geq 44 \cdot \dfrac{1,57}{1,60} = 44 \; cm}
Antes que possamos avançar para a próxima etapa, temos que verificar também o comprimento mínimo de ancoragem.
\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot l_b \\ 10 \cdot \phi \\ 10 \; cm \end{array} \right. }
\mathrm { l_{b,mín} \geq \left\{ \begin{array}{ll} 0,3 \cdot 44 \\ 10 \cdot 1 \\ 10 \; cm \end{array} \right. = 13,2 \; cm}
Assim sendo, seguiremos com o comprimento necessário \mathrm{l_{b,nec} = 44 \; cm}.
Comprimento de traspasse
Por fim, vamos para o cálculo do comprimento de traspasse em si.
A primeira verificação que faremos é a quantidade de barras tracionadas que poderemos emendar em uma mesma seção. Esse valor dependerá do tipo e diâmetro da barra que estamos utilizando, em quantas camadas se distribui a armação e se o carregamento é estático ou dinâmico. A tabela abaixo, retirada da norma, nos fornece o percentual máximo de barras emendadas.
| Tipo de barra | Situação | Carregamento | |
|---|---|---|---|
| estático | dinâmico | ||
| alta aderência | em uma camada | 100% | 100% |
| em mais de uma camada | 50% | 50% | |
| lisa | \mathrm { \phi < 16 \; mm} | 50% | 25% |
| \mathrm { \phi \geq 16 \; mm} | 25% | 25% | |
Nesse sentido, ao distribuirmos as armaduras em uma única camada e como no nosso caso é de um carregamento estático, é possível emendar todas as barras tracionadas em uma mesma seção.
A norma nos fornece a formulação abaixo para o cálculo do comprimento de traspasse:
\mathrm {l_{0t} = \alpha_{0t} \cdot l_{b,nec}}
Assim sendo, precisamos anteriormente obter o fator \mathrm {\alpha_{0t}}, sendo que o mesmo irá variar de acordo com a proporção de barras tracionadas emendadas, seguindo a tabela abaixo:
| Porcentagem de barras emendadas | ≤ 20 % | 25 % | 33 % | 50 % | > 50 % |
| Valores de \mathrm{\alpha_{0t}} | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 |
No nosso caso, como temos as duas armações positivas emendadas, consideraremos \mathrm {\alpha_{0t} = 2,0}. Podemos então calcular o comprimento de emenda por traspasse para as armações positivas:
\mathrm {l_{0t} = 2 \cdot 44 = 88 \; cm}
Armadura transversal na emenda
Para o cálculo da armadura transversal na emenda, eu preparei para você um fluxograma para ficar mais claro como devemos proceder.
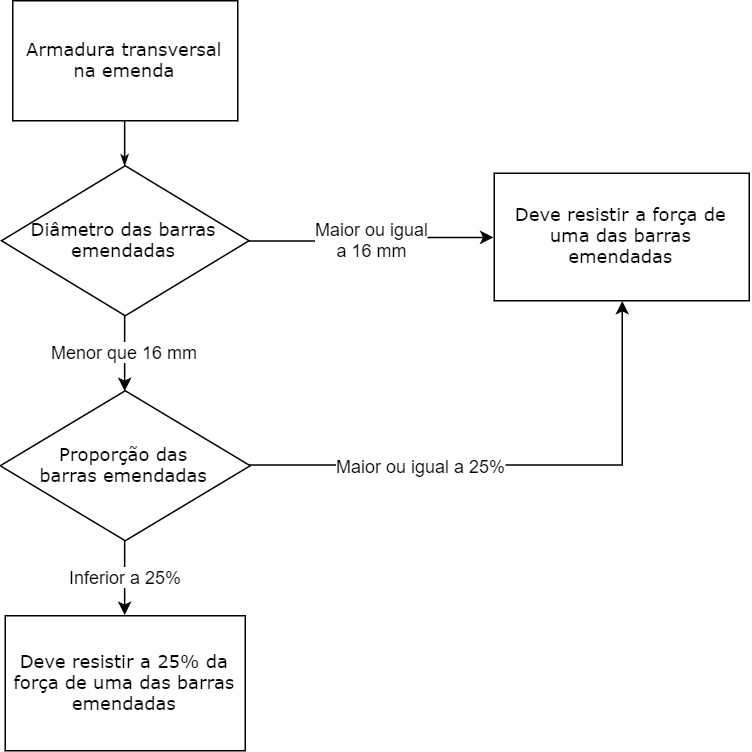
No nosso caso, como a proporção de barras emendadas é superior a 25%, a armadura transversal necessária na região da emenda é a mesma de uma das barras emendadas.
Já que estamos utilizando barras de 10 mm, a armadura transversal na região da emenda deve ser de 0,8 cm². Além disso, conforme ilustra a figura abaixo, essa armação deve ser distribuída nos terços extremos da emenda.
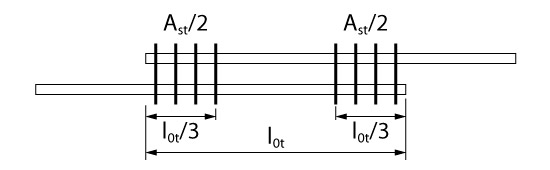
Dessa forma, a área de aço em cada terço de extremidade deve ser superior a \mathrm {0,4 \; cm^2}. Mas lembre-se que essa armação não é adicional a armação de cisalhamento já existente. Ao verificarmos a armação de cisalhamento vemos que a mesma já é suficiente para fornecer essa área de aço transversal para emenda.
Um detalhe é que essa armação transversal deve ter um espaçamento máximo de 15 cm. Assim sendo, cabe a nós decidirmos se utilizaremos esse espaçamento em toda a viga (por questão de facilidade) ou detalharemos esse espaçamento diferenciado na região da emenda.
Recado final
Eu espero que esse conteúdo tenha sido útil para você. Para nos ajudar a continuar distribuindo conhecimento de engenharia compartilhe com seus amigos que possam ter interesse!
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
