Taludes infinitos: exercícios resolvidos

Se você nos segue, sabe que já fizemos um post explicando o que são taludes infinitos e como realizar a análise de estabilidade dos mesmos.

Nesse post, nós resolveremos juntos dois exercícios para fixar o conteúdo estudado anteriormente.

O primeiro exercício será referente a um talude infinito sem percolação de água e o segundo exercício com percolação de água.

Agora, vamos logo aos exercícios!

Exercício 01

Considere o trecho de um talude infinito esquematizado abaixo.

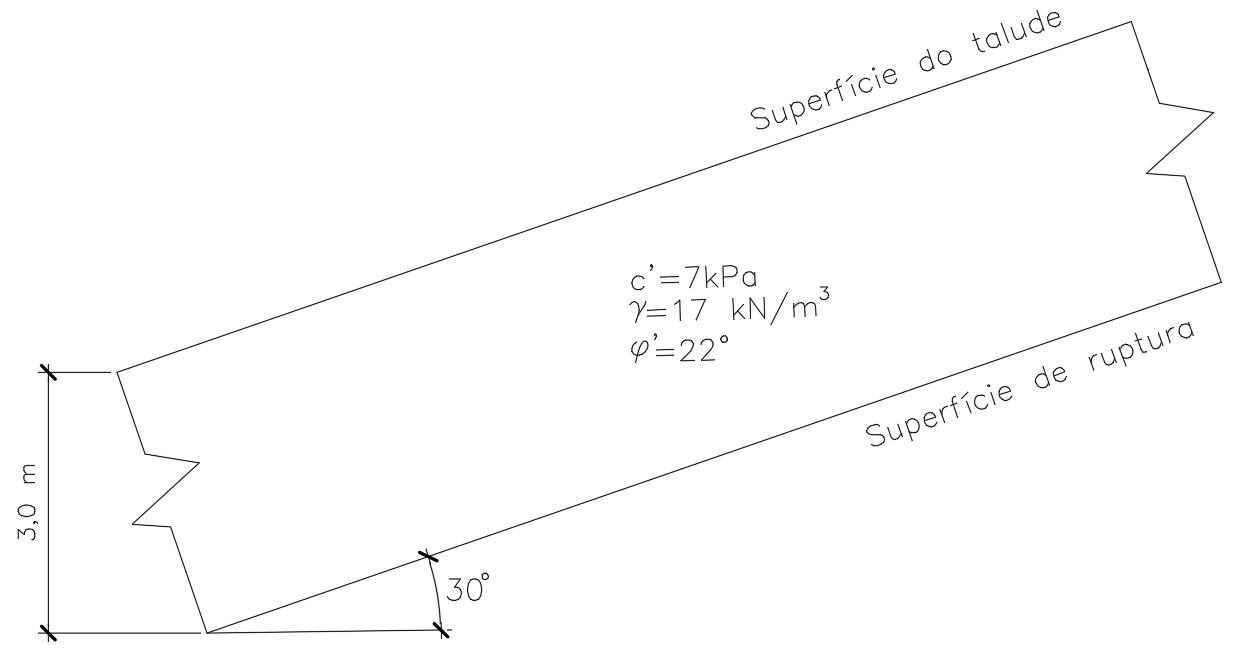
Sobre tal talude, responda:

a) Qual o fator de segurança para o talude apresentado?

b) Qual a máxima espessura que tal talude pode ter para que o mesmo encontre-se na iminência de movimento?

Resolução

Então, para a resolução exercício, nós vamos apenas utilizar a formulação já deduzida no post anterior.

Caso você não visto, recomendo fortemente sua leitura, pois fará você entender como chegamos em cada uma das formulações apresentadas a seguir.

Então, vamos inicialmente calcular o fator de segurança para o talude apresentado. Lembrando que a formulação do fator de segurança para taludes infinitos é:

\mathrm{FS=\dfrac{c^{'}+\gamma\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}{\gamma\cdot H\cdot cos\beta\cdot sen\beta}}

Logo, basta aplicarmos os valores disponíveis no esquema na formulação acima:

\mathrm{FS=\dfrac{7000+17000\cdot 3,0\cdot cos^{2}30º\cdot tan 22º}{17000\cdot 3,0\cdot cos30º\cdot sen30º}}

\mathrm{FS=1,02}

Ou seja, nós podemos dizer que o talude infinito da questão não está seguro, visto que \mathrm{FS=1,02<1,5}.

Mas, a questão também pede que nós determinarmos a espessura do maciço de terra para que o talude esteja na iminência de movimento.

O que isso quer dizer?

Simples, isso apenas quer dizer que a resistência ao cisalhamento desse talude seja exatamente igual à resistência de cisalhamento mobilizada na superfície de ruptura.

Ou seja, FS=1,0. Então, temos novamente a formulação:

\mathrm{FS=\dfrac{c^{'}+\gamma\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}{\gamma\cdot H\cdot cos\beta\cdot sen\beta}}

Perceba que já temos todos os dados do solo. Então, fixando o valor do FS em 1,0, temos que a única incógnita remanescente é o próprio H, que indica a espessura da camada de solo.

Então:

\mathrm{1,0=\dfrac{7000+17000\cdot H\cdot cos^{2}30º\cdot tan 22º}{17000\cdot H\cdot cos30º\cdot sen30º}}

\mathrm{H=3,17m}

Já era esperado que o valor encontrado fosse próximo, porém superior, a 3,0m, que é formato atual do talude, visto que o FS calculado anteriormente foi pouco superior a 1,0m.

Extra

Outro questionamento que poderia ser feito era de qual seria a espessura ideal desse talude infinito a fim de se considerar a segurança do mesmo, ou seja, FS=1,5.

Para isso, usaríamos exatamente o mesmo raciocínio utilizado anteriormente, porém fixando o FS em 1,5. Logo, temos que:

\mathrm{1,5=\dfrac{7000+17000\cdot H\cdot cos^{2}30º\cdot tan 22º}{17000\cdot H\cdot cos30º\cdot sen30º}}

\mathrm{H=1,19m}

Ou seja, chegamos à conclusão que para que possamos atestar a segurança desse talude infinito, a espessura de maciço de solo deveria ser de apenas 1,19m!

Exercício 2

Consideremos o seguinte esquema de um talude infinito com percolação de água apresentado na figura abaixo.

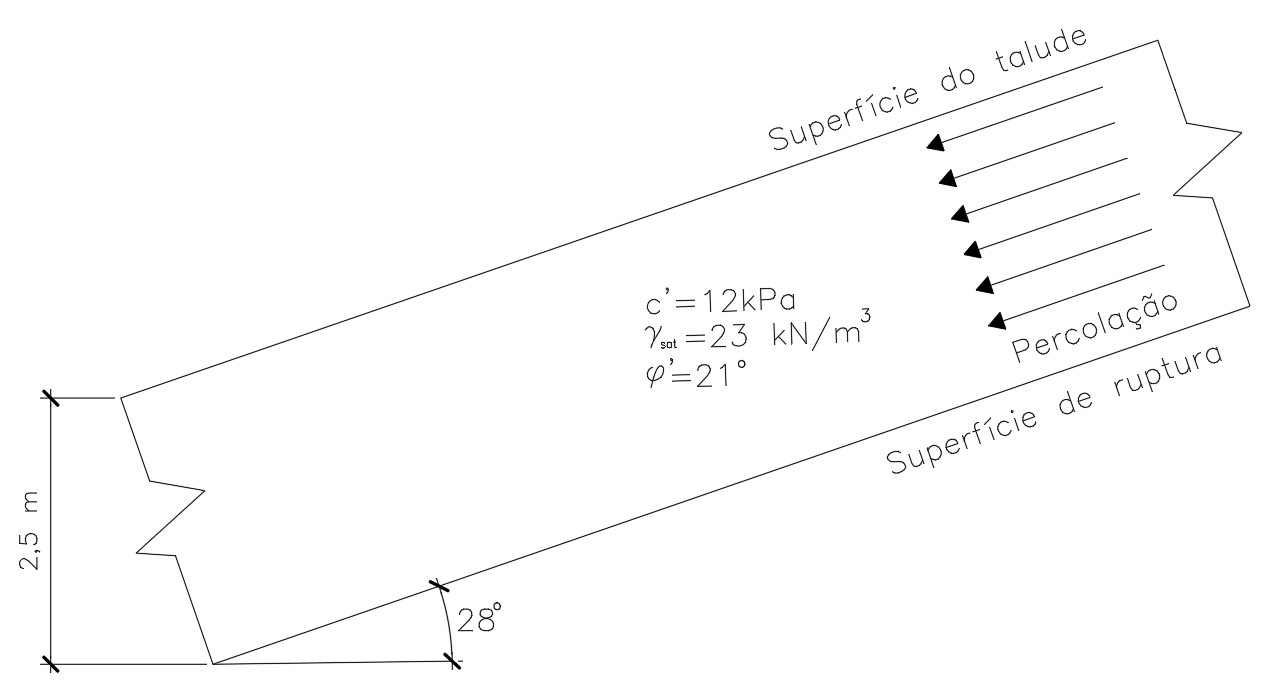
Determine qual  o fator de segurança desse talude infinito e defina se o mesmo é estável ou não.

Resolução

Esse problema é um pouco diferente do anterior, pois aqui há a percolação de água no talude.

Então, como vimos no post anterior, que novamente indico a leitura, para esses casos precisamos entender que a água não mobiliza resistência ao cislhamento.

Partindo desse conceito, conseguimos deduzir a seguinte formulação:

\mathrm{FS=\dfrac{c^{'}+\gamma_{sub}\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}{\gamma_{sat}\cdot H\cdot cos\beta\cdot sen\beta}}

Então, basta aplicarmos diretamente tal formulação para determinarmos o fator de segurança para o talude apresentado.

Lembrando que \mathrm{\gamma_{sub}=\gamma_{sat}-\gamma_{a}}, temos:

\mathrm{FS=\dfrac{12000+13000\cdot 2,5\cdot cos^{2}28º\cdot tan21º}{23000\cdot 2,5\cdot cos28º\cdot sen28º}}

\mathrm{FS=0,91}

Então, encontramos um fator de segurança de 0,91, o que significa que nosso talude não está estável!

Extra

Como exercício extra, poderíamos definir qual seria a espessura de solo do talude para que possamos considerá-lo seguro em projeto, ou seja, FS=1,5.

Temos então que:

\mathrm{1,5=\dfrac{12000+13000\cdot H\cdot cos^{2}28º\cdot tan21º}{23000\cdot H\cdot cos28º\cdot sen28º}}

\mathrm{H=1,15m}

Prontinho!

 

Agora determinamos que para que o talude apresentado no exercício fosse seguro, ele necessitaria ter apenas 1,15m de espessura de solo até a linha potencial de ruptura.

Como você pode perceber com a resolução dessas questões, a análise de estabilidade de taludes infinitos é relativamente simples, mesmo quando há a percolação de água no mesmo!

Eu espero que esse post tenha sido útil e que você tenha aprendido tudo o que tentei passar na resolução dos exercícios.

Porém, se você ainda ficou com dúvida em algo, não se acanhe, coloca aí nos comentários que vai ser um prazer responder você!

Se você preferir, pode dividir sua dúvida ou sugestão conosco no nosso canal do discord!

Além disso, também estamos no Instagram com postagens diárias e no Youtube com vários vídeos semanais para você ficar sempre atualizado do que estamos preparando!

No mais, fico por aqui.

Até uma próxima!