Taludes infinitos: análise de estabilidade

Nesse post você vai aprender tudo sobre a análise de estabilidade de taludes infinitos!

Para o melhor entendimento desse post, recomendo ainda que você dê uma lida no nosso post sobre tipos de deslizamentos de terra e sobre análise de estabilidade de taludes.

Agora, vamos direto ao conteúdo!

Taludes infinitos

São ditos taludes infinitos aqueles que apresentam uma extensão bem maior que sua espessura.

Como já citamos em posts anteriores, a superfície de ruptura de taludes infinitos é linear e paralela à superfície do próprio talude.

Então, uma representação básica de um talude infinito com sua superfície de ruptura é a seguinte:

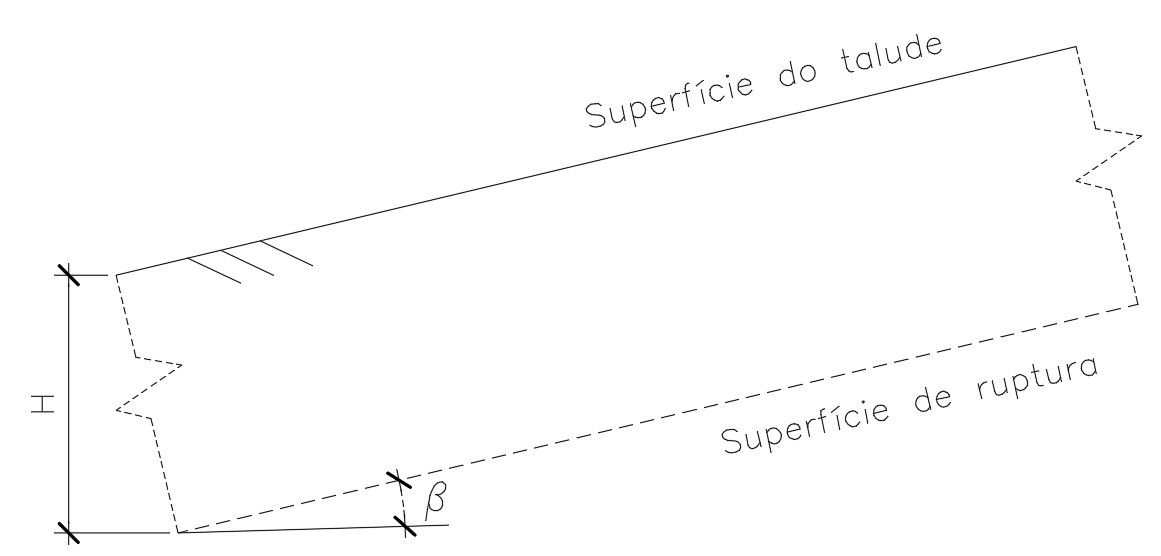
Agora, vamos para a análise da estabilidade desse talude.

Lembrando que, como comentamos em posts anteriores, a análise de estabilidade pode ser feita a partir do cálculo de um fator de segurança.

Tal fator de segurança pode ser calculado como:

\mathrm{FS=\dfrac{\tau_r}{\tau_d}}

Onde:

• \mathrm{\tau_r}: resistência média de cisalhamento do solo;
• \mathrm{\tau_d}: resistência média de cisalhamento desenvolvida ao longo da superfície de ruptura analisada.

Lembrando que vimos também que:

\mathrm{\tau_r=c^{'}+\sigma^{'}\cdot tan\phi^{'}}

Onde:

• \mathrm{=c^{'}}: coesão efetiva do solo;
• \mathrm{sigma^{'}}: tensão normal efetiva;
• \mathrm{\phi^{'}}: ângulo de atrito efetivo do solo;

Então, agora que você já sabe disso, vamos analisar o caso específico de taludes infinitos.

Análise de estabilidade

Então, para que você compreenda melhor cada passo, vamos dividir o cálculo de \mathrm{\tau_r} e \mathrm{\tau_d}.

Vamos inicialmente determinar a tensão média resistente do solo.

Cálculo da tensão de cisalhamento resistente

Como você pode perceber pela formulação apresentada novamente abaixo, tanto a coesão efetiva como o ângulo de atrito efetivo do solo são características próprias do solo, ou seja, apenas a tensão normal efetiva irá variar com variações da geometria do talude.

Então, considere a representação abaixo.

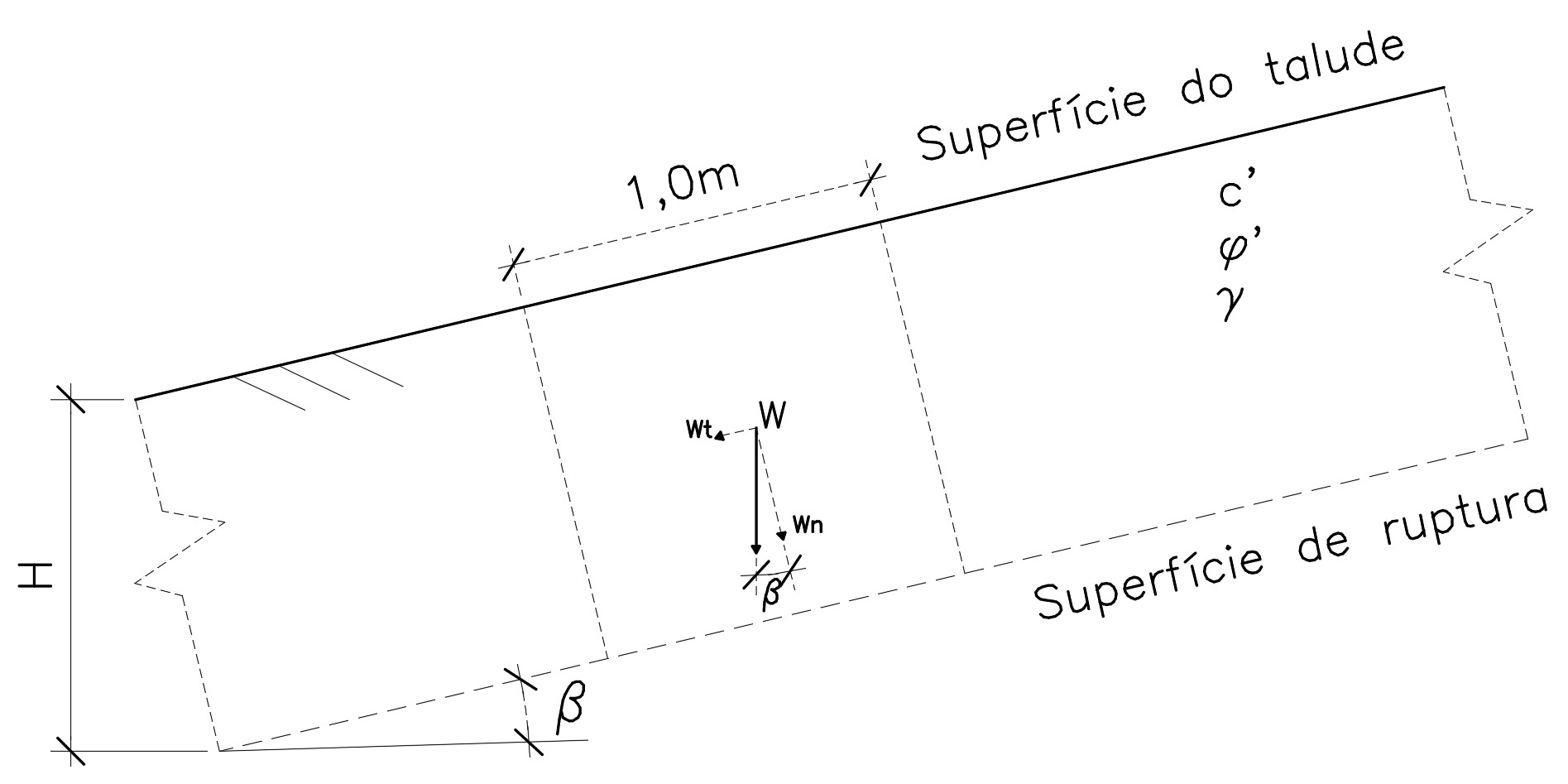
Perceba que, para facilitar a explicação, fizemos a consideração para 1,0m de extensão do talude.

Além disso, perceba que o o peso de solo nessa delimitação (W), pode ser decomposto em uma parcela normal (Wn) e uma parcela tangente (Wt) à superfície de ruptura.

Então, por conceito, a tensão normal efetiva pode ser calculada como:

\mathrm{\sigma'=\dfrac{Wn}{A}}

\mathrm{\sigma'=\dfrac{W\cdot cos\beta}{1*L}}

Onde L representa a dimensão do talude na direção perpendicular a apresentada, ou seja, a largura do talude.

Então, pense bem, o peso de solo W pode ser calculado como o volume de solo multiplicado pelo peso específico do mesmo. Logo temos:

\mathrm{\sigma'=\dfrac{\gamma \cdot 1\cdot H\cdot cos\beta\cdot L\cdot cos\beta}{L}}

\mathrm{\sigma'=\gamma\cdot H\cdot cos^{2}\beta}

Logo, chegamos à conclusão que a tensão de cisalhamento resistente do solo é:

\mathrm{\tau_r=c^{'}+\sigma^{'}\cdot tan\phi^{'}}

\mathrm{\tau_r=c^{'}+\gamma\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}

Cálculo da resistência de cisalhamento desenvolvida na superfície de ruptura

Como partimos da hipótese que o talude está em equilíbrio, a resistência de cisalhamento desenvolvida é igual à tensão de cisalhamento atuante na superfície de ruptura.

Logo, pelo conceito direto de tensão de cisalhamento atuante, temos que:

\mathrm{\tau_d=\dfrac{Wt}{1\cdot L}}

Então, já calculamos anteriormente o valor do peso de solo W. Logo, basta decompor essa força (Wt):

\mathrm{\tau_d=\dfrac{\gamma \cdot 1\cdot H\cdot cos\beta\cdot L\cdot sen\beta}{L}}

\mathrm{\tau_d=\gamma\cdot H\cdot cos\beta\cdot sen\beta}

Pronto, agora que já determinamos a resistência média de cisalhamento e a resistência de cisalhamento desenvolvida ao longo da superfície de ruptura, basta calcularmos o valor do fator de segurança para essa superfície.

Cálculo do fator de segurança

Então, como já vimos anteriormente, o fator de segurança é uma relação entre a resistência ao cisalhamento e o a tensão de cisalhamento atuante ao longo de uma superfície de ruptura.

Portanto, temos que:

\mathrm{FS=\dfrac{\tau_r}{\tau_d}}

\mathrm{FS=\dfrac{c^{'}+\gamma\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}{\gamma\cdot H\cdot cos\beta\cdot sen\beta}}

Pronto! Viu como foi fácil a dedução da fórmula?

Para que você não estranhe, é comum encontrar em alguns materiais e livros a formulação com outra foma, mas é exatamente a mesma formulação!

Então, separando os termos do numerador, você pode chegar à seguinte formulação equivalente à anterior:

\mathrm{FS=\dfrac{c^{'}}{\gamma\cdot H\cdot cos^{2}\beta\cdot tan\beta}+\dfrac{tan\phi^{'}}{tan\beta}}

Então, nós conseguimos, juntos, deduzir a formulação da análise de estabilidade de taludes infinitos.

Porém, perceba que para o caso que analisamos nós desconsideramos qualquer tipo de percolação!

Mas e se tiver percolação no talude? Como podemos considerá-lo?

Cálculo da estabilidade com percolação

Imagine que tenhamos a mesma configuração apresentada anteriormente, porém com percolação de água no nível da superfície do terreno, conforme a figura abaixo.

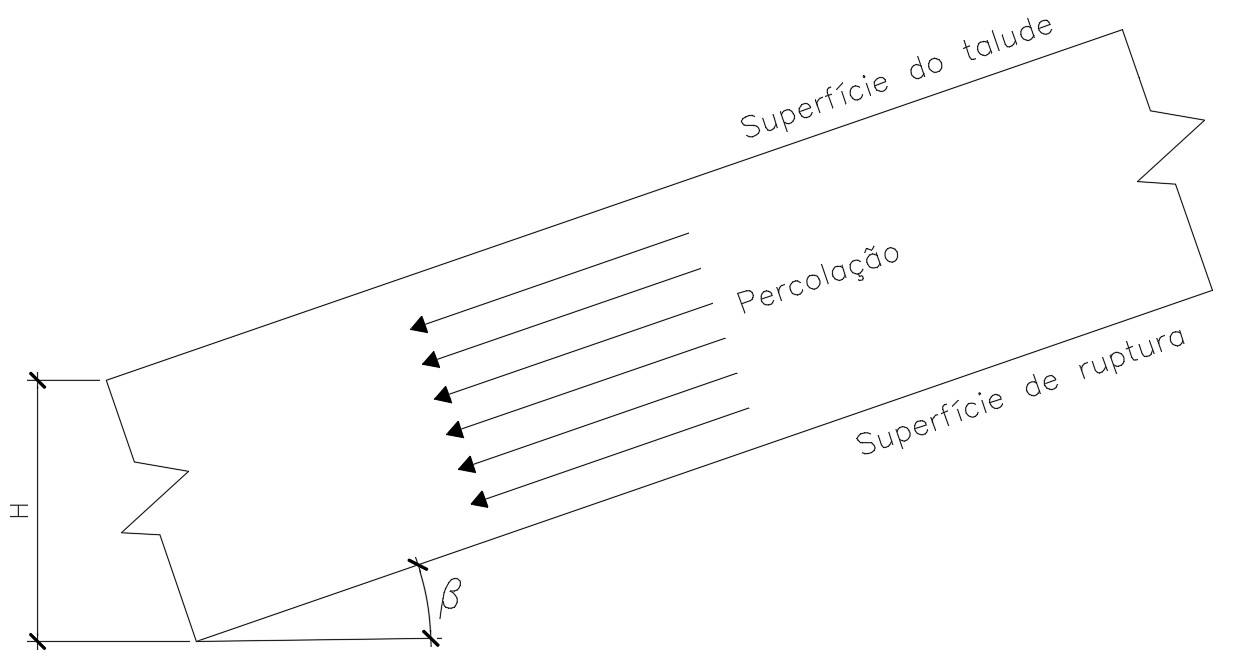
A dedução para a formulação do fator de segurança para esse talude é praticamente idêntica a que realizamos anteriormente.

O que você precisa entender basicamente é que a água não mobiliza resistência ao cisalhamento!

Por isso que utilizamos a tensão normal efetiva para o cálculo da tensão resistente de cisalhamento.

Ou seja, o peso de água “não será considerado” para o cálculo da tensão resistente de cisalhamento.

Entretanto, tal peso de água é considerado para o cálculo da tensão de cisalhamento atuante.

Cálculo da resistência média de cisalhamento

Analogamente ao que fizemos no talude infinito sem percolação, temos que:

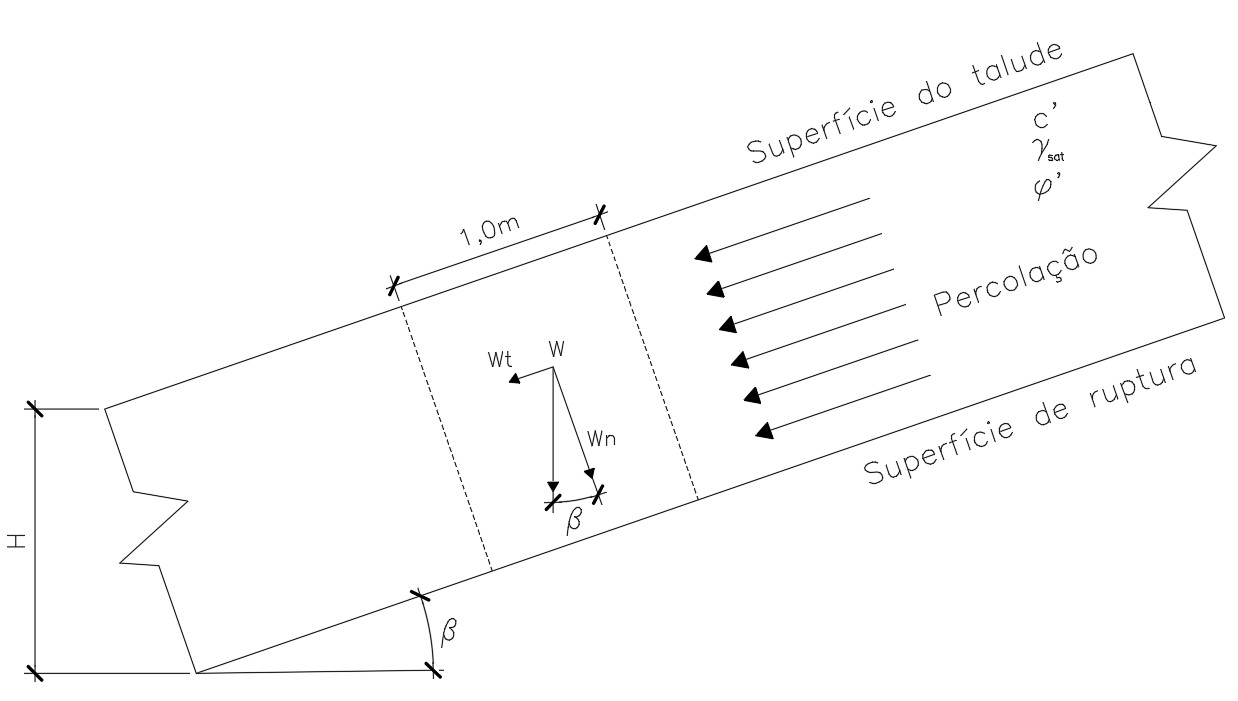
\mathrm{\sigma'=\dfrac{Wn}{A}}

\mathrm{\sigma'=\dfrac{W\cdot cos\beta}{1*L}}

\mathrm{\sigma'=\dfrac{\gamma_{sub} \cdot 1\cdot H\cdot cos\beta\cdot L\cdot cos\beta}{L}}

\mathrm{\sigma'=\gamma_{sub}\cdot H\cdot cos^{2}\beta}

Perceba que estamos utilizando o peso específico do solo submerso, justamente para desconsiderarmos o peso de água na resistência ao cisalhamento! Lembrando que \mathrm{\gamma_{sub}=\gamma_{sat}-\gamma_{a}}.

Logo, temos que:

\mathrm{\tau_r=c^{'}+\gamma_{sub}\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}

Perceba que a formulação é idêntica à encontrada no talude sem percolação, entretanto utilizando o peso específico do solo submerso!

Cálculo da resistência de cisalhamento desenvolvida na superfície de ruptura

Como falamos anteriormente, para o caso da tensão de cisalhamento atuante, devemos considerar sim o peso da percolação de água ao longo do talude.

Logo, teremos a mesma formulação que deduzimos para o talude sem percolação, mas utilizando agora o peso específico do solo saturado.

\mathrm{\tau_d=\gamma_{sat}\cdot H\cdot cos\beta\cdot sen\beta}

Agora, vamos para a determinação do fator de segurança.

Cálculo do fator de segurança

Então, para o cálculo do fator de segurança, basta dividirmos \mathrm{\tau_r} por \mathrm{\tau_d}.

\mathrm{FS=\dfrac{\tau_r}{\tau_d}}

\mathrm{FS=\dfrac{c^{'}+\gamma_{sub}\cdot H\cdot cos^{2}\beta\cdot tan\phi^{'}}{\gamma_{sat}\cdot H\cdot cos\beta\cdot sen\beta}}

Assim como fizemos para o talude infinito sem percolação, vamos apresentar a seguir outra formatação para a mesma formulação, comum de ser encontrada em alguns livros de geotecnia.

\mathrm{FS=\dfrac{c^{'}}{\gamma_{sat}\cdot H\cdot cos^{2}\beta\cdot tan\beta}+\dfrac{\gamma_{sub} tan\phi^{'}}{\gamma_{sat} tan\beta}}

Prontinho! E ficamos por aqui com esse post!

 

Espero que você tenha entendido tudo e que tenha aprendido a fazer a análise e estabilidade de um talude infinito!

Mas caso tenha ficado alguma dúvida, deixa nos comentários que vai ser um prazer te responder.

Então, continue seguindo nosso blog e de nos acompanhar também no YouTube.

Até o próximo post =)