Análise de estabilidade de taludes: conceitos gerais

Se você segue nosso blog, sabe que já falamos sobre o que são taludes e os principais tipos de deslizamentos de terra. Também já falamos sobre soluções para a estabilização de taludes.

Agora, você pode se perguntar: como eu sei se um talude (natural ou não) é estável?

Então, para isso, você terá que fazer a análise da estabilidade do talude.

Nesse post falaremos sobre essa análise, os métodos mais utilizados e, por fim, apresentaremos o conceito de fator de segurança e como calculá-lo.

Então, vamos ao conteúdo!

Análise de estabilidade

Como você deve imaginar, a análise da estabilidade de taludes é uma área de extrema importância na engenharia geotécnica, pois a movimentação de tais maciços de solo podem acarretar grandes perdas materiais e inclusive de vidas.

Então, existem alguns formas de se realizar essa análise da estabilidade de taludes. De maneira geral, podemos subdividi-la em dois grandes tipos:

• Análise probabilística;
• Análise determinística.

Nesse post, abordaremos a análise determinística, que nada mais é do que determinar um fator de segurança para uma possível superfície de ruptura.

Podemos ainda subdividir a análise determinística em três métodos principais:

• Análise limite: se baseia na Teoria da Elasticidade.
• Tensões: tal método se baseia da determinação das tensões em todos os pontos do talude através de métodos numéricos, geralmente MEF (método dos elementos finitos) ou MEC (método dos elementos de contorno).
• Equilíbrio limite: se baseia em determinar a superfície de ruptura crítica, ou seja, aquela com o menor valor do fator de segurança.

Método do equilíbrio limite

Como dito anteriormente, o método do equilíbrio limite permite a determinação do fator de segurança de uma superfície de ruptura do talude.

De maneira bem simplificada, a análise consiste em determinar, para uma certa superfície de ruptura, a resistência média de cisalhamento do talude e a resistência ao cisalhamento desenvolvida (cisalhamento atuante) nessa superfície de ruptura.

De maneira geral, você perceberá que para fazer a análise de estabilidade de um talude nós precisaremos, resumidamente das características geométricas desse talude e dos dados do solo.

Para utilização de tal método, utilizamos as seguintes hipóteses:

• A superfície de ruptura analisada é bem definida;
• O maciço de solo está em condições de ruptura iminente, ou seja um estado de equilíbrio limite, daí o nome do método;
• Para a determinação das tensões resistentes de cisalhamento, utiliza-se o critério de Mohr-Coulomb;
• Assumimos que o critério de ruptura é o mesmo para toda a superfície de ruptura;
• E, por consequência, o fator de segurança calculado deve ser constante ao longo de toda a superfície de ruptura.

Sei que podem parecer muitas informações, mas fique tranquilo, ao longo do post você entenderá que não é nada muito complicado!

Superfícies de ruptura

No que diz respeito à superfície de ruptura, podemos considerar três geometrias principais para essa superfície: ruptura plana, ruptura circular e ruptura com superfície irregular.

O método de análise mais utilizados para superfícies planas em taludes finitos é o método de Culmann, que inclusive é indicado pela norma NBR 5629.

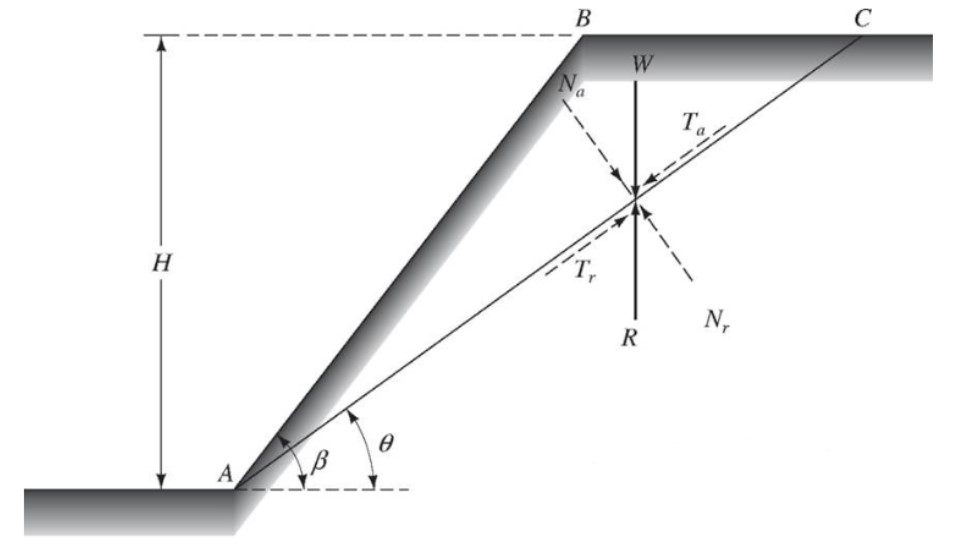
Outro tipo de ruptura de superfície plana comum ocorrem nos chamados taludes infinitos, que nada mais são que taludes que apresentam uma extensão bem maior que sua espessura.

Então, nesse caso, a superfície de ruptura é paralela à própria superfície do talude.

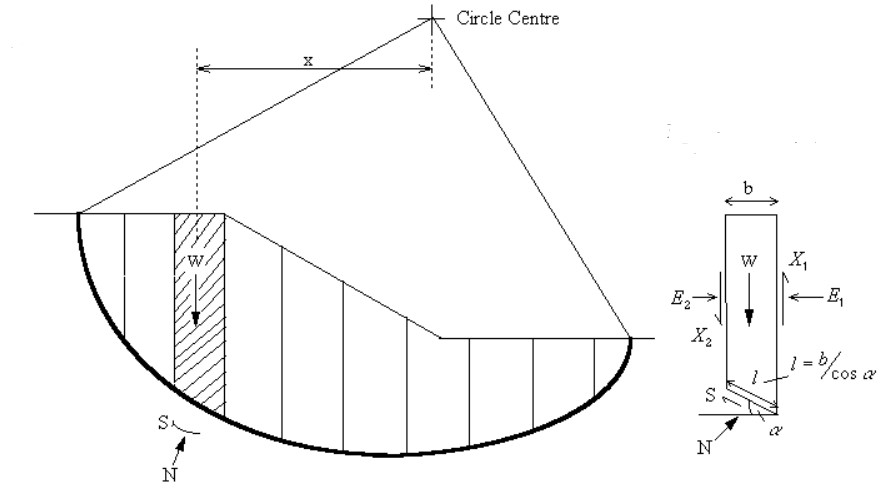
Já para a análise de taludes com superfície de ruptura circular, os métodos mais utilizados são os de Fellenius (método das fatias), o de Bishop e o de Bishop simplificado.

Em posts futuros abordaremos detalhadamente cada um desses métodos.

Por fim, podemos dizer que para a análise de linhas de ruptura com geometria irregular destacam-se os métodos de Janbu, Morgenstern e Price.

Fator de segurança

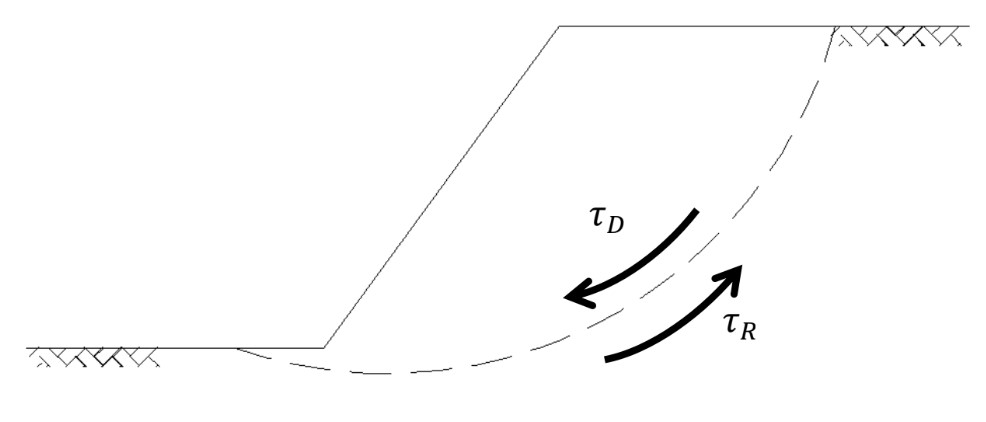
Como já comentamos anteriormente, o fator de segurança é utilizado pelos engenheiros geotécnicos para analisar a estabilidade de um talude. Matematicamente ele pode ser definido como:

\mathrm{FS=\dfrac{\tau_r}{\tau_d}}

Onde:

• \mathrm{\tau_r}: resistência média de cisalhamento do solo;
• \mathrm{\tau_d}: resistência média de cisalhamento desenvolvida ao longo da superfície de ruptura analisada.

Como também já citamos anteriormente, utilizamos o critério de Mohr-Coulomb para a cálculo da resistência de cisalhamento do solo. Logo, temos:

\mathrm{\tau_r=c^{'}+\sigma^{'}\cdot tan\phi^{'}}

Onde:

• \mathrm{=c^{'}}: coesão efetiva do solo;
• \mathrm{sigma^{'}}: tensão normal efetiva;
• \mathrm{\phi^{'}}: ângulo de atrito efetivo do solo;

Então, podemos de maneira análoga, afirmar que:

\mathrm{\tau_d=c^{'}_{d}+\sigma^{'}_{d}\cdot tan\phi^{'}_{d}}

Onde \mathrm{c^{'}_{d}} e \mathrm{\phi^{'}_{d}} são respectivamente a coesão e o ângulo de atrito mobilizados ao longo da superfície de ruptura.

Logo, podemos chegar a seguinte formulação:

\mathrm{FS=\dfrac{c^{'}+\sigma^{'}\cdot tan\phi^{'}}{c^{'}_{d}+\sigma^{'}_{d}\cdot tan\phi^{'}_{d}}}

Então, podemos ainda falar em fator de segurança relativo à coesão (\mathrm{FS_c}) e fator de segurança relativo ao ângulo de atrito (\mathrm{FS_{\phi}}), que são basicamente:

\mathrm{FS_c=\dfrac{c^{'}}{c^{'}_{d}}}

\mathrm{FS_{\phi}=\dfrac{\phi^{'}}{\phi^{'}_{d}}}

Por fim, se você prestar atenção às equações, perceberá que quando \mathrm{FS_c=FS_{\phi}}, temos que elas são iguais ao próprio fator de segurança.

Em relação aos valores do fator de segurança, podemos dizer que:

• FS<1,0: podemos afirmar que o talude está instável.
• FS=1,0: o talude está em equilíbrio limite, na iminência de movimentação;
• FS>1,0: podemos afirmar que para valores superiores a 1,0, o talude é estável.

Na prática são indicados valores de FS>1,5 para elaboração de projetos de taludes estáveis.

 

Pronto, esse foi o conteúdo desse post!

Nos próximos posts falaremos mais especificamente sobre cada um dos métodos de cálculo de estabilidade citados no texto.

Caso tenha ficado alguma dúvida, basta deixar nos comentários que a gente responde.

Então, continue seguindo nosso blog e de nos acompanhar também no YouTube.

Até mais!