Ação do vento em estruturas: exercício resolvido

Agora que você já teve contato com a teoria sobre o cálculo da ação do vento em estruturas, nada melhor que partirmos para um exemplo prático para consolidarmos esse conhecimento. Recomendo que você leia o conteúdo anterior com a teoria antes de avançar nessa publicação.

Apresentação do problema

Nesse exercício, vamos considerar a construção de uma edifício residencial, localizado no estado do Piauí, com dimensões em planta de 20 m por 30m e 18 m de altura, conforme ilustra a figura abaixo.

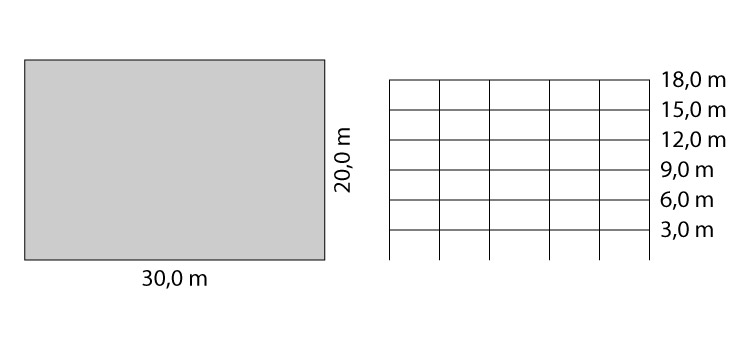
A edificação será construída em Teresina, capital do estado, em terreno fracamente acidentado.

Caso você prefira, pode acompanhar essa resolução também pelo vídeo abaixo:

Velocidade básica do vento

Como já comentado na teoria, a velocidade básica do vento é retirada da imagem com as isopletas presente na norma ABNT/NBR: 6123 (1988). Para facilitar acompanhar essa publicação, repetirei aqui as imagens e tabelas utilizadas durante a teoria.

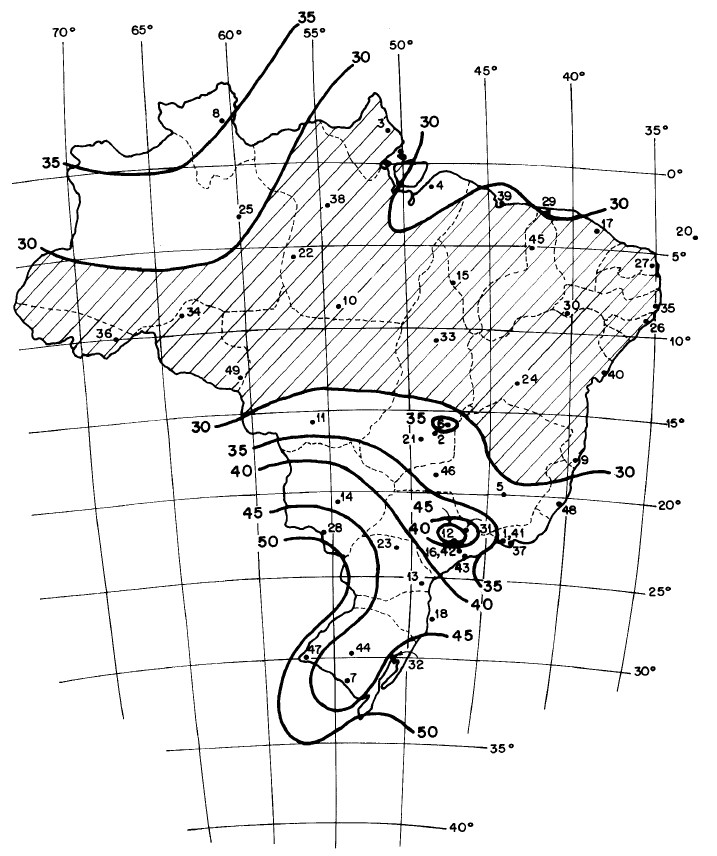
Como todo o estado do Piauí se encontra entre duas isopletas de 30, teremos como velocidade básica do vento \mathrm{V_0 = 30 \; m/s}.

A sua edificação pode estar localizada em uma região encontrada entre isopletas de valores diferentes. Nesse caso, você deve optar ou por utilizar o maior dos valores ou interpolar linearmente os valores encontrados.

Fatores para velocidade característica

Vamos analisar agora os fatores para transformar a velocidade básica (medida em condições iguais em todo o país) para velocidade característica, a fim de adaptar a velocidade básica para a edificação em questão.

Fator topográfico

Como a edificação será executada em um terreno fracamente acidentado, consideraremos o fator topográfico como \mathrm{S_1 = 1,0}.

Fator de \mathrm{S_2}

Vamos analisar primeiro a influência da rugosidade do terreno no fator \mathrm{S_2}. Com a edificação localizada em zona urbana, considerando uma cota média dos obstáculos de 10,0 m, utilizaremos a categoria IV.

Vale chamar atenção que quanto menor a categoria, maior a ação do vento aplicada e, dessa forma, mais a favor da segurança estaremos. Assim sendo, dentro de zonas urbanas, surge a dúvida entre utilizar a categoria IV ou a categoria V. Na dúvida, recomendo utilizar a categoria IV.

Em relação as dimensões da edificação, temos que a maior das dimensões (tanto verticalmente quanto horizontalmente) vale 30,0 m. Assim sendo, classificaremos a edificação como classe B, em que a maior dimensão varia de 20 a 50 m.

Agora que já definimos a categoria do terreno e a classe da edificação, basta entrarmos na tabela fornecida na norma e encontrarmos os valores de \mathrm{b}, \mathrm{p} e \mathrm{F_r}.

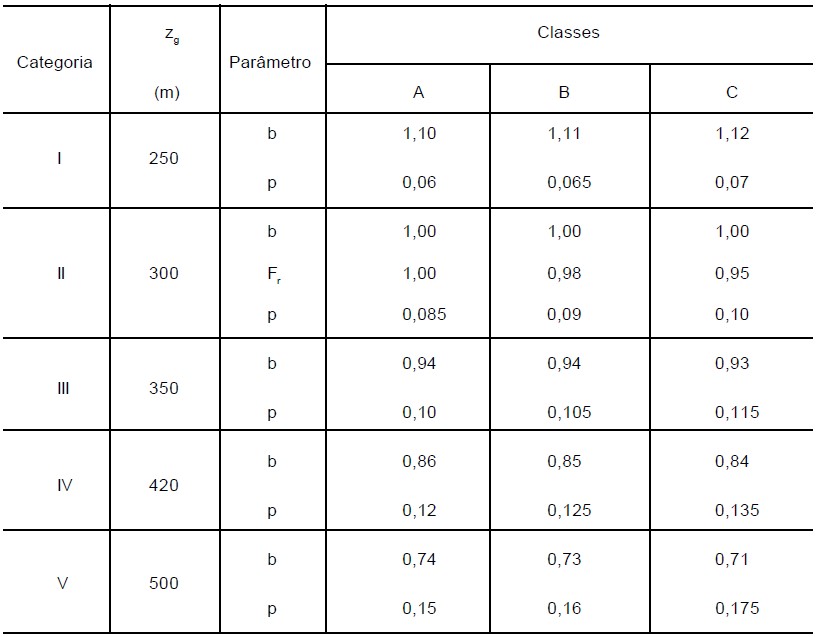
Analisando a tabela, consideraremos \mathrm{b=0,85}, \mathrm{p=0,125} e \mathrm{F_r=0,98}. Observe que, o valor de \mathrm{F_r} sempre é obtido na linha da categoria II, variando apenas com a classe da edificação.

Aplicando agora a formulação de \mathrm{S_2} em relação a cota z, temos:

\mathrm{S_2 = b \cdot F_r \cdot \left( \dfrac{z}{10} \right) ^p}

\mathrm{S_2 = 0,85 \cdot 0,98 \cdot \left( \dfrac{z}{10} \right) ^{0,125}}

Agora vamos aplicar a formulação acima para cada um dos níveis (3, 6, 9, 12, 15, 18):

z (m)	\mathrm{S_2 \; (z)}
		3,0	0,72
6,0	0,78
9,0	0,82
12,0	0,85
15,0	0,88
18,0	0,90

De maneira geral, não teremos problemas com os limites de \mathrm{z_g}, uma vez que são bem superiores a altura dos edifícios usuais.

Fator estatístico

O fator estatístico \mathrm{S_3} depende apenas da utilização da edificação, conforme ilustra a tabela abaixo:

No nosso caso, por se tratar de uma edificação residencial, utilizaremos \mathrm{S_3 = 1,0}.

O entendimento do fator estatístico é simplesmente perceber o dano que o edifício pode causar em múltiplas pessoas caso venha a ruína.

Velocidade característica

Agora que já encontramos a velocidade básica do vento e todos os fatores, podemos obter agora a velocidade característica. Uma vez que calculamos o fator \mathrm{S_2} para cada nível de laje, faremos o mesmo com a velocidade característica do vento. Utilizaremos a seguinte formulação para o cálculo da velocidade característica:

\mathrm{V_k = V_0 \cdot S_1 \cdot S_2 \cdot S_3}

Substituindo os valores que não variam com altura, teremos:

\mathrm{V_k \; (z)= 30 \cdot 1,0 \cdot S_2 \; (z) \cdot 1,0}

\mathrm{V_k \; (z)= 30 \cdot S_2 \; (z)}

Substituindo os valores de \mathrm{S_2} para cada cota, teremos uma tabela contendo a velocidade característica para cada nível:

z (m)	\mathrm{V_k \; (z) \; (m/s)}
		3,0	21,50
6,0	23,44
9,0	24,66
12,0	25,57
15,0	26,29
18,0	26,90

Pressão dinâmica do vento

Por fim, utilizaremos a velocidade característica a cada nível para obtermos a pressão dinâmica atuante em também em cada pavimento. Basta aplicarmos a formulação obtida com o teorema de Bernoulli:

\mathrm{q_{vento} = 0,613 \cdot V_k ^2}

z (m)	\mathrm{q_{vento} \; (z) \; (kN/m^2)}
		3,0	0,28
6,0	0,34
9,0	0,37
12,0	0,40
15,0	0,42
18,0	0,44

A figura abaixo resume as pressões dinâmicas que iremos aplicar em cada nível do nosso edifício:

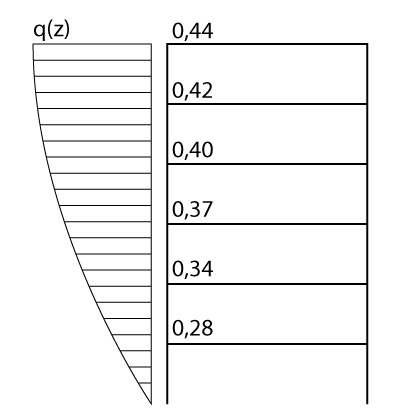
Recado final

Ao final desse post você calculou, na prática, a pressão dinâmica do vento em diversos pavimentos de um edifício residencial localizado no Piauí. O próximo passo é transformarmos essa pressão dinâmica em uma força estática a ser aplicada em nosso modelo estrutural.