A ação do vento deve ser considera mesmo nas estruturas mais simples. Mesmo naquelas de menor porte, em que o vento não tem um efeito preponderante, devemos considerar de modo a respeitar as exigências normativas.
É importante observar que a ação do vento, além do efeitos de primeira ordem, geram deslocamentos horizontais, ocasionando efeitos de segunda ordem. Por isso, seu estudo se torna ainda mais relevante.
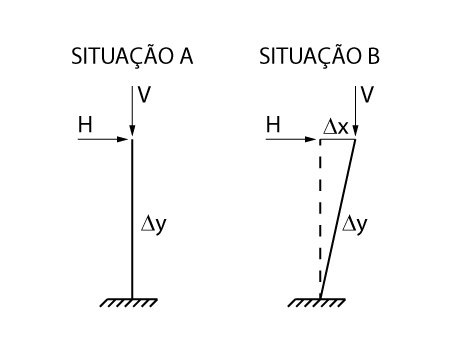
Observe, na figura acima, que antes do deslocamento, o momento fletor na base da peça é gerado apenas pela força horizontal e vale \mathrm{M_0 = H \cdot \Delta y}. Após a deformação, o momento fletor (denominado de momento de segunda ordem) também é influenciado pela ação vertical e vale \mathrm{M = H \cdot \Delta y + V \cdot \Delta x}.
Para começarmos a estudar sobre a ação do vento em estruturas, nessa publicação focaremos na obtenção da intensidade do vento em estruturas.
Considerações iniciais
Devido ao caráter aleatório do vento, é necessário considerar diversas direções de atuação a fim de obter a situação mais desfavorável para a estrutura. As formulações aqui utilizadas foram retiradas da norma ABNT/NBR: 6123 (1988): Forças devidas ao vento em edificações.
Outra consideração importante a ser feita é que esta norma, já publicada há mais de 30 anos, encontra-se no momento em revisão. Dessa forma, é provável que em breve será publicada uma nova versão para a mesma.
Velocidade básica do vento
Com o objetivo de uniformizar a obtenção do vento em todo o país, surge o conceito de velocidade básica do vento. Essa velocidade é basicamente aquela obtida em todo o país de acordo com várias condições de anotação e estatística. São elas:
- Velocidade básica de uma rajada de 3 segundos;
- Probabilidade de 63% de ser excedida pelo menos uma vez dentro do período de retorno de 50 anos;
- Altura de 10 m;
- Terreno plano e sem obstruções.
Com essas regras, temos que a velocidade básica foi obtida em todo o país seguindo as mesmas condições. A figura abaixo, retirada da norma citada acima, apresenta as isopletas (ou seja, curvas de mesmo valor) de velocidades básicas do vento.
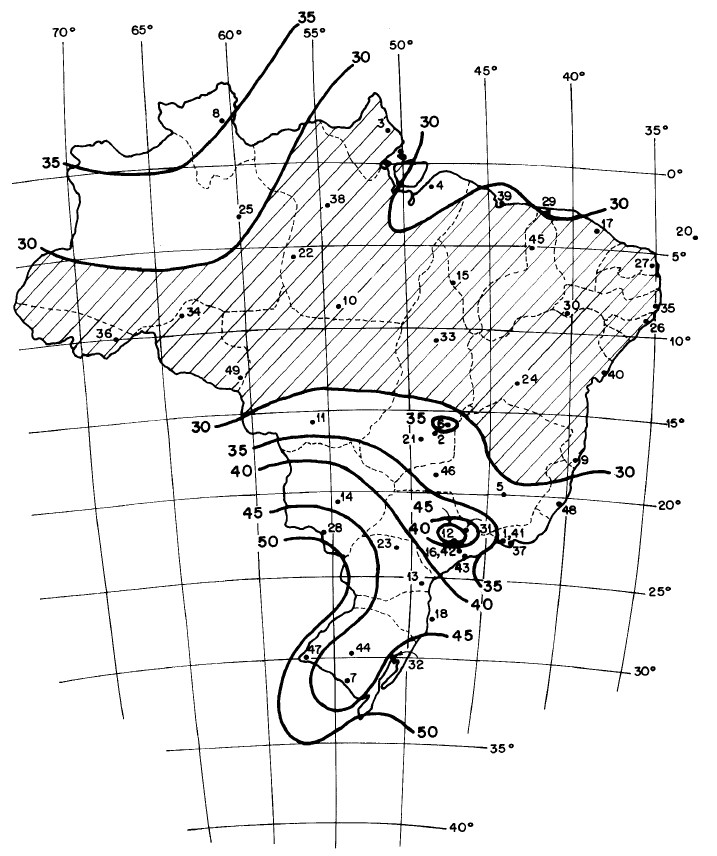
É importante não confundir o valor apresentado ao lado dos pontos com os valores de velocidade básica. Os valores ao lado dos pontos representam apenas a numeração das estações.
Para melhorar a explicação, vamos para alguns exemplos:
- O ponto 45, dentro do estado do Piauí, encontra-se entre duas isopletas de 30. Logo, consideramos como velocidade básica o valor de 30 m/s;
- o ponto 11, dentro do estado do Mato Grosso, encontra-se entre uma isopleta de 30 e uma isopleta de 35. Dessa forma, cabe ao engenheiro optar por utilizar o maior dos dois valores ou realizar alguma interpolação entre esse valores.
Velocidade característica do vento
Agora que já conhecemos o conceito de velocidade básica do vento, vamos aprender o significado de velocidade característica do vento. A ideia é basicamente adaptar a velocidade básica do vento para a sua edificação, variando com as dimensões e finalidade da edificação e a rugosidade do terreno.
A velocidade característica do vento pode ser obtida a partir da formulação abaixo:
\mathrm{V_k = V_0 \cdot S_1 \cdot S_2 \cdot S_3}
Vamos comentar agora cada um dos fatores.
Fator topográfico \mathrm{S_1}
Como o nome indica, é o fator que leva em consideração o relevo do terreno em que a edificação se encontra.
No caso de terrenos planos, teremos o fator como 1,0.
Para região de taludes, temos três pontos para observar:

Para os pontos A e C, consideraremos \mathrm{S_1=1,0}. O ponto C está localizado a uma distância de quatro vezes a altura do talude a partir do ponto B.
No ponto B, o valor de \mathrm{S_1} irá variar de acordo com altura do ponto analisado e também da inclinação do talude.
Caso a inclinação seja igual ou inferior a 3º, consideraremos o terreno como fracamente acidentado e assim utilizaremos o mesmo valor para terrenos planos.
Para inclinações entre 6º e 17º (incluindo os valores de extremidade) iremos utilizar a seguinte formulação:
\mathrm{S_1 (z) = 1,0 + \left( 2,5 - \dfrac{z}{d} \right) \cdot tg \left( \theta - 3 ^{\circ} \right) \geq 1,0}
No caso de inclinações iguais ou superiores a 45º:
\mathrm{S_1 (z) = 1,0 + \left( 2,5 - \dfrac{z}{d} \right) \cdot 0,31 \geq 1,0}
Nos casos intermediários de inclinações entre 3º e 6º e entre 17º e 45º, a norma recomenda interpolarmos linearmente.
Agora que já conhecemos o fator para os pontos A, B e C, podemos interpolar linearmente novamente para obtermos os valores entre os pontos A e B e entre os pontos B e C.
Fator \mathrm{S_2}
O segundo fator é influenciado pela rugosidade do terreno, dimensões da edificação e a altura do ponto analisado.
Rugosidade do terreno
A norma brasileira classifica a rugosidade do terreno em cinco categorias diferentes:
Categoria I: superfícies lisas de grandes dimensões, com mais de 5 km medida no sentido do vento incidente. Alguns exemplos são: lagos e rios, mar calmo e pântanos sem vegetação.
Categoria II: terrenos abertos, com poucos obstáculos isolados, como arvores e edificações baixas. Zonas costeiras planas, pântanos com vegetação rala, campos de aviação, pradarias e charnecas, fazendas sem sebes ou muros são alguns exemplos dessa categoria. A cota média dos obstáculos é igual ou inferior a 1,0 m.
Categoria III: terrenos planos ou ondulados com obstáculos, tais como sebes e muros, poucos quebra-ventos de árvores, edificações baixas e esparsas. Alguns exemplos dessa categoria são granjas e casas de campo, com exceção das partes com matos, fazendas com sebes e/ou muros e subúrbios a considerável distância do centro, com casas baixas e esparsas. A cota média dos obstáculos é igual ou inferior a 3,0 m.
Categoria IV: terrenos cobertos por obstáculos numerosos e pouco espaçados, em zona florestal, industrial ou urbanizada. Zonas de parques e bosques com muitas árvores, cidades pequenas e seus arredores, subúrbios densamente construídos de grandes cidades e áreas industriais plena ou parcialmente desenvolvidas são exemplos dessa categoria. A cota média dos obstáculos é igual a 10,0 m. Também incluiremos nessa categoria os terrenos que não poderem ser inclusos na categoria V.
Categoria V: terrenos cobertos por obstáculos numerosos, grandes, altos e pouco espaçados, como por exemplo: florestas com árvores altas, de copas isoladas, centros de grandes cidades e complexos industriais bem desenvolvidos. A cota média dos obstáculos é igual ou superior a 25,0 m.
Dimensões da edificação
Além da rugosidade do terreno, as dimensões da edificação também afetam o fator \mathrm{S_2}. As edificações foram então divididas em três classes:
- Classe A para toda edificação na qual a maior dimensão horizontal ou vertical não exceda 20 m.
- Todas edificações ou parte de edificações em que a maior dimensão horizontal ou vertical da superfície frontal esteja entre 20 m e 50 m se encontra na classe B.
- Classe C para toda edificação ou parte de edificação para a qual a maior dimensão horizontal ou vertical da superfície frontal exceda 50 m.
Cálculo do fator
Agora que já conhecemos a categoria do terreno e a classe da edificação, vamos obter os valores de \mathrm{b}, \mathrm{F_r} e \mathrm{p} a partir da tabela abaixo, também retirada da norma.
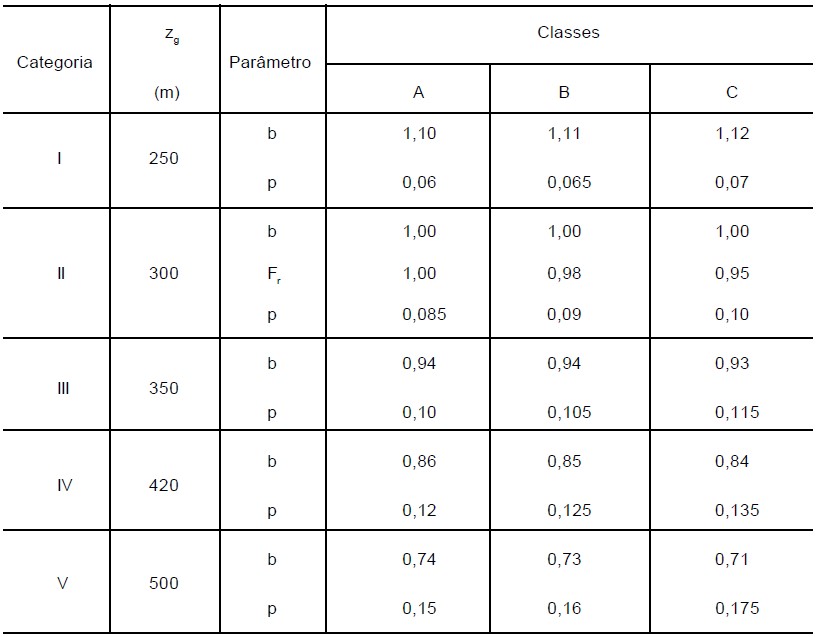
Com os valores retirados da tabela, podemos calcular o fator \mathrm{S_2} a partir da formulação abaixo:
\mathrm{S_2 = b \cdot F_r \cdot \left( \dfrac{z}{10} \right) ^p}
É recomendado calcular um fator diferente para cada altura de pavimento, variando apenas o valor de \mathrm{z}.
O valor de \mathrm{z_g} representa a altura máxima em que a expressão acima é aplicável.
Fator estatístico \mathrm{S_3}
O último fator, denominado de fator estatístico, varia de acordo com a finalidade pra que a edificação foi construída. A norma ABNT/NBR: 6123 (1988) traz uma tabela para os valores do fator \mathrm{S_3}:

Pressão de obstrução
A partir da velocidade característica do vento, podemos calcular a pressão dinâmica \mathrm{q_{vento}} em \mathrm{N / m^2}, a partir da aplicação do teorema de Bernoulli:
\mathrm{q_{vento} = 0,613 \cdot V_k ^2}
A forma de aplicar essa pressão irá variar do tipo de sistema estrutural (concreto armado, alvenaria estrutural, estrutura metálica, etc.) e outra questões como por exemplo: presença ou não de diafragma rígido.
Recado final
Ao final desse post você aprendeu como obter a pressão dinâmica do vento a partir da região do Brasil e características do terreno e da edificação. Dessa forma, essa publicação é uma base para uma sequência de conteúdos futuros sobre ação do vento em estruturas.
Caso prefira, você pode conferir também como calcular a intensidade do vento com um exemplo aplicado.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
