A taxa de ocupação de condutores verticais se trata de um recurso de cálculo alternativo de dimensionamento de instalações de águas pluviais (ou de esgoto) que visa suprimir algumas deficiências trazidas pela ABNT NBR 10.844/89.
O processo de dimensionamento de condutores verticais contido na ABNT NBR 10.844/89, que abrange os escoamentos do tipo vertedouro e orifícios, está sujeito a algumas limitações de cálculo ; sendo, então, necessária a adoção de outros modelos (empíricos ou analíticos) capazes de prevenir contra o escoamento afogado.
A fim de evitar a formação de uma massa hidráulica no condutor vertical e com o intuito de suprir a omissão normativa para diâmetros superiores a 150 mm, adotou-se o dimensionamento dos condutores verticais baseados na limitação da taxa de ocupação.
Taxa de ocupação
Nos trechos de queda (condutores verticais) das instalações de águas pluviais, o escoamento é anelar, isto é, uma lâmina de água escoa pelas paredes do condutor em forma de anel e, no interior deste, há escoamento de ar.
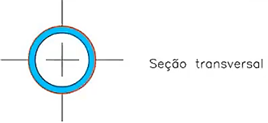
Quando o escoamento por essa seção aumenta, sem os devidos cuidados no dimensionamento, o condutor estará sujeito a um escoamento por seção plena ou afogado. Na iminência desta situação, a instalação poderá sofrer com a formação do chamado “plug hidráulico”, ou até mesmo com situações de pressão negativa.
Assim, o plug hidráulico é uma condição que perturba, sensivelmente, as pressões do ar no interior do sistema, resultando em ruídos indesejáveis e até mesmo no possível colapso de tubulações plásticas de paredes estreitas.
_
Lembre-se de outras patologias comuns em instalações de águas pluviais lendo este artigo.
_
Experimentalmente, foi identificado que a formação desse fenômeno é mais frequente quando a vazão no condutor é tal que o anel hidráulico (escoando junto às paredes do condutor) ocupa uma área de seção entre 1/4 e 1/3 da área da seção transversal da tubulação.
Assim, a capacidade máxima de um condutor vertical pode ser determinada por meio da limitação da taxa de ocupação do líquido na seção transversal do tubo, de modo que se evite a formação do plug.
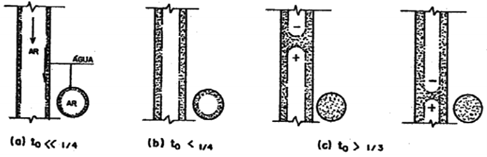
A taxa de ocupação é a fração da seção transversal interna ocupada pela coroa líquida, tal que:
\mathrm{ t_o = \dfrac{Área \ da \ coroa \ líquida} {Área \ da \ seção \ transversal \ interna} }
Ou seja, para que o escoamento anelar seja garantido (sem a ocorrência do fenômeno do plug), devemos garantir que to seja inferior a 1/3 (33,33%). Outras literaturas e normas internacionais costumam utilizar o valor de 1/4 (25%) para que o projeto ganhe uma margem de segurança.
Há, também, a média aritmética entre esses dois valores, ou seja: to = 7/ 24(29,17%).
Portanto, o dimensionamento pela limitação da taxa de ocupação poderá considerar valores de 25%, , 29,17% e 33,33%; em que esses valores representam a porcentagem de fluido que ocupa o condutor vertical.
Velocidade Terminal
Outro conceito importante para a determinação da capacidade máxima de admissão de um condutor vertical de águas pluviais é o da velocidade terminal.
De acordo com Fox, a velocidade terminal é a velocidade de regime permanente que um corpo em queda livre eventualmente atinge. Ou seja, a velocidade de escoamento no condutor será crescente até o momento em que atingirá um valor máximo.
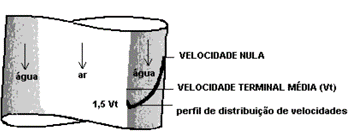
Essa velocidade máxima assume um valor constante após percorrer uma certa extensão do tubo (comprimento terminal), sendo, portanto, a mesma para os demais trechos da queda do tubo de queda . Isso ocorre por conta do equilíbrio alcançado entre a força de atração gravitacional sobre o líquido e o atrito do fluxo líquido com as paredes do tubo.
Por fim, a velocidade terminal pode ser determinada por meio da equação:
\mathrm{ v_t=\dfrac{R_h^{2/3}}{n}}
Onde:
- vt é dado em m/s;
- Rh é o raio hidráulico da coroa líquida;
- n é o coeficiente de Manning.
Taxa de ocupação – Determinação da vazão
Com fundamento nas condições apresentadas anteriormente, a vazão pode ser determinada por meio da equação abaixo:
\mathrm{ Q_d=v_t \cdot A_o}
Sendo vt = Rh2/3/n, então:
\mathrm{ Q_d=\dfrac{R_h^{2/3}}{n} \cdot A_o}
Ainda, o raio hidráulico pode ser determinado pela relação entre a área molhada e o perímetro molhado. Portanto:
\mathrm{Q_d=\dfrac{1}{n} \cdot \left ( \dfrac{Ao}{p_m} \right )^{2/3} \cdot A_o}
\mathrm{ Q_d = \dfrac{1}{n} \cdot \dfrac{A_o^{5/3}}{P_m^{2/3}}}
.
Além disso, por meio da taxa de ocupação, podemos substituir a área ocupada pelo fluido (Ao) por meio da relação to = Ao/A. Portanto:
\mathrm{ Q_d= \dfrac{1}{n} \cdot \dfrac{(t_o \cdot A_o)^{5/3}}{P_m^{2/3}}}
Assim, desenvolvendo a equação da área e do perímetro para um condutor vertical circular, temos:
\mathrm{Q_d = \dfrac{to^{5/3}}{n} \cdot \dfrac{\left ( \dfrac{\pi D^2}{4} \right )^{5/3}}{(\pi D)^{2/3}} }
\mathrm{Q_d= \dfrac{to^{5/3}}{n} \cdot \dfrac{\pi^{(5/3 - 2/3)} \cdot \pi^{(10/3 - 2/3)} } {4^{5/3}} }
\mathrm{Q_d= \dfrac{t_o^{5/3}}{n} \cdot \dfrac{\pi \cdot D^{8/3}}{4^{5/3}} }
\mathrm{Q_d \approx \dfrac{0,312 \cdot t_o^{5/3} \cdot D^{8/3}}{n} }
.
Essa é a equação adotada por algumas literaturas e teses, onde Qd é medido em m3/s e D é medido em metros . Porém, em projetos de instalações de águas pluviais, é comum que façamos o dimensionamento utilizando a vazão medida em L/min.
Assim, inicialmente, vamos converter:
\mathrm{Q_d = \left ( \dfrac{0,312 \cdot t_o^{5/3} \cdot D^{8/3}}{n} m^3/s\right ) \times \left( \dfrac{60.000 \ L/min}{m^3/s} \right ) }
Ainda, lembre-se que o diâmetro utilizado no cálculo está medido em metros. Como comumente adotamos esse valor em milímetros, utilizaremos D = D’/ 1.000:
\mathrm{Q_d = \left ( \dfrac{0,312 \cdot t_o^{5/3} \cdot \left (\dfrac{D'}{1000} \right )^{8/3}}{n} m^3/s\right ) \times \left( \dfrac{60.000 \ L/min}{m^3/s} \right ) }
Portanto,
\mathrm{ Q_d = \dfrac{0,000187 \cdot t_o^{5/3} \cdot (D')^{8/3}}{n}}
Assim, temos as seguintes equações para os determinados materiais:
I) Condutores plásticos (PVC) – n = 0,010:
\mathrm{ Q_d = \dfrac{0,000187 \cdot t_o^{5/3} \cdot (D')^{8/3}}{0,010}}
\mathrm{ Q_d \approx 0,019 \cdot t_o^{5/3} \cdot (D')^{8/3}}
Essa equação é comumente apresentada em textos técnicos, a exemplo do indicado no PCC-USP (2006).
II) Condutores em FoFo novo – n = 0,012:
\mathrm{Q_d = \dfrac{0,000187 \cdot t_o^{5/3} \cdot (D')^{8/3}}{0,012} }
\mathrm{ Q_d \approx 0,0156 \cdot t_o^{5/3} \cdot (D')^{8/3}}
III) Condutores em FoFo usado – n = 0,013:
\mathrm{Q_d = \dfrac{0,000187 \cdot t_o^{5/3} \cdot (D')^{8/3}}{0,013} }
\mathrm{Q_d \approx 0,0144 \cdot t_o^{5/3} \cdot (D')^{8/3} }
Sendo estas, por fim, as equações adotadas em nossa planilha.
Palavras finais
Embora o dimensionamento de condutores verticias de águas pluviais por meio dos ábacos da ABNT NBR 10.844 represente uma solução simplificada, deve-se lembrar que ele não é um método tão conservador quanto o da limitação pela taxa de ocupação.
Além disso, é importante lembrar que o processo de cálculo mostrado neste artigo permite que você adote diâmetros superiores a 150mm, diferentemente dos ábacos.
Por fim, caso tenha interesse em dar início à sua carreira de projetista, indico a você o nosso Curso de projeto de instalações de águas pluviais completo, contento aulas teóricas e práticas de elaboração de um projeto do zero.
Abraços do João!
Engenheiro Civil, ex-Griffon (MWSU), SunDevils (ASU), judoca e pseudo-nadador. Pós-graduando em Gerenciamento de Obras e Tecnologia da Construção.