No post anterior, explicamos quais os procedimentos básicos para realizar o Tratamento por Fatores de Dados de Mercado.
Agora, vamos solidificar o que foi aprendido sobre Avaliação de Imóveis até o momento. Para tanto, propomos um exercício hipotético de uma avaliação de imóvel urbano pelo Método Comparativo Direto de Dados de Mercado, através de tratamento por fatores.
Confira a seguir!
Exemplo prático
Pretende-se avaliar para penhor uma residência localizada na Rua das Abelhas, n º 35, lote 35, quadra A, bairro Jardim São Paulo, na cidade de São Paulo-SP (2ª zona – IF=169,52 R$/m²).
Características complementares do imóvel avaliando:
A edificação possui dois pavimentos, totalizando 200m² de área, está construída em um lote de 250m² (10m de frente e 25m de profundidade), possui padrão econômico de acabamento, estado de conservação necessitando de reparos importantes, idade de 30 anos e a seguinte divisão interna:
- Garagem;
- Sala de estar e sala de jantar;
- Cozinha;
- Área de serviço;
- Banheiro social;
- 4 quartos, sento 3 suítes;
- Varanda.
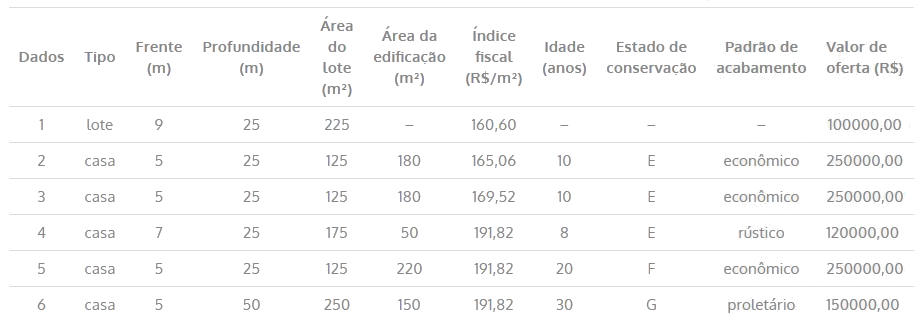
Elementos da amostra do mercado:
RESOLUÇÃO
Passo 01: Escolha dos fatores
A partir dos dados já fornecidos, o primeiro passo para a resolução desse problema é a escolha dos fatores de homogeneização que serão utilizados pelo modelo e, para isso, é imprescindível conhecer as características do imóvel avaliando.
Desse modo, os fatores escolhidos serão:
- Fator oferta, pois os elementos da amostra fornecem apenas o preço de oferta e necessitamos do valor real;
- Fator localização, pois os imóveis da amostra possuem índices fiscais variados;
- Fatores de forma aplicáveis ao terreno, pois os terrenos possuem formas variadas;
- Fator de acabamento, pois os imóveis da amostra possuem padrão de acabamento diferentes entre si;
- Fator de conservação, pois os imóveis da amostra estão em estados de conservação diferentes.
Passo 02: Cálculo dos fatores
Após escolhermos os fatores utilizados no modelo, iremos calculá-los, utilizando como referência os valores fornecidos pela Norma de Avaliação de Imóveis Urbanos de IBAPE de SP, pois é onde o imóvel está localizado.
Fator de oferta
Como não é possível determinar o fator oferta com a informação disponíveis, recomenda-se adotar o valor de 0,90, considerando um desconto de 10% no momento da transação em relação ao valor de oferta.
Fator localização
Esse fator pode ser obtido utilizando a relação entre índices fiscais conforme abaixo:
\mathrm{F_l=\dfrac{IFA}{IFD}}
Dessa forma, temos:
Tabela 1 – Fator localização
| Dados | Índice fiscal (R$/m²) | Fator Localização – Fl |
| 1 | 160,60 | 169,52/160,60=1,056 |
| 2 | 165,06 | 169,52/165,06=1,027 |
| 3 | 169,52 | 169,52/169,52=1,000 |
| 4 | 160,82 | 169,52/160,82=0,884 |
| 5 | 191,82 | 169,52/191,82=0,884 |
| 6 | 191,82 | 169,52/191,82=0,884 |
| Avaliando | 169,52 | 169,52/169,52=1,000 |
Fatores de forma
Tabela 2 – Fatores de forma
| Zonas | Fatores | ||||
| Residencial | Fr | Pmin | Pmáx | f | p |
| 1ª Zona
Residencial Horizontal Popular |
5 | 15 | 30 | Não se aplica | Não se aplica |
|
2ª Zona Residencial Horizontal Médio |
10 | 25 | 40 | 0,2 | 0,5 |
| 3ª Zona
Residencial Horizontal Padrão Alto |
15 | 30 | 60 | 0,15 | 0,5 |
– Fator testada
O fator testada é função exponencial da proporção entre a frente projetada e a frente de referência, pela seguinte expressão:
\mathrm{F_t=\left(\dfrac{F_r}{F_p}\right)^f}
Dessa forma, sabendo que para imóveis localizados na 2ª zona residencial Fr=10m e f=0,2, temos:
Tabela 3 – Fator testada
| Dados | Frente do terreno (m) | Fator Testada – Ft |
| 1 | 9 | (10/9)0,2=1,021 |
| 2 | 5 | (10/5)0,2=1,149 |
| 3 | 5 | (10/5)0,2=1,149 |
| 4 | 7 | (10/7)0,2=1,074 |
| 5 | 5 | (10/5)0,2=1,149 |
| 6 | 5 | (10/5)0,2=1,149 |
| Avaliando | 10 | (10/10)0,2=1,000 |
– Fator profundidade
Esse fator é calculada para cada situação, conforme a seguir:
- Se Pmín ≤ Pe ≤ Pmáx, então \mathrm{F_p=1,00};
- Se 0,5.Pmín < Pe < Pmín, então \mathrm{F_p=\left(\dfrac{P_{mín}}{P_e}\right)^p};
- Se Pe < 0,5.Pmín, então \mathrm{F_p=0,5^p};
- Se Pmáx < Pe < 3.Pmáx, então \mathrm{F_p=\dfrac{1}{(P_{máx}/P_e)+[1-(P_{máx}/P_e)].(P_{máx}/P_e)^p}};
- Se Pe > 3.Pmáx, então \mathrm{F_p=3.P_{máx}}.
Dessa forma, sabendo que sabendo que para imóveis localizados na 2ª zona residencial Pmín=25m, Pmáx=40m, p =0,5, temos:
Tabela 4 – Fator profundidade
| Dados | Profundidade equivalente (m) | Fator profundidade – Fp |
| 1 | 25 | 1,00 |
| 2 | 25 | 1,00 |
| 3 | 25 | 1,00 |
| 4 | 25 | 1,00 |
| 5 | 25 | 1,00 |
| 6 | 50 | 1/[(40/50+(1-40/50)*(40/50)0,5)]=0,344 |
| Avaliando | 25 | 1,00 |
Fator padrão de acabamento
Para esse fator, faremos uso os valores unitários publicados pelo caderno de Valores de Edificações de Imóveis Urbanos do IBAPE/SP para eliminar as diferenças relativas aos detalhes de acabamento entre diferentes imóveis da amostra.
Desse modo, temos:
Fpa,rústico,mínimo=0,409
Fpa,proletário,mínimo =0,624
Fpa,econômico,mínimo =0,919
Fator conservação
Para ajustar as diferenças entre a idade aparente e estado de conservação poderão ser calculados os índices de depreciação, preferencialmente pelo Critério de Ross-Heidecke, conforme a seguinte formulação:
\mathrm{F_{oc}=R+K.(1-R)}
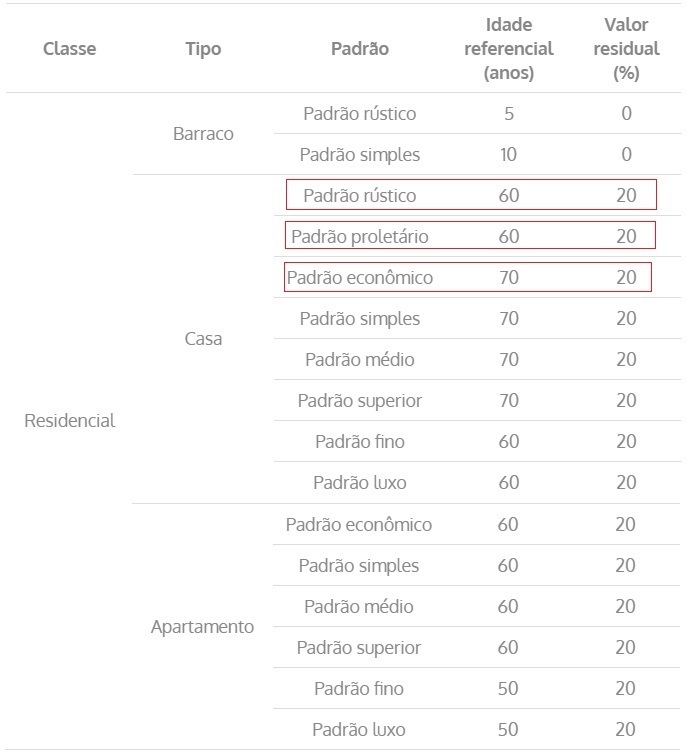
Tabela 5 – Vida referencial e valor residual
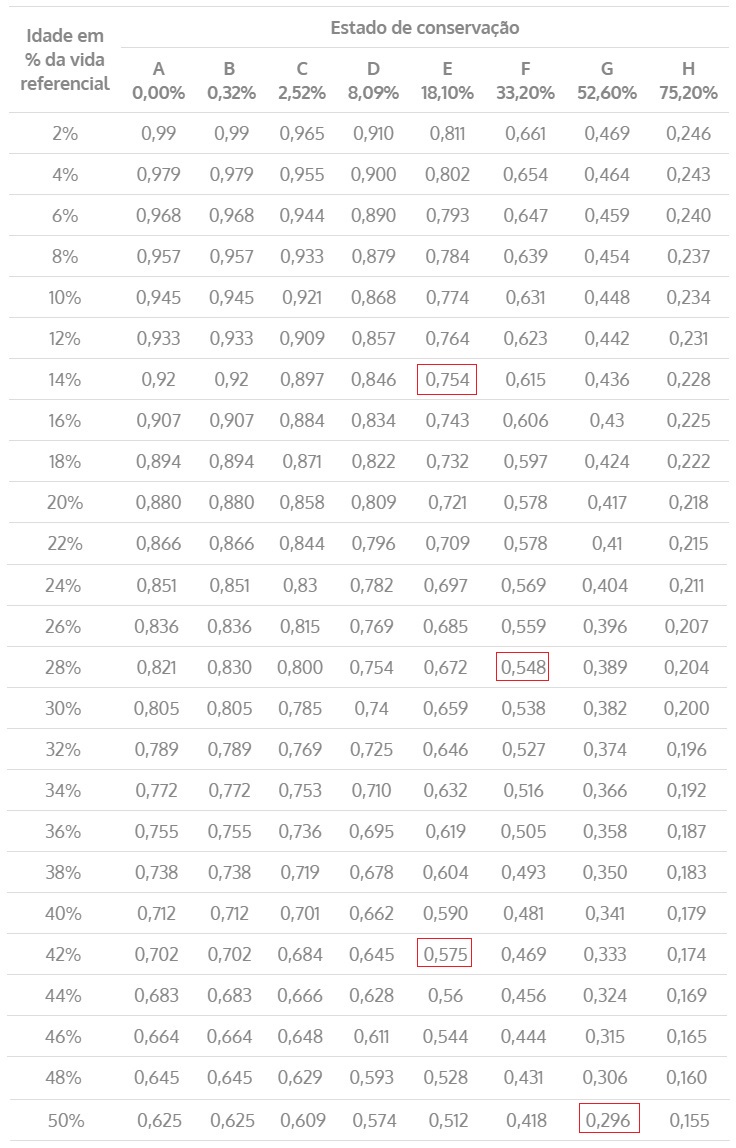
Tabela 6 – Coeficiente de Ross-Heidecke
A partir dos valores fornecidos pela tabela 5, podemos agora calcular o valor da porcentagem de vida em relação à idade referencial dos imóveis:
Tabela 7 – Coeficiente de conservação
| Dados | Padrão de acabamento | Idade real (anos) | Idade referencial
– IR (anos) |
Idade em % da vida referencial |
| 1 | – | – | – | – |
| 2 | Residencial econômico | 10 | 70 | 10/70=14,28% |
| 3 | Residencial econômico | 10 | 70 | 10/70=14,28% |
| 4 | Residencial rústico | 8 | 60 | 08/60=13,33% |
| 5 | Residencial econômico | 20 | 70 | 20/70=28,57% |
| 6 | Residencial proletário | 30 | 60 | 30/60=50,00% |
| Aval. | Residencial econômico | 30 | 70 | 30/70=42,87% |
De posse dos valores das tabelas anteriores, o fator de conservação para os imóveis são:
Tabela 8 – Coeficiente de conservação
| Dados | Idade em % da vida referencial | Estado de conserv. | Valor residual -R | Coeficiente de Ross – K | Fator conservação – Foc |
| 1 | – | – | – | – | – |
| 2 | 14,28% | E | 0,20 | 0,754 | 0,2+0,754(1-0,2)=0,8032 |
| 3 | 14,28% | E | 0,20 | 0,754 | 0,2+0,754(1-0,2)=0,8032 |
| 4 | 13,33% | E | 0,20 | 0,754 | 0,2+0,754(1-0,2)=0,8032 |
| 5 | 28,57% | F | 0,20 | 0,548 | 0,2+0,548(1-0,2)=0,6384 |
| 6 | 50,00% | G | 0,20 | 0,296 | 0,2+0,296(1-0,2)=0,4368 |
| Aval. | 42,87% | E | 0,20 | 0,575 | 0,2+0,575(1-0,2)=0,6600 |
Passo 03: Cálculo do valor das benfeitorias da amostra
De acordo com o tratamento por fatores, o valor de uma edificação pode ser obtida por:
\mathrm{V_c=A_c.CUB.P_{pa}.F_{oc}}
Desse modo, de acordo com o SIDUSCON, sabendo que o custo unitário básico (CUB) de uma residência do tipo multifamiliar de padrão normal em São Paulo é 1.431,53 R$/m², temos:
Tabela 9 – Valor da edificação
| Dados | Área da edificação (m²) | CUB (R$/m²) | Fpa | Foc | Valor da edificação (R$) |
| 1 | – | – | – | – | – |
| 2 | 180 | 1.431,53 | 0,919 | 0,8032 | 190200,72 |
| 3 | 180 | 1.431,53 | 0,919 | 0,8032 | 190200,72 |
| 4 | 50 | 1.431,53 | 0,409 | 0,8032 | 23513,51 |
| 5 | 220 | 1.431,53 | 0,919 | 0,6384 | 184770,02 |
| 6 | 150 | 1.431,53 | 0,624 | 0,4368 | 58527,36 |
Passo 04: Cálculo do valor dos terrenos da amostra
Para encontrarmos o valor remanescente referente ao terreno dos imóveis da amostra, aplicaremos o fator de oferta de 0,90 sobre o preço de oferta e encontraremos o valor negociado, conforme abaixo:
Tabela 10 – Valor do terreno
| Dados | Valor de oferta (R$) | Valor negociado (R$) | Valor da edificação (R$) | Valor do terreno (R$) |
| 1 | 100000 | 90000 | – | 90000,00 |
| 2 | 250000 | 225000 | 190200,72 | 34799,28 |
| 3 | 250000 | 225000 | 190200,72 | 34799,28 |
| 4 | 120000 | 108000 | 23513,51 | 84486,49 |
| 5 | 250000 | 225000 | 184770,02 | 40229,98 |
| 6 | 150000 | 135000 | 58527,36 | 76472,64 |
Passo 05: Aprimoramento da amostra
Após a homogeneização dos dados, o próximo passo é o saneamento da amostra, que consiste na utilização da estatística para eliminar eventuais discrepâncias que podem comprometer a amostra.
Cálculo da média dos valores unitários homogeneizados dos elementos da amostra
Para isso, primeiro precisamos realizar a homogeneização de cada elemento, individualmente, pela expressão abaixo e, após isso, calcular a média aritmética normalmente.
\mathrm{V_u=V_r\cdot[+(F_1-1)+(F_2-1)+(F_3-1)+...+(F_n-1)]}
Tabela 11 – Valores unitários homogeneizados
| Dados | Valor do terreno (R$) | At (m²) | Vr (R$/m²) | Fl | Ft | Fp | Vu (R$/m²) |
| 1 | 90000,00 | 225 | 400,0 | 1,056 | 1,02 | 1,0000 | 430,40 |
| 2 | 34799,28 | 125 | 278,4 | 1,027 | 1,15 | 1,0000 | 327,68 |
| 3 | 34799,28 | 125 | 278,4 | 1,000 | 1,15 | 1,0000 | 320,16 |
| 4 | 84486,49 | 175 | 482,8 | 0,884 | 1,07 | 1,0000 | 460,59 |
| 5 | 40229,98 | 125 | 321,8 | 0,884 | 1,15 | 1,0000 | 332,74 |
| 6 | 76472,64 | 250 | 305,9 | 0,884 | 1,15 | 0,3440 | 115,74 |
Tabela 12 – Média amostral
| Dados | Vu (R$/m²) | Média (R$/m²) | Desvio padrão (R$/m²) |
| 1 | 430,40 | 331,20 | 120,99 |
| 2 | 327,68 | ||
| 3 | 320,16 | ||
| 4 | 460,59 | ||
| 5 | 332,74 | ||
| 6 | 115,63 |
Para esse passo, vale observar que o dado 6 não está contido no intervalo \mathrm{0,5.\overline{x}<V_u<2.\overline{x}}, isso nos mostra que a amostra não é satisfatória, então deveremos eliminar esse dado discrepante.
Verificação pelo critério excludente de Chauvenet
O saneamento da amostra também pode ser feito utilizando o critério excludente de Chauvenet para pequenas amostras.
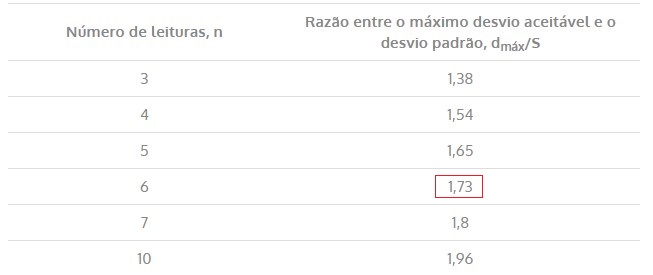
Para isso, os valores críticos da amostra serão calculados conforme equação abaixo e depois serão comparados com o valor crítico determinado pela tabela 13.
Tabela 13 – Critério de Chauvenet para rejeição de valor medido
\mathrm{R_{inf}=\dfrac{\overline{x}-x_{mín}}{S}=\dfrac{331,20-115,63}{120,99}=1,782>1,73}
\mathrm{R_{sup}=\dfrac{x_{máx}-\overline{x}}{S}=\dfrac{460,59-331,20}{120,99}=1,069<1,73}
Conforme observado, o valor de Rinf é superior ao valor crítico para 6 elementos 1,73, logo a amostra é insatisfatória e a média amostral não poderá ser usado para representar o valor homogeneizado do terreno avaliando, conforme constatamos anteriormente.
Desse modo, repetiremos o passo 05 novamente retirando o dado 06.
Tabela 14 – Média amostral (2ª tentativa)
|
Dados |
Vu (R$/m²) |
Média (R$/m²) |
Desvio padrão (R$/m²) |
|
1 |
430,40 |
374,31 |
66,00 |
|
2 |
327,68 |
||
|
3 |
320,16 |
||
|
4 |
460,59 |
||
|
5 |
332,74 |
Dessa vez todos os valores estão no intervalo \mathrm{0,5.\overline{x}<V_u<2.\overline{x}}.
Fazendo a verificação pelo critério de Chauvenet:
\mathrm{R_{inf}=\dfrac{\overline{x}-x_{mín}}{S}=\dfrac{374,31-320,16}{66,00}=0,820<1,65}
\mathrm{R_{sup}=\dfrac{x_{máx}-\overline{x}}{S}=\dfrac{460,59-374,31}{66,00}=1,307<1,65}
Isso mostra que agora a amostra é satisfatória e média de R$ 374,31/m² poderá ser usada para representar o valor homogeneizado do terreno avaliando.
Passo 06: Cálculo do intervalo de confiança
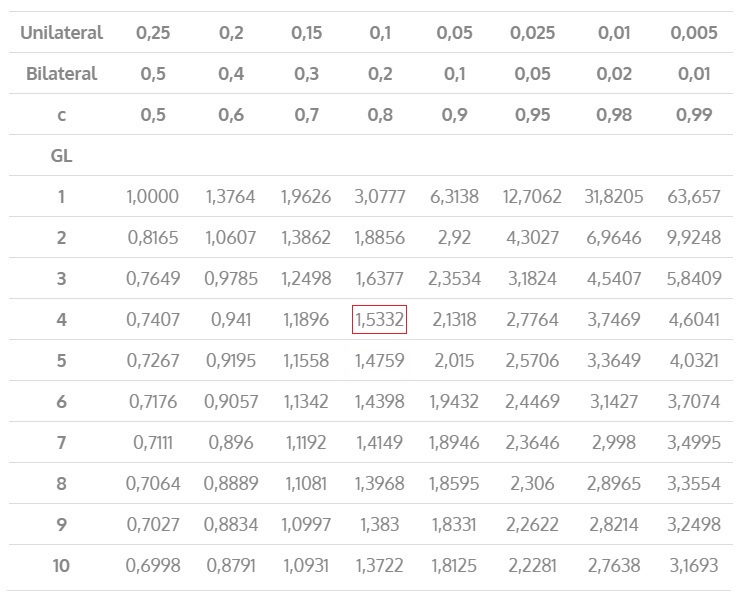
Para o cálculo dos limites de confiança, segundo a Teoria Estatística das Pequenas Amostras (n<30), temos:
\mathrm{x_{máx}=\overline{x}+t_{(c;n-1)}\cdot\left[\dfrac{S}{\sqrt{(n-1)}}\right]=374,31+1,5332\cdot\left[\dfrac{66,00}{\sqrt{4}}\right]}
xmáx= R$ 494,91 /m²
\mathrm{x_{mín}=\overline{x}-t_{(c;n-1)}\cdot\left[\dfrac{S}{\sqrt{(n-1)}}\right]=374,31-1,5332\cdot\left[\dfrac{66,00}{\sqrt{4}}\right]}
xmín= R$ 323,72 /m²
Tabela 15 – Valor percentual para a distribuição “t” de para grau de liberdade n-1 e grau de confiança “c”
Passo 07: Cálculo do campo de arbítrio
O campo de arbítrio é outro tipo de intervalo, que engloba uma variação de mais ou menos 15% em torno do preço estimado, logo:
xmáx= R$ 430,4 /m²
xmín= R$ 318,17 /m²
No entanto, esse intervalo só é usado para arbitrar o valor do avaliando caso haja extrapolação do modelo, o que não é nosso caso.
Passo 08: Estimativa do valor do imóvel avaliando
Após o saneamento da amostra, iremos estimar o valor do imóvel avaliando, que deverá ser a soma do valor do terreno e o valor da edificação.
Valor do terreno
O valor do terreno por meio do tratamento por fatores será calculado conforme expressão a seguir:
\mathrm{V_t=\dfrac{V_u}{[1+(F_l-1)+(F_t-1)+(F_p-1)]}\cdot{A_t}}
\mathrm{V_t=\dfrac{374,31}{[1+(1-1)+(1-1)+(1-1)]}\cdot{250}}
Vt = R$ 93.578,46
Valor da construção
O valor da benfeitoria existente neste terreno pode ser calculada por:
\mathrm{V_c=A_c.CUB.P_{pa}.F_{oc}}
\mathrm{V_c=200.1431,53.0,919.0,66}
Vt = R$ 173.656,04
Valor total
Portanto, o valor final será:
VT=93.578,46+173.656,04 = R$ 267.234,50
VT = R$ 267.000,00
Passo 09: Enquadramento do modelo
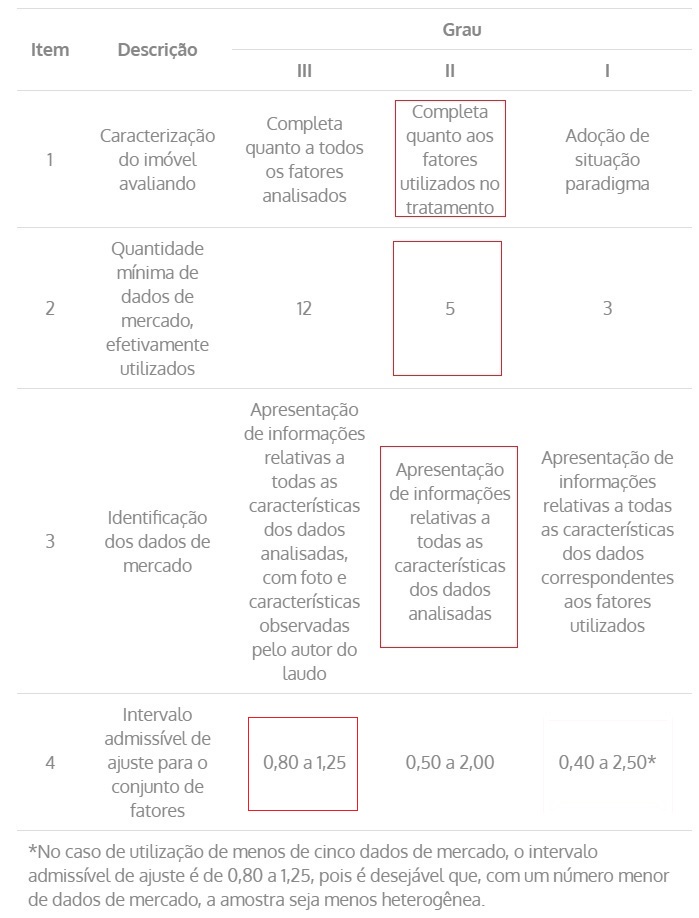
Por fim, a última etapa do tratamento por fatores é o enquadramento do modelo de acordo com o Grau de Precisão e o Grau de Fundamentação.
Primeiramente, utilizaremos a tabela 15 e classificaremos cada um dos itens no grau adequado, lembrando que o Grau III vale 3 pontos, o II vale 2 pontos e o I vale 1 ponto.
Tabela 16 – Grau de fundamentação para tratamento por fatores
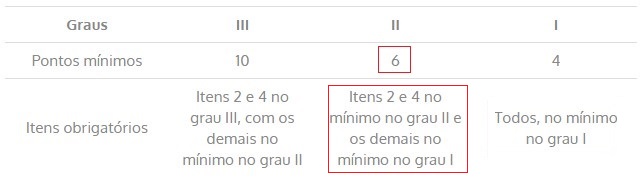
Feito isso, o resultado da pontuação foi de 09 pontos. Dessa forma, o laudo se enquadra no Grau de Fundamentação II, conforme tabela a seguir.
Tabela 17 – Critérios de enquadramento do laudo no Grau de Fundamentação
Por último, basta enquadrar o laudo (considerando a não extrapolação dos dados) na tabela 17, referente ao Grau de Precisão do modelo. Sendo a Amplitude calculada por:
\mathrm{A=\dfrac{(\overline{x}-x_{mín})+(x_{máx}-\overline{x})\cdot100}{\overline{x}}}
\mathrm{A=\dfrac{(374,31-323,72)+(460,59-374,31)}{374,31}\cdot{100}=27,03\:{\%}}
Tabela 18 – Critério de enquadramento do laudo no Grau de Precisão
RESULTADO
De posse de todos os cálculos realizados e dos dados disponíveis, o valor de mercado para a residência avaliada foi de R$ 267.234,50, podendo ser arredondado (em até 1% para mais ou menos) para o valor de R$ 267.000,00, resultando em uma Avaliação de Grau de Fundamentação II e Grau de Precisão III.
.
Pois bem, avaliadores, esse foi um breve exemplo hipotético de como dever ser feita uma avaliação de imóveis urbanos na prática, por meio do Tratamento por Fatores. E para te ajudar ainda mais preparamos um e-Book gratuito sobre Avaliação de Imóveis.
[ebook-avaliacao-imoveis]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação de Peritos Judiciais em Avaliação de Imóveis de um dos nosso parceiros, o professor Fernando Sarian, que tem mais de 17 anos de experiência na área.
Nesse curso, você irá conhecer as norma vigentes, aprenderá sobre o Avaliação Imobiliária e, o melhor de tudo, aprenderá a elaborar seu próprio laudo técnico de avaliação. Tudo isso dando um enfoque especial na área pericial e nas legislações de interesse.
Ficou curioso? É só clicar aqui.
Dito isso, ficamos por aqui e se gostou você gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
E se ainda ficou com alguma dúvida, deixe aqui nos comentários. Até o próximo post!
Fonte:
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-1:Avaliação de bens – Parte 1: Procedimentos gerais. Rio de Janeiro, 2019. 31 p.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-2:Avaliação de bens – Parte 2: Imóveis urbanos. Rio de Janeiro, 2011. 62 p.
- Ministério do Planejamento, Desenvolvimento e Gestão. Secretaria do Patrimônio da União. Manual de Avaliação.Brasília: SPU, 2017.
- COTRIM, Valéria. Avaliação básica de imóveis urbanos.Teresina: IPOG, 2019.
- INSTITUTO BRASILEIRO DE AVALIAÇÕES E PERÍCIAS DE ENGENHARIA DE SÃO PAULO. Norma para Avaliação de Imóveis Urbanos. São Paulo: IBAPE, 2011.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.