Resolvendo exercícios: viscosidade de fluidos!

Nesse post resolveremos exercícios de mecânica dos fluidos referentes a viscosidade!

Eu sei que você já leu nosso post sobre a teoria de viscosidade e já está pronto para me acompanhar na resolução dos exercícios.

Vale ressaltar também que os exercícios que serão resolvidos nesse post são exercícios do livro Mecânica dos Fluidos, de Franco Brunetti, que recomendo fortemente a leitura.

Agora, sem mais delongas, vamos começar!

Exercício 1

São dadas 2 placas planas paralelas à distância de 2 mm. A placa superior move-se com velocidade de 4 m/s, enquanto a inferior é fixa. Se o espaço entre as duas placas for preenchido com óleo (\mathrm{\nu=0,1cm^2/s} e \mathrm{\rho=830kg/m^3}), qual será a tensão de cisalhamento que atuará no óleo?

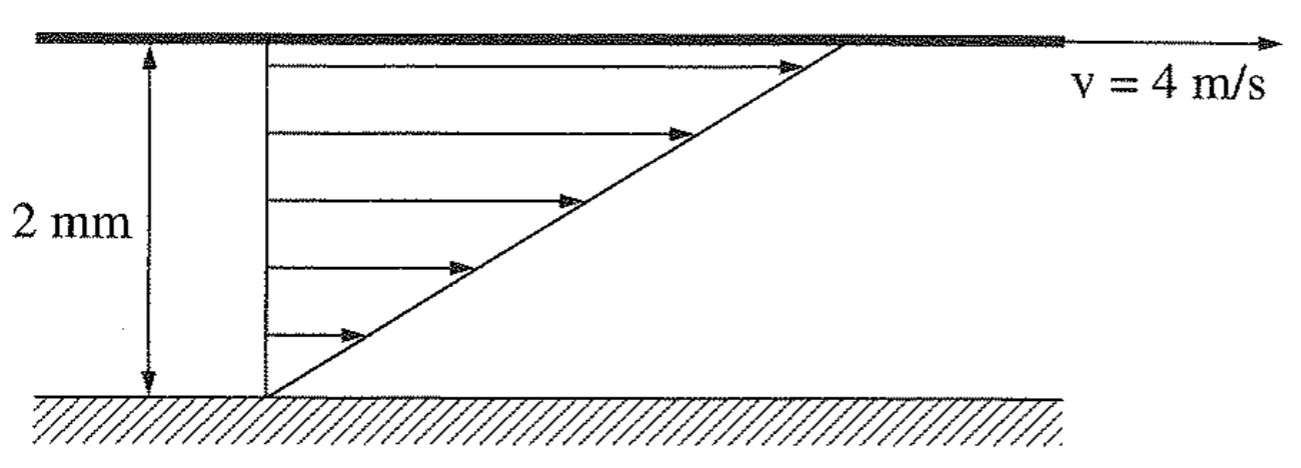
Resolução

Então, trata-se de uma questão bem simples.

Entretanto, é necessário ter conhecimento do conceito de viscosidade cinemática (\mathrm{\nu}).

Basicamente você precisa saber que:

\mathrm{\nu=\dfrac{\mu}{\rho}}

Onde:

• \mathrm{\mu}: viscosidade dinâmica do fluido;
• \mathrm{\rho}: massa específica do fluido.

Portanto, podemos calcular a viscosidade dinâmica a partir da viscosidade cinemática!

Temos, então:

\mathrm{0,1 cm^2/s=\dfrac{\mu}{830kg/m^3}}

Transformando em unidades do SI:

\mathrm{0,1\cdot 10^{-4} m^2/s=\dfrac{\mu}{830kg/m^3}}

\mathrm{\mu=8,3\cdot 10^{-3}N.s/m^2}

Agora que já determinamos o valor da viscosidade dinâmica, podemos aplicar a lei de Newton da viscosidade.

Como a espessura da camada do óleo é de apenas 2 mm e o próprio esquema da questão já nos mostra uma distribuição de velocidade linear, podemos utilizar a simplificação da lei de Newton.

\mathrm{\tau=\mu\cdot\dfrac{v_o}{\varepsilon}}

Então, agora é só uma aplicação direta da fórmula!

\mathrm{\tau=8,3\cdot 10^{-3}\dfrac{4}{2\cdot 10^{-3}}}

\mathrm{\tau=16,6 N/m^2}

Viu como não é tão complicado!

Agora vamos resolver o segundo exercício!

Exercício 2

Uma placa quadrada de 1,0m de lado e 20N de peso desliza sobre um plano inclinado de 30º, sobre uma película de óleo. A velocidade da placa é de 2 m/s constante. Qual a viscosidade dinâmica do óleo, se a espessura da película é de 2 mm?

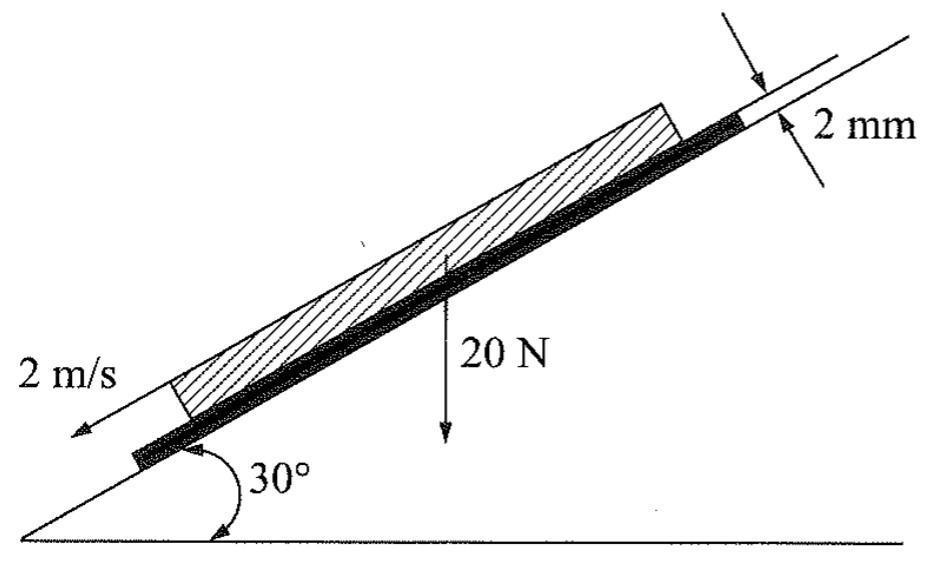
Resolução

Então, essa é uma questão clássica de plano inclinado envolvendo viscosidade de fluidos.

É importante que você preste atenção no enunciado!

Ele afirma que a placa move-se em velocidade constante.

E o que isso quer dizer?

Que a placa está em equilíbrio dinâmico! Ou seja, o somatório de forças que agem sobre a placa é igual a zero!

Logo, vamos analisar as forças que atuam sobre a placa.

Perceba que decompomos o peso da placa (P) em uma parcela normal (Pn) e outra parcela tangente (Pt).

Além disso, chamei de Fvis a força relativa a tensão de cisalhamento ocasionada pela viscosidade do óleo.

Então, como as forças a placa está em equilíbrio, podemos afirmar que:

\mathrm{F_{vis}=P_T}

\mathrm{P_N=N}

Como estamos interessados na tensão de cisalhamento causada pela viscosidade, vamos analisar a primeira igualdade.

Vamos então, inicialmente, determinar o valor de \mathrm{P_T}.

Essa tarefa é bem simples, basta uma simples análise para perceber que:

\mathrm{P_T=P \cdot sen30º}

\mathrm{P_T=20 \cdot sen30º}

\mathrm{P_T=10N}

Pronto! Agora basta calcularmos a tensão de cisalhamento para determinarmos a viscosidade dinâmica do fluido.

Então, pelo próprio conceito de tensão, temos que:

\mathrm{\tau=\dfrac{F_{vis}}{A}}

Onde A representa a área de aplicação de Fvis.

Como a placa é quadrada de lado 1,0m, temos que a área de atuação vale 1,0 m².

Além disso, lembre que \mathrm{F_vis=P_T}. Logo:

\mathrm{\tau= 10 N/m^2}

Então, agora basta aplicarmos a lei de Newton da viscosidade simplificada:

\mathrm{\tau=\mu\cdot\dfrac{v_o}{\varepsilon}}

\mathrm{10=\mu\cdot\dfrac{2}{2\cdot 10^{-3}}}

\mathrm{\mu=10^{-2}N.s/m^2}

Pronto! Já resolvemos juntos duas questões e tenho certeza que você está acompanhando tudo.

Assim, vamos agora para a terceira questão!

Exercício 3

A placa da figura abaixo tem uma área de 4,0 m² e espessura desprezível. Entre a placa e o solo existe um fluido que escoa, formando um diagrama de velocidades dado por:

\mathrm{v=20y\cdot v_{max}\cdot (1-5y)}

A viscosidade dinâmica do fluido é de \mathrm{10^{-2} N.s/m^2} e a velocidade máxima de escoamento é de 4 m/s. Pede-se:

a) O gradiente de velocidades junto ao solo.

b) A força necessária para manter a placa em equilíbrio.

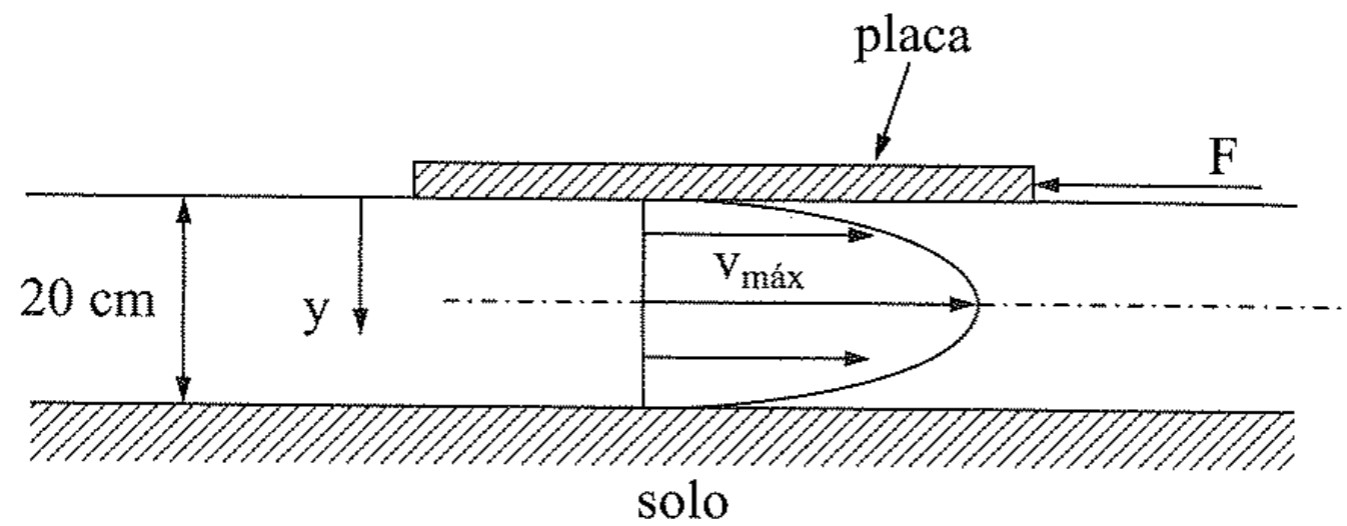
Resolução item a)

Então, vamos iniciar pelo item a)

Essa questão, diferentemente das duas anteriores, não se trata de uma simplificação da Lei de Newton da viscosidade.

Então, teremos que utilizar a seguinte formulação:

\mathrm{\tau=\mu\cdot\dfrac{dv}{dy}}

Entretanto, o item a) apenas pede o gradiente de velocidades no solo.

E o que vem a ser o gradiente de velocidades?

Simples:

\mathrm{\dfrac{dv}{dy}}

Então, inicialmente vamos determinar a formulação da velocidade, depois teremos que derivar a mesma em y.

Assim, como sabemos que a velocidade máxima é 4m/s, temos:

\mathrm{v=20y\cdot v_{max}\cdot (1-5y)}

\mathrm{v=80y - 400y^2}

Então, podemos dizer que o gradiente de velocidades é:

\mathrm{\dfrac{dv}{dy}=80 - 800y}

Pela figura, percebemos que o eixo das ordenadas tem sentido “para baixo” com origem na placa.

Então, como queremos o gradiente de velocidade no solo, temos que y=0,2m:

\mathrm{\dfrac{dv}{dy}=80 - 800y}

\mathrm{\dfrac{dv}{dy}=80 - 800\cdot0,2}

\mathrm{\dfrac{dv}{dy}=-80 s^{-1}}

Já determinamos o gradiente de velocidades no solo.

Então, agora vamos para o item b).

Resolução item b)

Nesse item, precisamos calcular a força para manter a placa em equilíbrio.

Ou seja, basta calcularmos a força ocasionada pela viscosidade do fluido!

Entretanto, diferentemente do item a), agora precisamos calcular o gradiente de velocidades para a placa.

Então, como o eixo tem início da placa, podemos afirmar que para a placa, y=0. Logo:

\mathrm{\dfrac{dv}{dy}=80 - 800y}

\mathrm{\dfrac{dv}{dy}=80 s^{-1}}

Agora, vamos utilizar a lei de Newton de viscosidade:

\mathrm{\tau=\mu\cdot dfrac{dv}{dy}}

\mathrm{\tau=10^{-2}\cdot 80}

\mathrm{\tau=0,8 N/m^2}

Por fim, aplicando o conceito básico de tensão, temos:

\mathrm{\tau=\dfrac{F}{A}}

Como a área da placa é de 4,0m², temos:

\mathrm{0,8=\dfrac{F}{4}}

\mathrm{F=3,2N}

Pronto! Para equilibrar a placa, temos que aplicar na mesma uma força de 3,2N em sentido contrário a força causada pela viscosidade do fluido!

Considerações finais

Então, nesse post nós exercitamos toda a teoria aprendida sobre viscosidade dos fluidos e lei de Newton da viscosidade.

Espero que você tenha aprendido tudo, entretanto, se você ainda ficou com alguma dúvida, pode deixar nos comentários que vai ser um prazer te responder!

Além disso, continue seguindo nosso blog e nos acompanhando no YouTube.

Por fim, até a próxima! =)

---

Fonte: BRUNETTI, F. Mecânica dos Fluidos. Ed. Pearson Prentice Hall. São Paulo. 2a Ed. 2008;