Muitas vezes a arquitetura requer que utilizemos uma viga em balanço em nosso projeto estrutural, não é?
A boa notícia é que nessa publicação você irá encontrar tudo que precisa para calcular a área de aço necessária para essa viga.
No final você ainda vai encontrar um exemplo prático em que dimensionaremos uma viga em balanço.
Análise de uma viga em balanço
Primeiramente, devemos partir para obtenção dos esforços na viga em balanço. Para isso, em primeiro lugar, devemos verificar o que fornece o engastamento do balanço. O mesmo pode ser dado por uma continuidade da própria viga ou um engastamento fornecido pelo pilar.
Eu recomendo que você opte pela continuidade, uma vez que o engastamento diretamente no pilar requer um nível maior de atenção na da rigidez do pilar.
Observe a seguir um modelo de viga em balanço com carga distribuída:
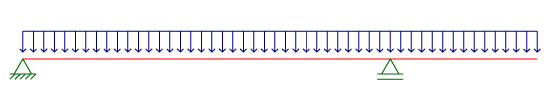
Nesse caso, temos o vão interno bem superior ao vão em balanço. Dessa forma, teremos um momento positivo considerável:

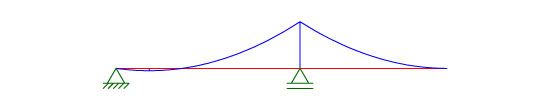
Em situações em que a dimensão do tramo interno é próxima da dimensão do tramo externo, praticamente não teremos momentos positivos no trecho interno, conforme ilustra o resultado abaixo:
Cálculo da armadura
A fim de realizar o dimensionamento de área de aço de uma viga em balanço, vamos basicamente utilizar os mesmo conceitos já empregados no cálculo da área de aço de flexão simples.
A única diferença que teremos, para o dimensionamento da armadura, é que como se trata de um trecho em balanço, a área principal estará posicionada na região superior da viga.
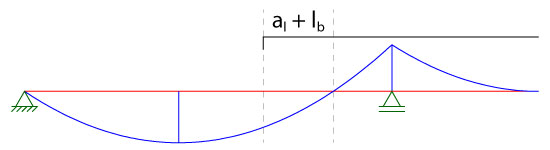
Para o detalhamento da armação longitudinal ao longo da viga, basta analisarmos tanto a decalagem do diagrama momento fletor quanto a ancoragem dessas barras, conforme ilustra a figura abaixo:
Exemplo de viga em balanço
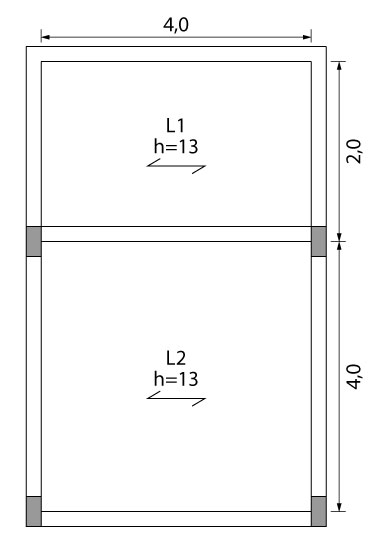
Com o intuito de aplicarmos o conteúdo estudado, vamos calcular a área de aço de um viga em balanço que apoia uma laje nervurada. Na situação ilustrada abaixo vemos duas lajes treliçadas de 13 cm de altura apoiadas sobre vigas de concreto armado.
Caso você prefira, também pode acompanhar toda essa resolução através do vídeo abaixo:
Em toda estrutura apresentada acima foi considerado um concreto classe C25, ou seja, com resistência característica de 25 MPa.
Além do carregamento oriundo da laje, temos alvenaria de 3,0 m de altura na região interna e 1,0 m de altura na região externa.
O objetivo desse exemplo é encontrarmos a área de aço necessária na região de máximo momento negativo.
Pré-dimensionamento
Antes de mais nada, vamos supor algumas dimensões para as vigas que recebem a laje nervurada. Nós podemos pré-dimensionar a altura de vigas com 10% do vão no caso do primeiro trecho e 5% para o trecho livre.
Assim sendo, assumiremos todas as vigas com 40 cm de altura. Para a largura, vamos considerar 20 cm.
Levantamento dos carregamentos
A fim de facilitar o entendimento, vamos chamar a viga que possui o trecho em balanço de viga lateral e a viga na extremidade da varanda de viga externa.
Carregamento decorrente da laje nervurada
Em primeiro lugar, nós temos que obter os carregamentos oriundos das lajes aplicados na viga lateral. Para isso, vamos considerar nervuras distribuídas a cada 45 cm, vide figura abaixo:
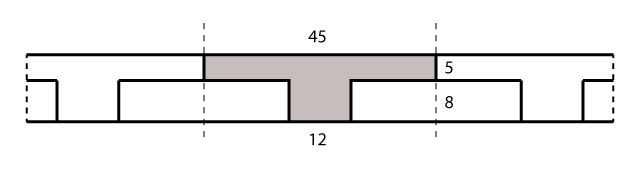
A partir da publicação sobre laje nervurada, temos um carregamento de 2,63 kN/m em cada nervura. Esse carregamento já leva em consideração o peso do concreto, o enchimento, o revestimento e a sobrecarga de utilização atuante na laje.
Uma vez que essas nervuras tem um vão de 4,0 m e que metade da carga irá para cada viga, temos:
\mathrm{\dfrac{2,63 \cdot 4}{2} = 5,26 \; kN}
Logo, cada nervura aplica uma ação de 5,26 kN em cada uma das vigas. Visto que, temos uma nervura a cada 45 cm, o carregamento distribuído por metro na viga lateral será:
\mathrm{\dfrac{5,26}{0,45} = 11,7 \; kN/m}
Carregamento da viga externa
A ação atuante na viga externa será decorrente do peso próprio e da alvenaria de 1,0 m de altura. O peso próprio pode ser calculado pelo produto da área transversal e do peso específico do concreto:
\mathrm{p_{concreto} = 0,2 \cdot 0,4 \cdot 25 = 2 \; kN/m}
Nós podemos obter o peso da alvenaria a partir da Tabela 5.2 da ABNT/NBR: 6120 (2019). Ao considerarmos uma alvenaria de bloco cerâmico vazado de 14 cm de espessura, com revestimento de 1,0 cm em cada lado, teremos 1,4 kN/m². Assim sendo, para um altura de 1,0 m de alvenaria o carregamento será 1,4 kN/m.

Visto que essa viga é apoiada nas duas vigas laterais, e que temos um total de 3,4 kN/m (2 + 1,4), teremos na extremidade de cada viga lateral uma carga pontual de:
\mathrm{\dfrac{3,4 \cdot 4,2}{2}= 7,14 \; kN}
Peso próprio e alvenaria na viga lateral
Além do carregamento oriundo da laje e da viga externa, ainda teremos o peso próprio e a alvenaria sobre a viga lateral.
Para o trecho externo da viga lateral, teremos o mesmo valor encontrado para viga externa, ou seja, 3,4 kN/m.
Já no trecho interno, a diferença está na altura da alvenaria, que gera um carregamento de 4,2 kN/m. Totalizando assim 6,2 kN/m (4,2 + 2,0).
Esforços
Com o intuito de obtermos o momento fletor para a viga lateral, vamos utilizar o software Ftool para lançar a estrutura em questão. A mesma possui dois vãos, o primeiro com 4,0 m e o segundo com 2,0 m.
No modelo, teremos basicamente o carregamento distribuído para o trecho interno:
\mathrm{p_{laje} + p_{concreto} + p_{alvenaria}}
\mathrm{11,7 + 2,0 + 4,2 = 17,9 \; kN/m}
E teremos também o trecho externo:
\mathrm{p_{laje} + p_{concreto} + p_{alvenaria}}
\mathrm{11,7 + 2,0 + 1,4 = 15,1 \; kN/m}
Por fim, chegamos ao modelo no Ftool. Observe na figura abaixo que também incluímos a carga pontual de 7,1 kN decorrente da viga externa.
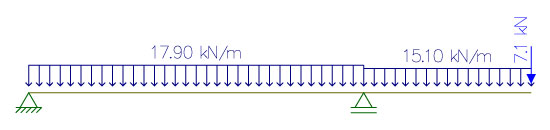
Podemos analisar agora o diagrama momento fletor (DMF) gerado pelo software:

Dimensionamento da área de aço
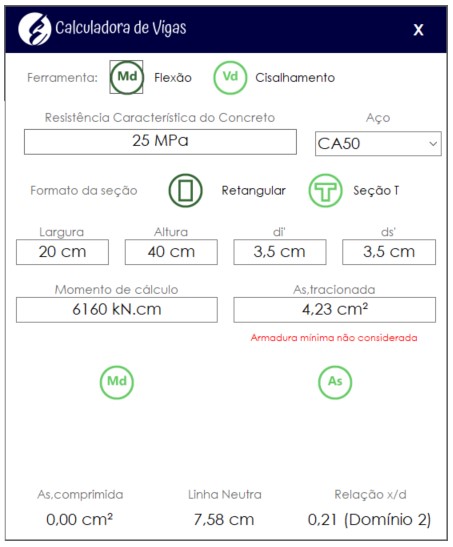
O dimensionamento da armação do trecho em balanço será dado em função do momento de 44 kN.m. Para isso, vamos utilizar as mesmas formulações já conhecidas de seções submetidas à flexão simples.
Primeiramente, vamos calcular o valor de k, utilizado no cálculo da profundidade da linha neutra:
\mathrm{k=\dfrac{M_{Sd}}{b_w \cdot f_{cd}} }
\mathrm{k = \dfrac{1,4 \cdot 4400}{20 \cdot \dfrac{2,5}{1,4}} = 172,5 \; cm^2}
Em seguida, vamos para a obtenção da linha neutra em si. Irei considerar aqui a altura útil de 36,5 cm.
\mathrm{\dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
\mathrm{\dfrac{24,8 \pm \sqrt{0,4624 \cdot 1.332 - 187,7}}{0,544}}
\mathrm { x = \left\{ \begin{array}{ll} 83,67 \; cm \\ 7,58 \; cm \end{array} \right. }
Uma vez que o exemplo se trata de uma viga submetida à flexão simples (sem presença de esforços normais), não seria possível uma linha neutra que não cortasse a seção. Assim sendo, podemos desconsiderar o resultado de \mathrm{x = 83,67} \; cm.
Cálculo da área de aço
Em posse agora da profundidade da linha neutra, é possível determinar o valor do braço de alavanca:
\mathrm{z = d - 0,4 \cdot x}
\mathrm{z = 36,5 - 0,4 \cdot 7,58 = 33,5 \; cm}
Em seguida, podemos calcular a área de aço necessária:
\mathrm{A_s =\dfrac{M_{Sd}}{z \cdot f_{yd}}}
\mathrm{A_s =\dfrac{1,4 \cdot 4400}{33,5 \cdot 43,5} = 4,23 \; cm^2}
Também seria possível ter obtido a área de aço dessa viga utilizando nossa Calculadora de Vigas gratuita:
Seleção da armação para viga em balanço
Com o propósito de selecionarmos a armação a ser utilizada na região superior de nossa viga, vamos utilizar a tabela abaixo, que traz a área de aço ao combinarmos bitola com quantidade.
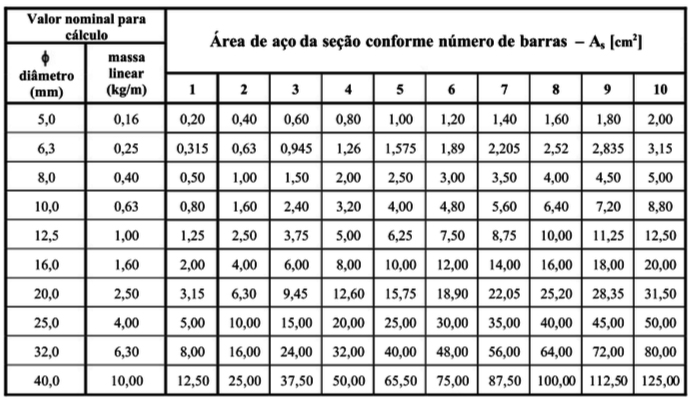
Por fim, como necessitamos de 4,23 cm², podemos utilizar 4 barras de 12,5 mm, o que nos fornece uma área efetiva de 5,00 cm².
Recado final
No final desse vídeo você já deve saber analisar uma viga em balanço. Mas lembre-se a obtenção da área de aço longitudinal é apenas uma das etapas de um projeto estrutural.
Além disso, teremos outras verificações, como por exemplo: deslocamentos, cisalhamento e o próprio detalhamento da seção transversal.
Peço que também nos ajude compartilhando esse conteúdo com aquele seu amigo ou amiga que curte estruturas.
Forte abraço!
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Que show! Obrigado pelo conteúdo!
Bom. Um prazer escrever para vc Engenheiro.
Assisto os seus vídeos sobre as estruturas isso me ajudou bastantes em compreender muitos conteúdos.
Ianique Abna-Guiné-Bissau
Feliz que tenha lhe ajudado!
Um grande abraço!
parabéns, sempre vejo sua publicações
Valeu, Paulo!