Projetos rodoviários: curva vertical

Todo mundo gosta de uma estrada plana, não é mesmo? Você consegue viajar bem mais rápido, não perde seu precioso tempo tentando ultrapassar os caminhões e nem arrisca sua segurança.

Seria ótimo se todas as estradas fossem perfeitamente retas e planas, mas a realidade é bem diferente. Isso porque há varias limitações para isso, como os obstáculos da natureza ou os altos de custo de regularização do terreno.

É aí que as rampas e as curvas verticias entram para facilitar a construção das estradas e garantir a sua continuidade quando, por exemplo, o terreno de base da estrada é extremamente montanhoso ou, até mesmo, para evitar custos excessivos durante a sua execução.

É por isso mesmo que, nesse post, estudaremos as curvas verticias do tipo simples e ainda aprenderemos como calcular as cotas das estacas pertencentes a ela.

Mas antes de começarmos nossa aventura aqui, recomendamos que dê uma rápida olhada no nosso post anterior sobre projeto longitudinal rodoviário e seus elementos, clicando aqui.

Agora vamos lá?

Tipos de curvas verticais

Conforme vimos no último post, as curvas verticais tem o principal objetivo de realizar a concordância entre duas rampas e podem ser de dois tipos: côncavas ou convexas, conforme veremos na imagem a seguir.

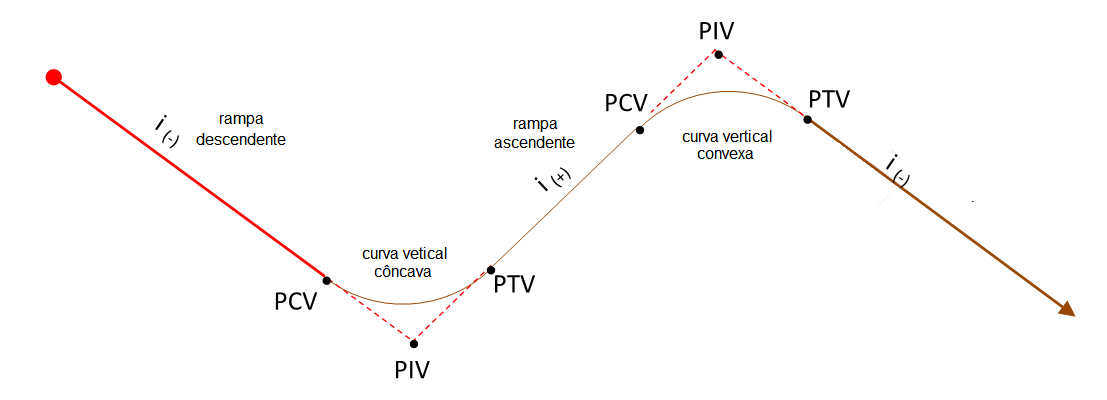
Para realizar essa concordância, podemos utilizar diversos tipos de curvatura, como, por exemplo, circunferências, elipses ou parábolas de 2º ou 3º grau.

No entanto, a curvatura do tipo parábola do 2º grau é a mais utiliza por apresentar uma taxa de variação da declividade constante e pela facilidade de cálculo das cotas.

É por essa razão que é o tipo de curvatura recomendada pelo Departamento Nacional de Infraestrutura e Transportes (DNIT) e é o tipo que estudaremos aqui e agora.

Principais elementos da curva vertical

Para começarmos a entender o projeto de curvatura de uma estrada, iremos agora conhecer os elementos componentes da curva horizontal simples.

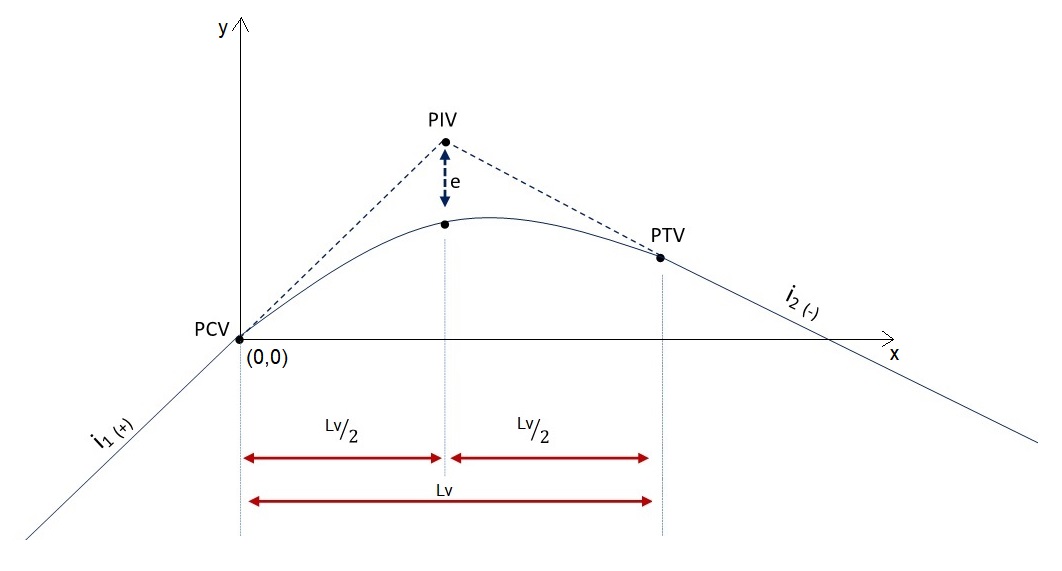
Ponto de interseção das tangentes (PIV)

O ponto de interseção, como o próprio nome sugere, é o ponto de encontro entre as duas tangentes à parábola, ou seja, entre o prolongamento de duas rampas consecutivas.

Ponto de curva vertical (PCV)

Este ponto caracteriza-se por ser o ponto de transição entre a primeira rampa e a curva vertical.

Ponto de tangente vertical (PTV)

O PTV, por sua vez, é o ponto de transição entre a curva vertical e a segunda rampa.

Comprimento da curva vertical (Lv)

Lv é a o comprimento projetado, ou seja, na horizontal, de curva vertical e pode ser medido pela diferença entre as estacas PTV e PCV.

Flecha (e)

A flecha é a diferença de cotas entre dois pontos de mesma abscissa situados na tangente e na curva vertical.

Esse elemento é extremamente importante para a que a regularização do terreno onde a estrada deverá ser assentada, ou seja, é através dele que conseguimos obter o perfil longitudinal adequado para a estrada.

Como calcular a curva vertical

Conforme já foi dito, a cura vertical que trataremos aqui será a parabólica do segundo grau, que tanto pode ser simples como composta. Neste post, veremos como calcular uma curva vertical simples, que é aquele em que os pontos PCV e PTV então equidistantes em relação a PIV.

1. Calcular o comprimento mínimo da curva

De início, precisamos determinar o comprimento ideal para a curva vertical. Para isso, iremos aprender a obter o comprimento mínimo permitido levando em conta a distância de visibilidade adequada para que o condutor tenha condições de realizar uma frenagem segura.

Dessa forma, antes de tudo, a distância de visibilidade (S) não pode ser inferior à distância de frenagem (Df).

Agora, iremos estudar 2 casos diferentes para ambos os tipos de curvas, sempre considerando a situação mais desfavorável, em que S = Df.

Vale lembrar que ambos os casos apresentados dever ser calculados, sendo o comprimento mínimo o maior dentre os dois, considerando sempre o mínimo absoluto, que é igual a 0,6.V_p.  

Curvas convexas

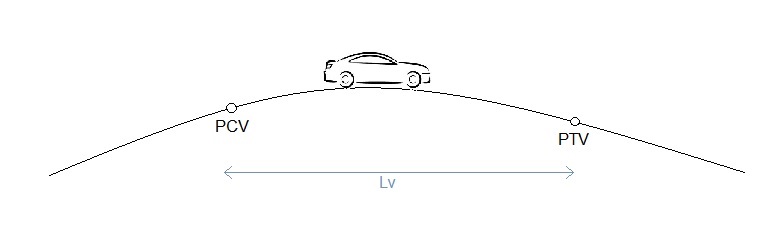
1º caso: S = Df ≤ Lv

Nesse primeiro caso, a distância de visibilidade é menor ou igual ao comprimento da curva, o que significa que, na situação mais desfavorável, tanto o veículo quando um obstáculo estão sobre a curva.

Desse modo, o comprimento mínimo é calculado pela expressão a seguir:

\mathrm{Lv_{mín}=\dfrac{|i_2-i_1|.Df^2}{4,04}}

Onde:

• Lv_mín é o comprimento mínimo da curva vertical (m), Lv_mín ≥ 0,6.V_p;
• V_p é a velocidade diretriz de projeto (km/h);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal);
• Df é a distância de frenagem (m).

2º caso: S = Df ≥ Lv

Para o segundo caso, a distância de visibilidade é maior ou igual ao comprimento da curva. Desse modo, o comprimento mínimo é calculado por:

\mathrm{Lv_{mín}=2.Df-\dfrac{4,04}{|i_2-i_1|}}

Onde:

• Lv_mín é o comprimento mínimo da curva vertical (m), Lv_mín ≥ 0,6.V_p;
• V_p é a velocidade diretriz de projeto (km/h);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal);
• Df é a distância de frenagem (m).

Curvas côncavas

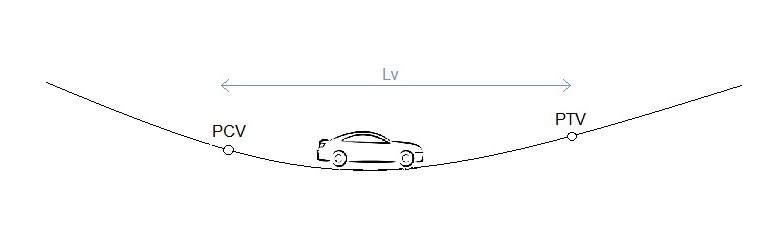
1º caso: S = Df ≤ Lv

\mathrm{Lv_{mín}=\dfrac{|i_2-i_1|.Df^2}{1,2+0,035.Df}}

Onde:

• Lv_mín é o comprimento mínimo da curva vertical (m), Lv_mín ≥ 0,6.V_p;
• V_p é a velocidade diretriz de projeto (km/h);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal);
• Df é a distância de frenagem (m).

2º caso: S = Df ≥ Lv

\mathrm{Lv_{mín}=2.Df-\dfrac{1,+0,035.Df}{|i_2-i_1|}}

Onde:

• Lv_mín é o comprimento mínimo da curva vertical (m), Lv_mín ≥ 0,6.V_p;
• V_p é a velocidade diretriz de projeto (km/h);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal);
• Df é a distância de frenagem (m).

2. Encontrar a equação da parábola  

Agora que já sabemos qual é o comprimento adequado para a curva vertical, é imprescindível que conheçamos sua equação y=ax²+bx+c. Para isso, basta que situemos o PCV na origem do eixo cartesiano e utilizemos as informações já conhecidas como, por exemplo, a inclinação das rampas que também são as tangentes da parábola.

Pois bem, sabemos que, como que a parábola cruza o eixo y na origem, c=0. Além disso, como a tangente ou devida no PCV (x=0) é igual à inclinação da primeira rampa i₁, temos:

\mathrm{\dfrac{dy}{dx}=i_1}

\mathrm{2ax+b=i_1}

\mathrm{b=i_1}

Da mesma forma, como a tangente no PTV (x=Lv) é igual à inclinação da segunda rampa i_2, temos:

\mathrm{\dfrac{dy}{dx}=i_2}

\mathrm{2ax+b=i_2}

\mathrm{2a(Lv)+i_1=i_2}

\mathrm{a=\dfrac{i_2-i_1}{2Lv}}

Desse modo, facilmente encontramos a equação

\mathrm{y=\dfrac{i_2-i_1}{2Lv}\cdot{x^2}+i_1.x}

Onde:

• y é a cota de um ponto em relação à estaca PCV (m);
• x é a distância de um ponto em relação à estaca PCV (m);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal);
• Lv é o comprimento da curva vertical (m).

Conhecendo a equação, conseguimos agora determinar a cota de qualquer ponto da curva somando o valor de y no ponto à cota do PCV.

Outra forma de também calcularmos as cotas é por meio da flecha em relação à primeira tangente e, assim, a cota de qualquer ponto na curva será a cota na tangente menos a flecha nesse ponto.

[ebook-projetos-rodoviarios]

3. Calcular a equação da flecha

Cabemos que a flecha é a diferença de conta entre a tangente e a parábola, dessa forma, temos:

\mathrm{e=i_1.x-\dfrac{i_2-i_1}{2Lv}\cdot{x^2}+i_1.x}

\mathrm{e=\dfrac{i_1-i_2}{2Lv}\cdot{x^2}}

Se preferir, a equação da flecha também pode ser dada em função da flecha máxima, ao invés de utilizar as inclinações das rampas, vejamos.

Sabemos que a flecha máxima ocorre no PIV (x=Lv/2), então:

\mathrm{e_{máx}=\dfrac{i_1-i_2}{2Lv}\cdot{(Lv/2)^2}}

\mathrm{e_{máx}=\dfrac{i_1-i_2}{2Lv}\cdot{Lv^2/4}}

\mathrm{e_{máx}=\dfrac{Lv.(i_1-i_2)}{8}}

Onde:

• e_máx é a flecha máxima da curva (m);
• Lv é o comprimento da curva vertical (m);
• i₁ é a inclinação da primeira rampa (decimal);
• i₂ é a inclinação da segunda rampa (decimal).

Agora, isolaremos i_1-i_2 para substituirmos na equação da flecha:

\mathrm{i_1-i_2=\dfrac{8.e_{máx}}{Lv}}

\mathrm{e=\dfrac{(8.e_{máx}/Lv)}{2Lv}\cdot{x^2}}

\mathrm{e_1=\dfrac{4.e_{máx}}{Lv^2}\cdot{x^2}}

Onde:

• e₁ é a flecha em um ponto situado no primeiro ramo da curva (m);
• e_máx é a flecha máxima da curva (m);
• Lv é o comprimento da curva vertical (m);
• x é a distância de um ponto em relação à estaca PCV (m).

Para a equação da flecha acima, é importante nos atentarmos que ela somente é válida para o primeiro ramo, ou seja, para x ≤ Lv/2, para o segundo ramo, utilizaremos a equação abaixo:

\mathrm{e_2=\dfrac{4.e_{máx}}{Lv^2}\cdot{(Lv-x)^2}}

Onde:

• e₂ é a flecha em um ponto situado no segundo ramo da curva (m);
• e_máx é a flecha máxima da curva (m);
• Lv é o comprimento da curva vertical (m);
• x é a distância de um ponto em relação à estaca PCV (m).

4. Calcular as cotas

Por fim, o último passo será calcular as cotas das estadas pertencentes à curva vertical.

Pontos notáveis PCT e PTV

\mathrm{Cota_{\:PCV}=Cota_{\:PIV}-\dfrac{Lv.i_1}{2}}

\mathrm{Cota_{\:PTV}=Cota_{\:PIV}+\dfrac{Lv.i_2}{2}}

Ponto qualquer em relação a PIV

Para calcularmos a cota em qualquer ponto da curva vertical utilizaremos a equação da flecha em relação à cota do PIV, considerando os dois ramos da curva, separadamente, conforme abaixo:

1º ramo (antes do PIV)

\mathrm{Cota_{\:P}=Cota_{\:PIV}-d.i_1-\dfrac{4.e_{máx}}{Lv^2}\cdot{d^2}}

2º ramo (depois do PIV)

\mathrm{Cota_{\:P}=Cota_{\:PIV}+d.i_2-\dfrac{4.e_{máx}}{Lv^2}\cdot{(Lv/2-d)^2}}

.

Pois bem pessoal, essas foram algumas considerações a respeito das curvas verticais e não esquecer de clicar aqui para conferir o exercício resolvido sobre esse mesmo assunto para que não restem mais dúvidas!

Ou, se preferir, confira o e-Book gratuito sobre Projeto Rodoviário que preparamos pra você.

[ebook-projetos-rodoviarios]

É claro, no entanto, que esse universo é muuuuito mais amplo do que conseguimos abordar em um e-Book.

Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.

Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades..

---

Fonte:

ALBUQUERQUE, Marcos. Projeto vertical. Teresina: UFPI, 2017.

MACEDO, Edivaldo Lins. Noções de Topografia Para Projetos Rodoviarios.  2008. Disponível em: <http://www.topografiageral.com/>. Acesso em: 26 agosto 2019.

.