No nosso post anterior sobre Curvas Verticias, explicamos o que é e como devemos calcular alguns dos principais seus elementos.
Portanto, se você ainda não leu esse post, recomendamos que dê uma rápida olhada antes de começarmos.
Agora, vamos solidificar o que foi aprendido sobre Perfil Longitudinal até o momento. Para tanto, propomos um exemplo prático bem simples.
Confira abaixo!
Exemplo prático
Você é responsável por um projeto rodoviário e necessita encontrar as cotas referentes a uma curva de concordância vertical, sabendo que:
- O estaqueamento da estrada é feito a cada 20 m;
- A distância de visibilidade de frenagem é 75 m;
- A velocidade diretriz da estrada 80 km/h;
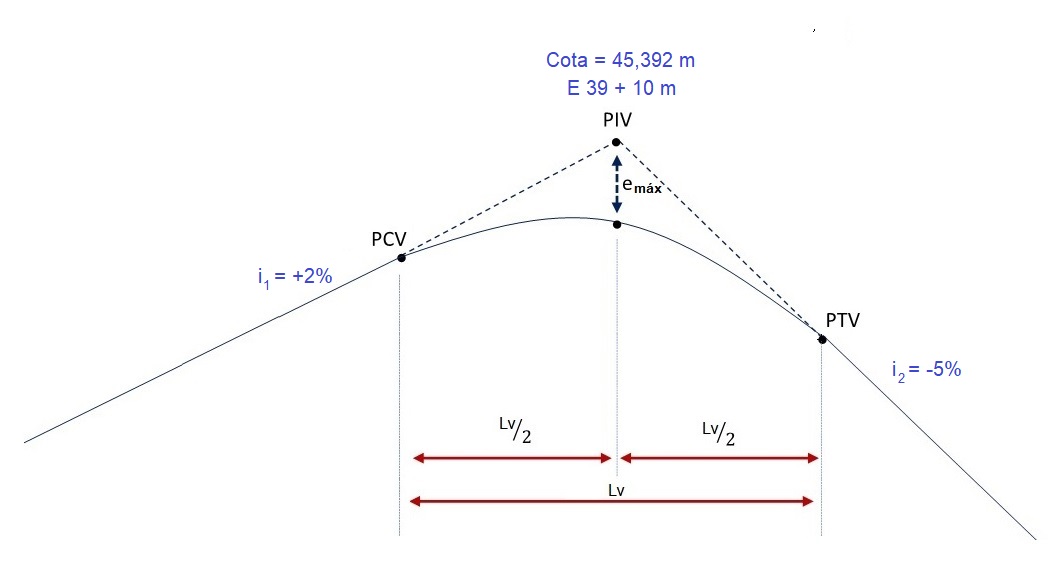
- O ponto de interseção vertical dessa curva está localizado na estaca 39 + 10 m, onde a cota é 45,392 m.
RESOLUÇÃO:
Passo 01: Calcular o comprimento da curva
O primeiro passo para resolvermos esse exemplo é determinar o comprimento necessário para a curva vertical.
Para isso, iremos obter o comprimento mínimo permitido levando em conta a distância de visibilidade adequada para que o condutor tenha condições de realizar uma frenagem segura, de acordo com os critérios a seguir.
Comprimento mínimo absoluto
\mathrm{Lv_{mín}=0,6.V_p}
\mathrm{Lv_{mín}=0,6.80=48\:m}
1º caso: S = Df ≤ Lv
Nesse primeiro caso, a distância de frenagem é menor ou igual ao comprimento da curva e é calculado pela expressão a seguir:
\mathrm{Lv_{mín}=\dfrac{|i_2-i_1|.Df^2}{4,04}}
\mathrm{Lv_{mín}=\dfrac{|-0,05-0,02|.110^2}{4,04}=97,46\:m}
2º caso: S = Df ≥ Lv
Para o segundo caso, a distância de visibilidade é maior ou igual ao comprimento da curva. Desse modo, o comprimento mínimo é calculado por:
\mathrm{Lv_{mín}=2.Df-\dfrac{4,04}{|i_2-i_1|}}
\mathrm{Lv_{mín}=2.110-\dfrac{4,04}{|-0,05-0,02|}=95,29\:m}
Podemos perceber que o caso 1 oferece o maior comprimento mínimo dentre os dois casos, sendo ambos superiores ao valor mínimo absoluto. Desse modo, iremos adotar para o comprimento da curva o valor do caso 1 arredondado, logo:
Lv = 100 m
2. Localizar os pontos PCV e PTV na curva
Para calcular a cota das estacas da curva precisamos antes situá-las no eixo da estrada. Dessa forma, sabendo que o ponto PIV está localizado na estaca 39 + 10 m, temos:
\mathrm{E_{PCV}=E_{PIV}-Lv/2}
\mathrm{E_{PCV}=E\:39+10\:m-100/2=E\:39-40\:m}
\mathrm{E_{PCV}=E\:37}
\mathrm{E_{PTV}=E_{PCV}+Lv}
\mathrm{E_{PTV}=E\:37+100\:m}
\mathrm{E_{PTV}=E\:42}
3. Calcular a flecha máxima
Agora, calcularemos a flecha máxima da curva vertical para que possamos utilizar esse valor na equação geral da flecha.
\mathrm{e_{máx}=\dfrac{Lv.(i_1-i_2)}{8}}
\mathrm{e_{máx}=\dfrac{100.[0,02-(-0,05)]}{8}}
\mathrm{e_{máx}=0,875\:m} [ebook-projetos-rodoviarios]
4. Calcular as cotas
Por fim, o último passo será calcular a cota das estadas pertencentes à curva vertical e, para isso, utilizaremos a equação apresentada abaixo, lembrando que a equação é diferente no primeiro e no segundo ramo da curva.
E 37 (PCV) – 1º ramo
\mathrm{Cota_{\:P}=Cota_{\:PIV}-d.i_1-\dfrac{4.e_{máx}}{Lv^2}\cdot{(Lv/2-d)^2}}
\mathrm{Cota_{\:PCV}=45,392-50.0,02-\dfrac{4.0,875}{100^2}\cdot{(100/2-50)^2}}
\mathrm{Cota_{\:PCV}=44,392\:m}
E 38 – 1º ramo
\mathrm{Cota_{\:E38}=45,392-30.0,02-\dfrac{4.0,875}{100^2}\cdot{(50-30)^2}}
\mathrm{Cota_{\:E38}=44,652\:m}
E 39 – 1º ramo
\mathrm{Cota_{\:E39}=45,392-10.0,02-\dfrac{4.0,875}{100^2}\cdot{(50-10)^2}}
\mathrm{Cota_{\:E39}=44,632\:m}
E 40 – 2º ramo
\mathrm{Cota_{\:P}=Cota_{\:PIV}+d.i_2-\dfrac{4.e_{máx}}{Lv^2}\cdot{(Lv/2-d)^2}}
\mathrm{Cota_{E40}=45,392+10.(-0,05)-\dfrac{4.0,875}{100^2}\cdot{(100/2-10)^2}}
\mathrm{Cota_{\:E40}=44,332\:m}
E 41 – 2º ramo
\mathrm{Cota_{E41}=45,392+30.(-0,05)-\dfrac{4.0,875}{100^2}\cdot{(100/2-30)^2}}
\mathrm{Cota_{\:E41}=43,752\:m}
E 42 (PTV) – 2º ramo
\mathrm{Cota_{\:PTV}=45,392+50.(-0,05)-\dfrac{4.(0,875)}{100^2}\cdot{(100/2-50)^2}}
\mathrm{Cota_{\:PTV}=42,892\:m}
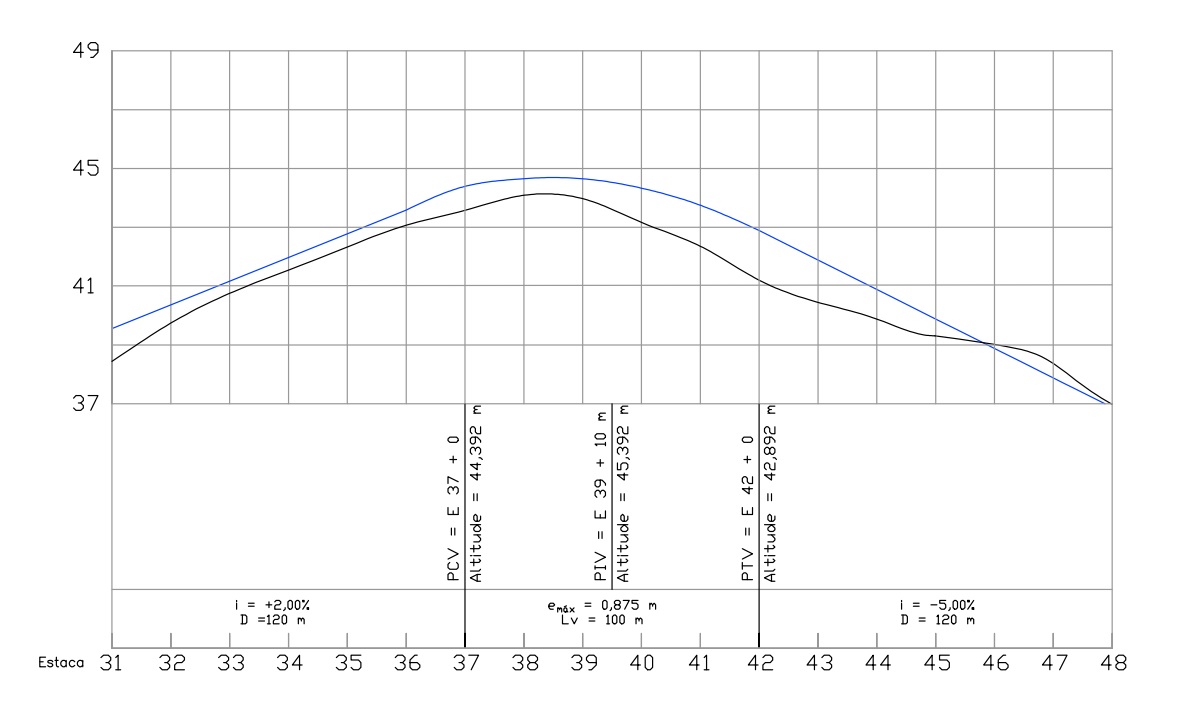
Resultado final
O resultado final do estaqueamento da curva vertical do nosso exemplo está apresentado a seguir, onde o greide do projeto, composto por rampas ascendentes e descendentes e uma curva vertical convexa, está representado em azul.
.
Pois bem pessoal, essas foram algumas considerações a respeito das curvas verticais, espero muito que esse post tenha sido útil pra você.
Ah, e não deixe de conferir o super e-Book gratuito sobre Projeto Rodoviário que preparamos pra você!!!
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muuuito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar de verdade nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades..
Fonte:
ALBUQUERQUE, Marcos. Projeto vertical. Teresina: UFPI, 2017.
PIMENTA, Carlos R. T. et al. Projeto Geométrico de Rodovias. 2. ed. São Carlos: RiMA, 2004.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.