Dimensionamento simples para peças de madeira

Olá, engenheiros! Nesse post, você aprenderá como dimensionar peças maciças de madeira por meio dos critérios de segurança da ABNT NBR 7190/97 e ainda preparamos um ótimo exemplo de como calcular as dimensões de uma tesoura de madeira.

Se quiser conferir como se calcula a resistência de uma estrutura de madeira, veja nosso post anterior.

Boa leitura!

Critérios de segurança no estado limite último

Abaixo, os critérios de segurança exigidos para uma estrutura de madeira em diversas situações.

Compressão paralela às fibras

Em peças de madeira submetidas à compressão axial, o critério de segurança é dado por:

\mathrm{σ_{cd}≤f_{cd}}

Onde:

• σ_cd: é a tensão solicitante de projeto na compressão longitudinal às fibras (kN/m²);
• f_cd: é a tensão resitente de projeto na compressão longitudinal às fibras (kN/m²).

Flambagem

A compressão axial pode provocar flambagem na peça, diminuindo sua estabilidade. Isso depende tanto da esbeltez da peça quanto da magnitude da força axial aplicada.

Limite de esbeltez

Para peças comprimidas, segundo a NBR 7190/97, o limite de esbeltez de uma peça deverá ser menor ou igual a 140 para que haja estabilidade. A esbeltez é, então, calculada por:

\mathrm{λ=\dfrac{L_{fl}}{i}}

Onde:

• λ: é o coeficiente de esbeltez da peça;
• Lfl: é o comprimento de flambagem (m);
• i: é o raio de giração da seção transversal (m).

Para colunas curtas

0< Lfl/i≤40

Para colunas medianamente esbeltas

40< Lfl/i≤80

Para colunas esbeltas

80< Lfl/i≤140

Comprimento de flambagem

O comprimento de famblagem é o valor teórico considerado para o cálculo da flambagem e leva em consideração as condições de contorno da estrutura.

 

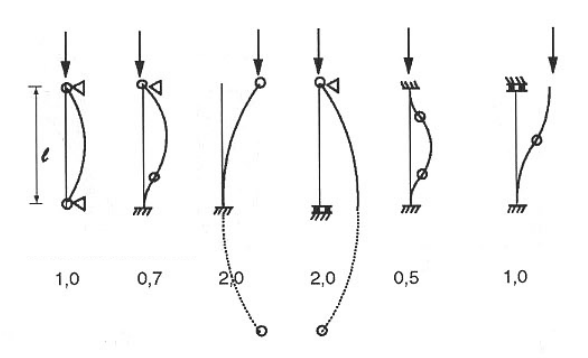
\mathrm{L_{fl}=K.L}

Onde:

• K: é o parâmetro de flambagem, esquema acima;
• L é o comprimento real da peça (m).

Compressão normal às fibras

Já em peças de madeira submetidas à compressão normal às fibras, o critério de segurança é dado por:

\mathrm{σ_{cnd}<f_{cnd}}

\mathrm{f_{cnd}=0,25.f_{cd}.σ _n}

Onde:

• σ_cnd: é a tensão solicitante de projeto na compressão normal às fibras (kN/m²);
• f_cnd: é a tensão resistente de projeto na compressão normal às fibras (kN/m²);
• σ_n: é um coeficiente que leva em conta a maior rigidez da madeira para esforço aplicados em pequena área, tabela 1.

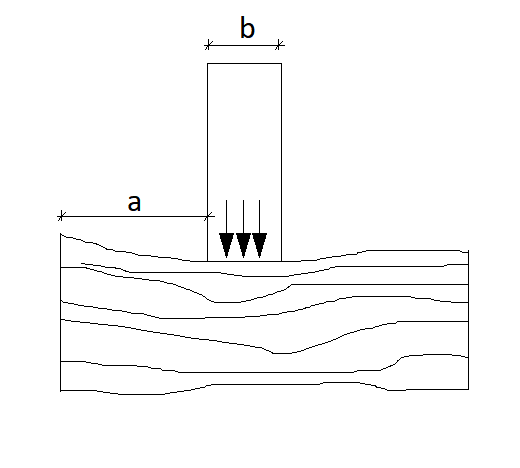
Tabela 1 – Coeficiente σ_n de acréscimo da tensão resistente de compressão normal às fibras em função de b.

Compressão inclinada em relação às fibras

Em relação à compressão longitudinal e normal, a compressão inclinada é intermediária às duas acima. Dessa forma, o critério de segurança é função do ângulo de inclinação β é dado por:

\mathrm{σ_{cβd}<f_{cβd}}

\mathrm{f_{cβd}=\dfrac{ f_{cd}. f_{cnd}}{ f_{cd}{sen}^2β+ f_{cnd}{cos}^2β}}

Onde:

• β é o ângulo de inclinação com a horizontal (graus) e β>6֯, caso contrário será considerada compressão normal;
• σ_cβd: é a tensão solicitante de projeto na compressão inclinada (kN/m²);
• f_cβd: é a tensão resistente de projeto na compressão inclinada (kN/m²).

Tração

O critério de segurança para peças sujeitas à tração paralela às fibras da madeira é dado por:

\mathrm{σ_{td}≤f_{td}}

Onde:

• σ_td: é a tensão solicitante de projeto na tração longitudinal às fibras (kN/m²);
• f_td: é a tensão resistente de projeto na tração longitudinal às fibras (kN/m²).

Flexão simples reta

Para uma peça sujeita à flexão em torno de um eixo principal de inércia, as tensões normais de bordo dever atender às seguintes condições, já conhecidas:

\mathrm{σ_{cd}≤f_{cd}}

\mathrm{σ_{td}≤f_{td}}

Sendo σ_d calculada por:

\mathrm{σ_{d}≤M_{d}/W}

Onde:

• σ_d: é a tensão solicitante de projeto na flexão simples (kN/m²);
• M_d: é o momento fletor de projeto (kN.m);
• W: é o módulo de resistência à flexão do bordo considerado (m³) e equivale à razão entre o momento de inércia e a distância da linha neutra à fibra externa.

Cisalhamento longitudinal

Em peças submetidas à flexão com esforço cortante, o critério de segurança referente às tenções cisalhantes é dado por:

\mathrm{τ_{cd}≤f_{vd}}

Onde:

• τ_cd: é a tensão solicitante de projeto no cisalhamento paralelo às fibras (kN/m²);
• f_vd: é a tensão resistente de projeto no cisalhamento paralelo às fibras (kN/m²) e vale:

Para a madeira das árvores coníferas

\mathrm{f_{vd}=0,12.f_{cd}}

Para a madeira das árvores dicotiledôneas

\mathrm{f_{vd}=0,10.f_{cd}}

Exemplo aplicado

Dimensione a treliça de madeira abaixo sujeita ao carregamento dado, considerando a madeira do tipo Maçaranduba com f_cd=1,592kN/cm² e f_td=2,068kN/cm².

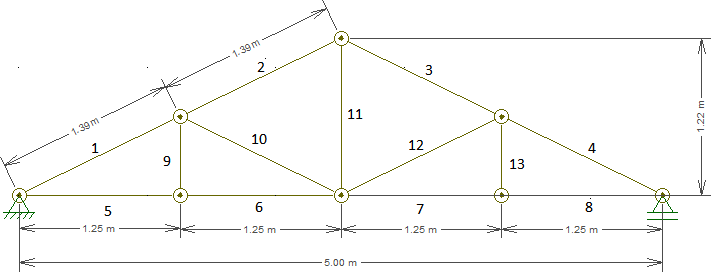
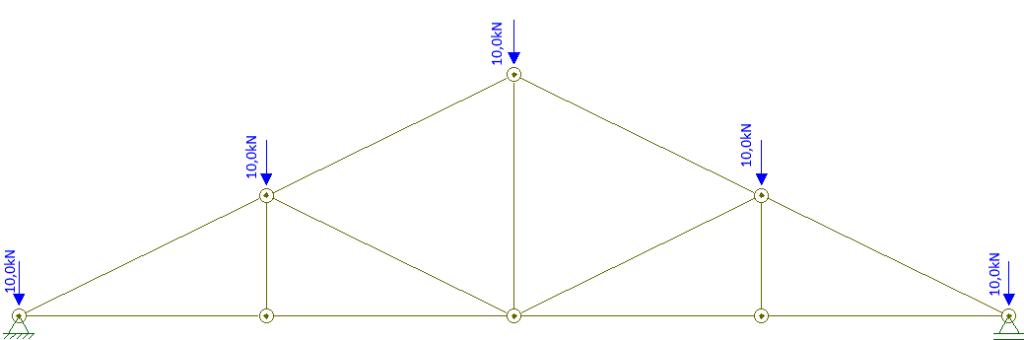
RESOLUÇÃO:

Passo 01: Esforços resultantes nas barras da treliça

Para facilitar, o cálculo dos esforços nas barras da treliça foram feitos por meio do software Ftool e está mostrado na figura abaixo.

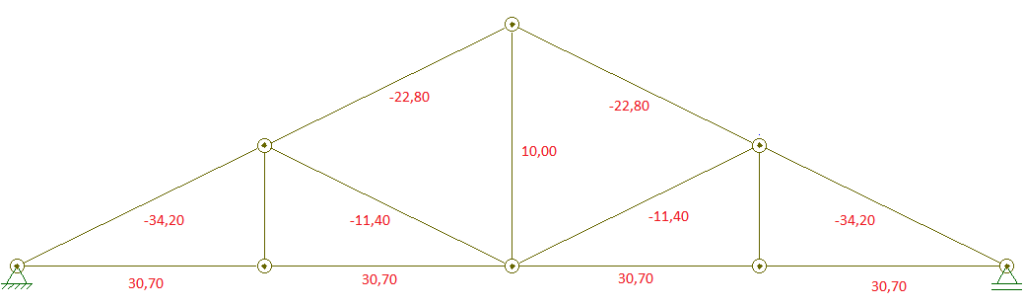
Passo 02: Dimensionamento das barras do banzo superior solicitadas à compressão

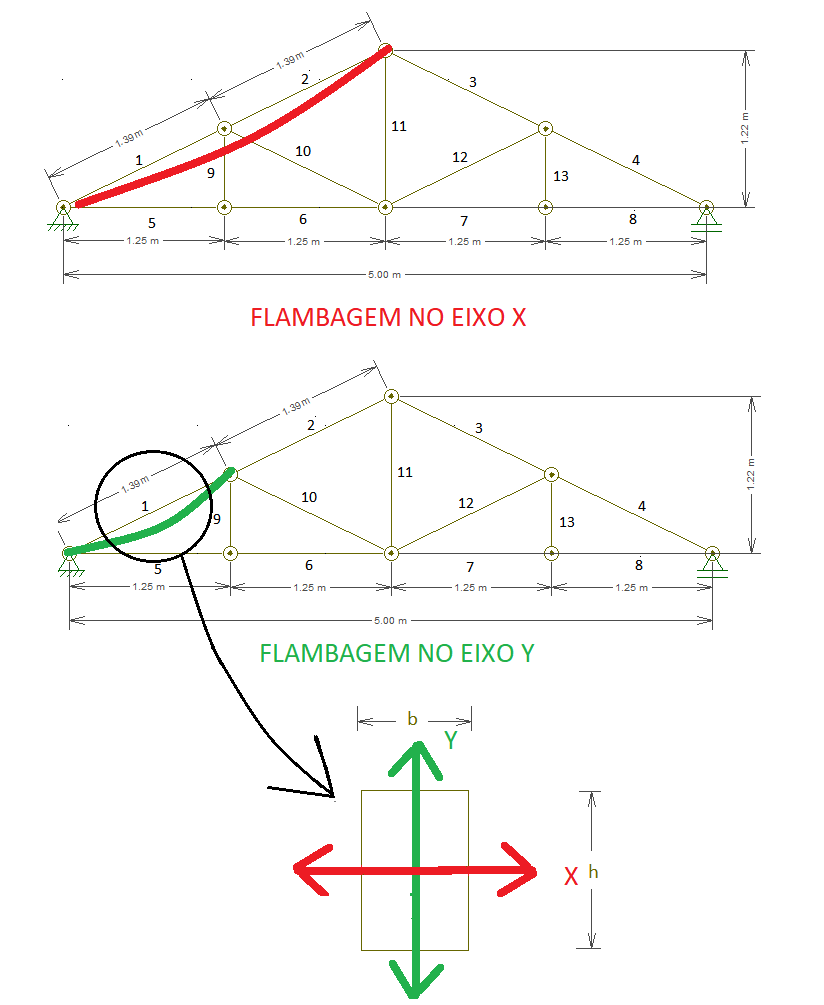
Para peças comprimidas, segundo a NBR 7190/97, a esbeltez da peça deverá ser menor que 140 para que haja estabilidade. As condições de apoio são consideradas birrotuladas e peça será dimensionada para compressão centrada, logo o comprimento de flambagem é igual ao comprimento da peça. Então:

\mathrm{λ=\dfrac{Lfl}{i}}

Onde:

• λ: é o coeficiente de esbeltez da peça;
• Lfl: é o comprimento de flambagem (m);
• i: é o raio de giração da seção transversal (m).

Para o eixo x

\mathrm{λx =Lx/ix≤140}

\mathrm{ix≥Lx/140=2,78/140=1,986cm}

\mathrm{h=ix.\sqrt{12}=6,817cm}

Para o eixo y

\mathrm{λy =Ly/iy≤140}

\mathrm{iy≥Ly/140=1,39/140=0,993cm}

\mathrm{b=iy.\sqrt{12}=3,439cm}

Logo, de acordo com o resultado acima e com a tabela 2, a seção comercial mínima adotada, inicialmente,  seria 7,0 x 7,0.

Tabela 2 – Dimensões padrão para peças de madeira serrada.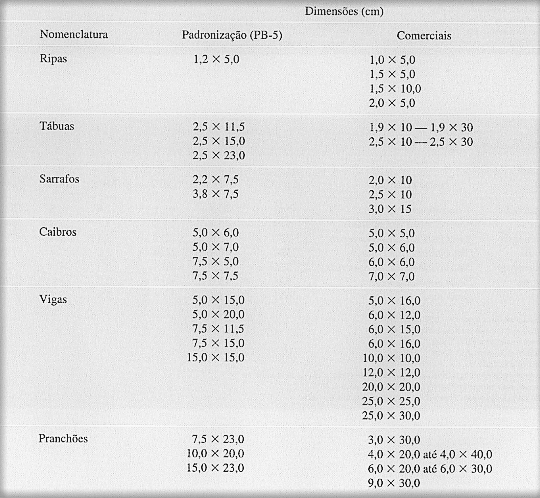

Entretanto, para elementos principais a área mínima da seção transversal adotada deverá ser maior que 50 cm² e ter espessura maior que 5 cm, segundo o item 10.2.1 da NBR 7190. Seguido esses critérios, a verificação se iniciará pela seção 6,0×12,0.

Verificação para a seção 6,0 x 12,0

A tabela 3, extraída da NBR 7190, mostra os valores médios para a madeira Maçaranduba.

Tabela 3 – Valores de resistência da madeira Maçaranduba.

Para a verificação, faremos uso das tabelas de Pfeil e Pfeil abaixo. Mas antes calcularemos os dados de entrada:

\mathrm{Ec/fc=22733/82,9=274,22}

\mathrm{λ_{crítico}=Lfl/i=139/1,45≈96} ⇒ Usaremos, neste caso, o cruzamento entre a linha 90 e a coluna 6

Coeficiente de fluência \mathrm{φ=2,0} (caso mais desfavorável)

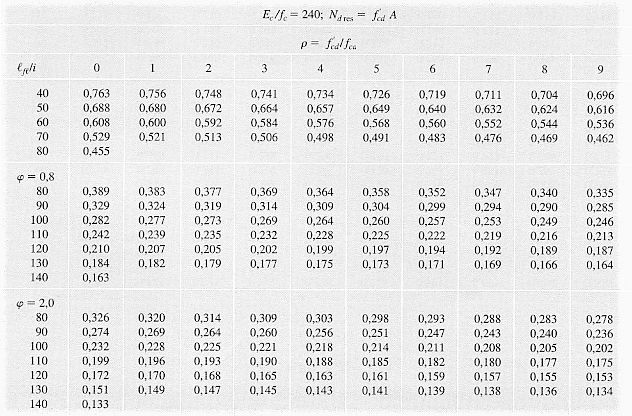
Tabela 4 – Valores de ρ para peça de madeira de seção retangular, Ec/fc=240.

 

 

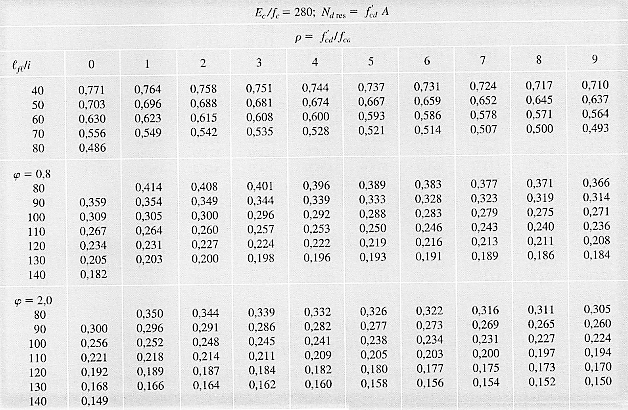
Tabela 5 – Valores de ρ para peça de madeira de seção retangular, Ec/fc=280.

Como o valor de Ec/fc está entre 240 e 280, será necessário uma interpolação entre as duas tabelas:

\mathrm{\dfrac{280-274,22}{280-240}=\dfrac{0,273-ρ}{0,273-0,247}}

\mathrm{ρ=f'_{cd}/f_{cd}=0,269}

                          \mathrm{f'_{cd}=ρ.f_{cd}=0,269.1,592=0,429kN/cm^2}

Logo,

\mathrm{σ_{cd}=\dfrac{|F_{máxima}|}{A_{existente}}=\dfrac{34,20}{6.12}=0,475kN/cm^2}

Como f’_cd<σ_cd, então a seção 6,0×12,0 não atende.

Verificação para a seção 5,0 x 16,0

\mathrm{Ec/fc=22733/82,9=274,22}

\mathrm{λ_{crítico}=Lfl/i=139/1,45≈96}

\mathrm{φ=2,0} (mais desfavorável)

Por interpolação temos:

\mathrm{\dfrac{280-274,22}{280-240}=\dfrac{0,273-ρ}{0,273-0,247}}

\mathrm{ρ=f'_{cd}/f_{cd}=0,269}

                              \mathrm{f'_{cd}=ρ.f_{cd}=0,269.1,592=0,429kN/cm^2}

Logo,

\mathrm{σ_{cd}=\dfrac{|F_{máxima}|}{A_{existente}}=\dfrac{34,20}{5.16}=0,427kN/cm^2}

Como f’_cd>σ_cd, então a seção 5,0×16,0 resiste aos esforço e será utilizada para as barras comprimidas 1, 2, 3, e 4.

Passo 03: Dimensionamento das diagonais solicitadas à compressão

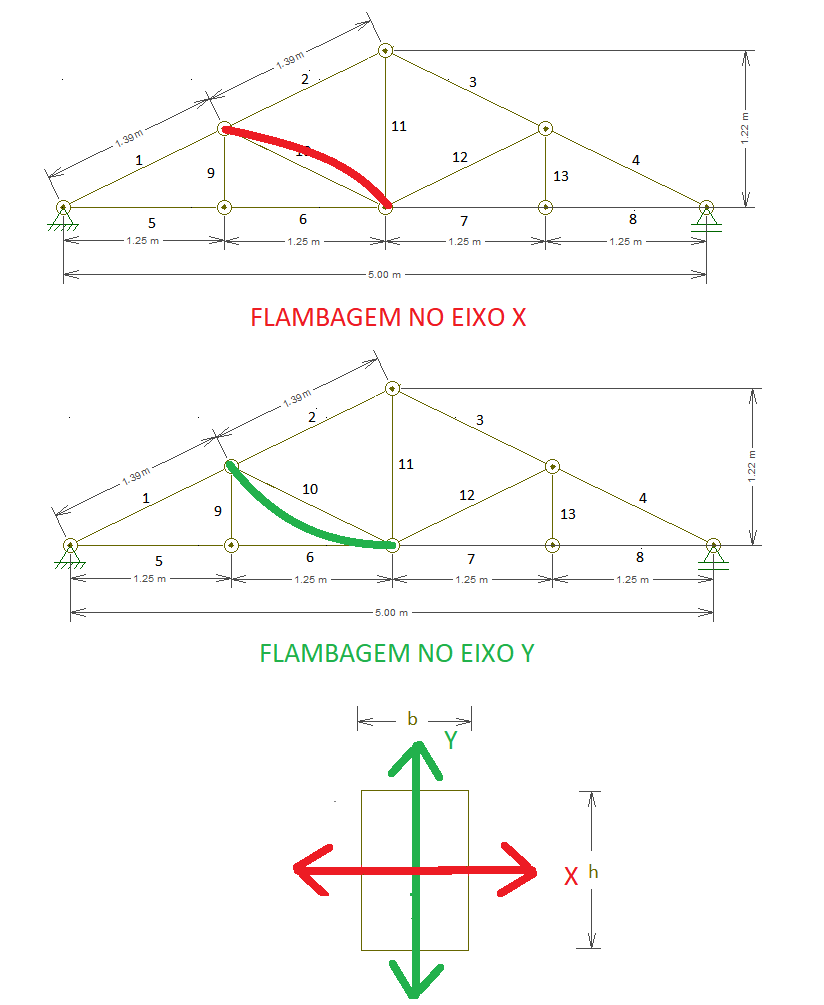
Para ambos os eixos

\mathrm{λ=Lfl/i≤140}

\mathrm{i≥Lfl/140=1,39/140=0,993cm}

\mathrm{b=i.\sqrt{12}=3,439cm}

Logo, de acordo com o resultado acima e a tabela abaixo, a seção comercial mínima adotada, inicialmente,  seria 5,0 x 5,0.

Entretanto, para elementos principais a área mínima da seção transversal adotada deverá ser maior que 50 cm² e ter espessura maior de 5 cm, segundo o item 10.2.1 da NBR 7190. Seguido esses critérios, a verificação se iniciará pela seção 5,0×16,0.

Verificação para a seção 5,0 x 16,0

\mathrm{Ec/fc=22733/82,9=274,22}

\mathrm{λ_{crítico}=Lfl/i=139/1,45≈96}

\mathrm{φ=2,0} (mais desfavorável)

Por interpolação temos:

\mathrm{\dfrac{280-274,22}{280-240}=\dfrac{0,273-ρ}{0,273-0,247}}

\mathrm{ρ=f'_{cd}/f_{cd}=0,269}

                              \mathrm{f'_{cd}=ρ.f_{cd}=0,269.1,592=0,429kN/cm^2}

Logo,

\mathrm{σ_{cd}=\dfrac{|F_{máxima}|}{A_{existente}}=\dfrac{11,40}{5.16}=0,142kN/cm^2}

Como f’_cd>σ_cd, então a seção 5,0×16,0 resiste aos esforço e será utilizada para as barras comprimidas das diagonais 10 e 12 da treliça.

Passo 04: Dimensionamento do banzo inferior solicitado à tração

Nessa situação, não é necessário verificar a flambagem, pois a barra está sob tração. Então, é estimada uma área da seção transversal que seja suficiente para resistir a esse esforço.

\mathrm{σ_{td}≤f_{td}}

\mathrm{30,70/A≤ 2,068}

\mathrm{A≥ 14,845cm^2}

Logo, será utilizado a área mínima de 50 cm², sendo adotado o perfil comercial de 6,0 x 12,0 cm, por ser o mais econômico dentre as opções.

Passo 05: Dimensionamento da barra vertical solicitada à tração

Para a barra 11, inicialmente é estimada uma área da seção transversal que seja suficiente para resistir ao esforço de tração.

\mathrm{σ_{td}≤f_{td}}

\mathrm{10/A≤ 2,068}

\mathrm{A≥4,836cm^2}

Logo, será utilizado a área mínima de 50 cm², sendo adotado para a barra 11 o perfil comercial de 6,0 x 12,0 cm, por ser o mais econômico dentre as opções.

Passo 06: Dimensionamento das barras não solicitadas

Nas barras 9 e 13, como não estão sendo solicitadas, a seção foi apenas adotada como sendo composta de duas peças de seção 2,5×10 para que fosse possível realizar as ligações,  considerando que nas peças estruturais secundárias a área mínima é de 18 cm² e espessura mínima de 2,5 cm.

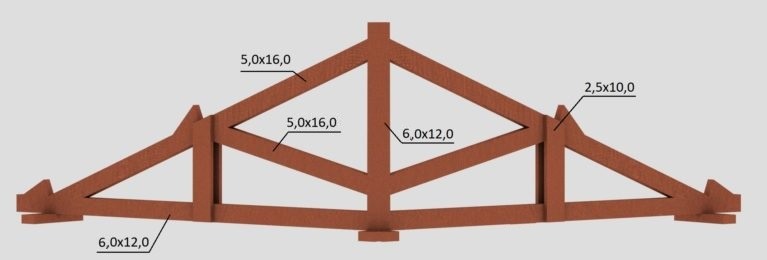
Passo 07: Resultado

As seções calculadas para as barras das treliças são apresentadas a seguir:

 

Esse post baseou-se, entre outras fontes, no livro Estruturas de Madeira de Pfeil e Pfeil, indicamos para você que tem interesse em se aprofundar mais no assunto.

Caso queira baixar o nosso e-book de Estrutura de Madeira, é só clicar aqui.

E se ainda ficou com alguma dúvida, deixe nos comentários.