Equação dos três momentos: exercícios resolvidos

Se você caiu aqui de pára-quedas, vou logo indicando que você leia inicialmente nosso post com a teoria sobre equação dos três momentos.

Mas, caso você já saiba a teoria e agora quer aprender como usar a equação dos três momentos, você está no lugar certo!

Nesse post resolveremos com você alguns exercícios de vigas contínuas através da utilização dessa equação e, prometo, que ao fim da leitura você já estará apto a utilizá-la nas mais diversas situações!

Vamos lá?

Exercício 1

Vamos iniciar com um exercício relativamente simples. Considere uma viga contínua com três apoios, conforme a figura abaixo. A viga é de concreto (considere E=25.000 MPa) e tem dimensões 15×40 cm. Sobre todo o comprimento da viga, atua sobre a mesma um carregamento linear de 1,00 kN/m. Determine o momento fletor no apoio central da viga em questão.

Resolução

Então, você já conhece a famosa equação dos três momentos:

\mathrm{\dfrac {M_{i-1} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i}}{E_{i}I_{i}}+\dfrac {M_{i+1} L_{i}}{E_{i}I_{i}}=-6\left(\dfrac{C1}{E_{i-1}I_{i-1}}+\dfrac {C2}{E_{i}I_{i}}\right)}

Sabemos que o módulo de elasticidade e o momento de inércia (relativo às dimensões da viga) são constantes e iguais em ambos os tramos, logo, podemos também cancelar tais grandezas da equação, ficando então com :

\mathrm{M_{i-1} L_{i-1}+2M_{i} L_{i-1}+2M_{i} L_{i}+M_{i+1} L_{i}=-6\left({C1}+{C2}\right)}

Sempre utilizamos a equação para o apoio que desconhecemos o momento fletor. Como a estrutura é triapoiada, sabemos que o momento fletor nos apoios extremos é igual a zero, logo utilizaremos a equação para o apoio central. Teremos então:

\mathrm{0\cdot 4+2M_{i} \cdot 4+2M_{i} \cdot 3+0\cdot 3=-6\left({C1}+{C2}\right)}

Utilizando a tabela já apresentada no post anterior, temos que:

\mathrm{{C1}=\dfrac{q\cdot L^3}{24}}

\mathrm{{C1}=\dfrac{10 kNm \cdot 4^3}{24}}

\mathbf{{C1}=26,67 kN.m^2}

\mathrm{{C2}=\dfrac{q\cdot L^3}{24}}

\mathrm{{C2}=\dfrac{10 kNm \cdot 3^3}{24}}

\mathbf{{C2}=11,25 kN.m^2}

Então, agora basta aplicarmos a equação dos três momentos:

\mathrm{0\cdot 4+2M_{i} \cdot 4+2M_{i} \cdot 3+0\cdot 3=-6\left({26,67}+{11,25}\right)}

\mathrm{14M_{i}=-227,52}

\mathbf{M_{i}=-16,25 kNm}

Pronto! Viu como é fácil a utilização da fórmula?

Agora vamos calcular as reações de apoio!

Cálculo das reações de apoio

Como vimos no post da teoria, precisamos analisar cada tramo separadamente. Então, vamos lá!

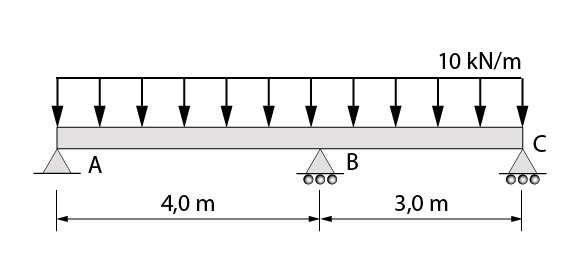
Vamos analisar inicialmente o primeiro tramo.

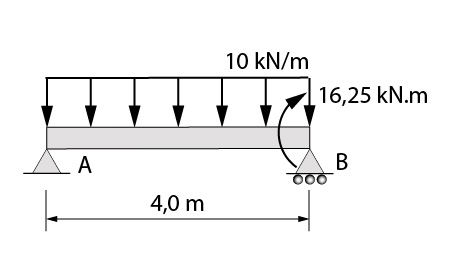
Fazendo o somatório de momentos fletores no apoio A, temos:

\mathrm{\sum M_{A}=(10 kN/m)\cdot 4m \cdot 2m + 16,25kNm - V_{B}^{e} \cdot 4m}

\mathrm{0=80 kNm + 16,25kNm - V_{B}^{e} \cdot 4m}

\mathbf{V_{B}^{e}=24,06 kN}

Logo, podemos calcular a reação no primeiro apoio pelo somatório de forças verticais.

\mathrm{\sum V=-(10 kN/m)\cdot 4m + V_{A} + V_{B}^{e}}

\mathrm{0=-(10 kN/m)\cdot 4m + V_{A} + 24,06 kN}

\mathbf{V_{A} = 15,94 kN}

Agora, vamos analisar o segundo tramo.

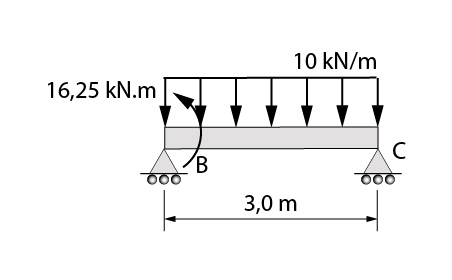
Temos que o somatório de momentos fletores para o último apoio também é igual a zero. Logo:

\mathrm{\sum M_{C}=(-10 kN/m)\cdot 3m \cdot 1,5m - 16,25kNm + V_{B}^{d} \cdot 3m}

\mathrm{0=-45 kNm - 16,25kNm + V_{B}^{d} \cdot 3m}

\mathbf{V_{B}^{d}=20,42 kN}

Por fim, podemos calcular a reação no último apoio pelo somatório de forças verticais.

\mathrm{\sum V=-(10 kN/m)\cdot 3m + V_{C} + V_{B}^{d}}

\mathrm{0=-(10 kN/m)\cdot 3m + V_{C} + 20,42 kN}

\mathbf{V_{C} = 9,58 kN}

Já descobrimos então as reações nos dois apoios extremos.

Para calcular a reação no apoio central, basta somarmos os valores obtidos para a reação nesse apoio para os dois tramos separadamente.

\mathrm{V_{B}=V_{B}^{e}+ V_{B}^{d}}

\mathrm{V_{B}=24,06kN+ 20,42kN}

\mathbf{V_{B}=44,48 kN}

Então, as reações de apoios calculadas para a viga contínua em questão são apresentadas no esquema abaixo.

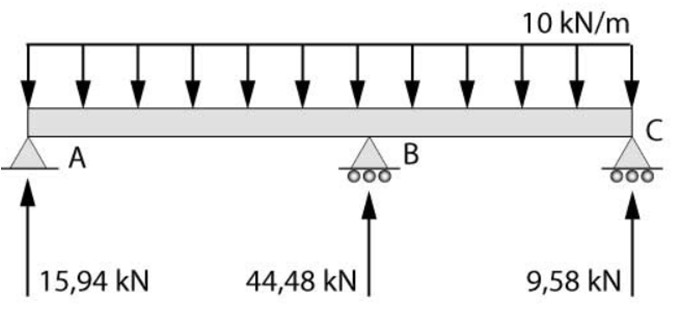
Agora vamos para um exemplo um pouco mais difícil.

Exercício 2

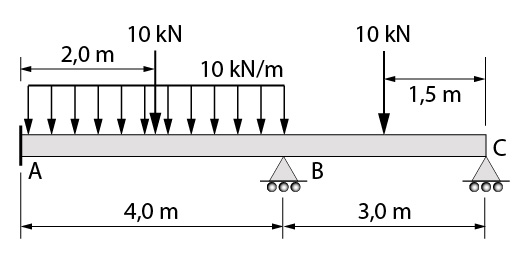
O segundo exercício é similar ao primeiro, mas iremos adicionar algumas diferenças. Inicialmente, o primeiro apoio agora será um engaste. Além disso, iremos considerar que no primeiro tramo a viga apresenta dimensões de 15×40 cm e no segundo tramo 15x30cm. O material da viga continua sendo concreto (E=25.000 MPa) e os carregamentos atuantes na mesma estão representados na figura abaixo.

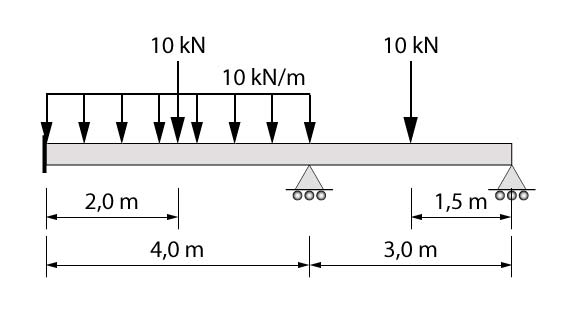
Resolução

Bem, como também já te ensinamos no nosso post sobre a teoria da equação dos três momentos, podemos substituir o engaste por uma barra de inércia infinita e comprimento diferente de zero. Logo, podemos utilizar tal modelo adaptado para simular o modelo da questão.

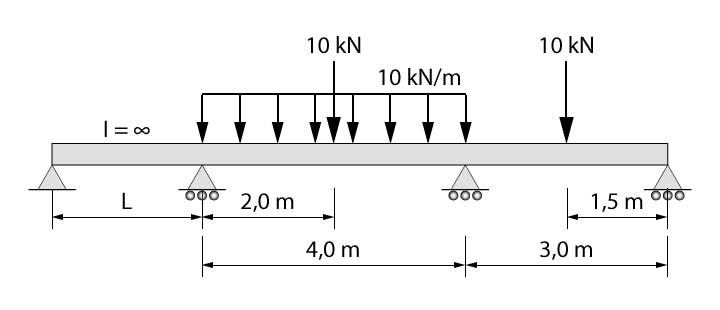
Então, sabemos que  temos 2 apoios centrais. Logo, precisaremos utilizar duas vezes a equação dos dois momentos.

Primeira utilização da equação dos três momentos

Utilizaremos inicialmente para o primeiro apoio central. Lembrando a equação:

\mathrm{\dfrac {M_{i-1} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i}}{E_{i}I_{i}}+\dfrac {M_{i+1} L_{i}}{E_{i}I_{i}}=-6\left(\dfrac{C1}{E_{i-1}I_{i-1}}+\dfrac {C2}{E_{i}I_{i}}\right)}

Analisando a figura abaixo, que representa o primeiro apoio central, temos que:

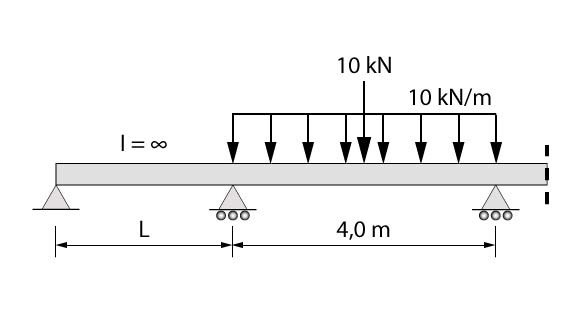
\mathrm{\dfrac {0\cdot L}{E \cdot \infty}+\dfrac {2M_{1}\cdot L}{E \cdot \infty}+\dfrac {2M_{1} \cdot 4}{25\cdot 10^9\cdot I_{1}}+\dfrac {M_{2} \cdot 4}{25\cdot 10^9 \cdot I_{1}}=-6\left(\dfrac{C1}{25\cdot 10^9\cdot \infty}+\dfrac {C2}{25\cdot 10^9\cdot I_{1}}\right)}

Lembrando que para calcular o momento de inércia de uma viga retangular, utilizamos a seguinte formulação:

\mathrm{I=\dfrac{b\cdot h^3}{12}}

Logo:

\mathrm{I_1=\dfrac{0,15m \cdot 0,40^3m^3}{12}}

\mathbf{I_1=8\cdot 10{-4}m^4}

Então, substituindo os valores de inércia na equação dos três momentos, chegamos a seguinte formulação:

\mathrm{\dfrac {2M_{1} \cdot 4}{2,0\cdot 10^7}+\dfrac {M_{2} \cdot 4}{2,0\cdot 10^7}=-6\left(\dfrac {C2}{2,0\cdot 10^7}\right)}

Basta agora só calcularmos C2. Lembrando que C2 também vai ser calculado com a tabela de C1 e C2 já apresentada no texto. Vamos fazer a superposição de um carregamento distribuído linearmente com o de uma carga pontual no meio do vão:

\mathrm{C2=\dfrac{10kN/m \cdot 4^3}{24}+\dfrac{10kN\cdot 2(4^2-2^2)}{6\cdot 4}}

\mathbf{C2=36,67 kN.m^2}

Por fim, substituindo o valor de C2 na equação já encontrada, teremos:

\mathrm{\dfrac {2M_{1} \cdot 4}{2,0\cdot 10^7}+\dfrac {M_{2} \cdot 4}{2,0\cdot 10^7}=-6\left(\dfrac {36,67\cdot 10 ^3}{2,0\cdot 10^7}\right)}

\mathrm{8M_{1}+4M_{2}=-220\cdot 10^3 N.m}

\mathbf{8M_{1}+4M_{2}=-220 kN.m}

Então, essa é a equação final para esse apoio!

Segunda utilização da equação dos três momentos

Agora, utilizaremos o mesmo fluxo de trabalho para utilizar a equação dos três momentos no segundo apoio intermediário.

A partir da análise da figura abaixo, que representa tal apoio, temos a seguinte equação dos três momentos:

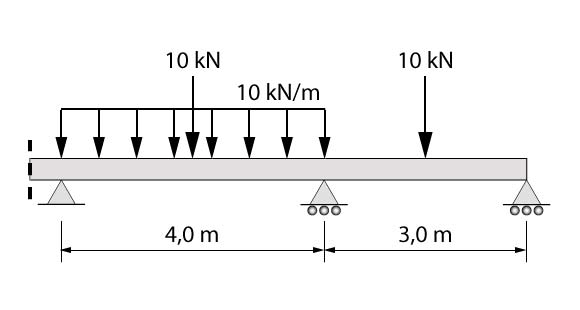
\mathrm{\dfrac {M_{1}\cdot 4}{2,0\cdot 10^7}+\dfrac {2M_{2}\cdot 4}{2,0\cdot 10^7}+\dfrac {2M_{2}\cdot 3}{25 \cdot 10^9 \cdot I_{2}}+\dfrac {0\cdot 3}{25 \cdot 10^9 \cdot I_{2}}=-6\left(\dfrac{C1}{2,0\cdot 10^7}+\dfrac {C2}{25 \cdot 10^9 \cdot I_{2}}\right)}

Então, assim como no primeiro apoio, precisamos determinar o momento de inércia do último tramo da viga, bem como os valores de C1 e C2.

Para o cálculo de I do último tramo, temos que:

\mathrm{I_2=\dfrac{0,15m \cdot 0,30^3m^3}{12}}

\mathbf{I_2=33,75\cdot 10^{-5}m^4}

Já para a determinação de C1 e C2 utilizaremos a tabela já apresentada nessa questão. Podemos perceber que o C1 para o segundo apoio é o mesmo C2 do apoio anterior, logo podemos rapidamente inferir que:

\mathbf{C1=36,67 \cdot 10^3 N.m^2}

Já para o cálculo de C2, temos:

\mathrm{C2=\dfrac{10kN\cdot 1,5(3^2-1,5^2)}{6\cdot 3}}

\mathrm{C2=5,625 kN.m^2}

\mathbf{C2=5,625 \cdot 10^3 N.m^2}

Pronto! Agora já temos a inércia da viga e os valores de C1 e C2, basta substituirmos na equação dos três momentos.

\mathrm{\dfrac {M_{1}\cdot 4}{2,0\cdot 10^7}+\dfrac {2M_{2}\cdot 4}{2,0\cdot 10^7}+\dfrac {2M_{2}\cdot 3}{84,38\cdot 10^5}=-6\left(\dfrac{36,67 \cdot 10^3}{2,0\cdot 10^7}+\dfrac {5,625 \cdot 10^3}{84,38\cdot 10^5}\right)}

\mathbf{2M_{1}+11,11M_{2}=-150\cdot 10^3 N.m}

Finalizando o cálculo dos momentos fletores

Então, nós chegamos a duas equações e temos duas incógnitas, logo podemos resolver um sistema simples de equações para determinarmos M1 e M2. Temos então:

\mathbf{8M_{1}+4M_{2}=-220 kN.m}

\mathbf{2M_{1}+11,11M_{2}=-150\cdot 10^3 N.m}

Isolando os termos, podemos chegar facilmente a seguinte solução:

\mathbf{M_{1}=-22,8 kN.m}

\mathbf{M_{2}=-9,4 kN.m}

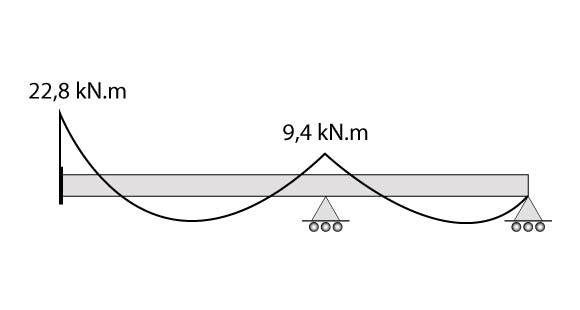
Cálculo das reações de apoio

Agora, vamos para o cálculo das reações de apoio da nossa viga.

Assim como no exemplo anterior, vamos dividir nossa viga em dois tramos, a fim de calcularmos as reações isoladamente por tramos isostáticos e em seguida, somaremos as reações do apoio intermediário para ambos tramos

Então, vamos analisar inicialmente o primeiro tramo, com os momentos fletores já calculados.

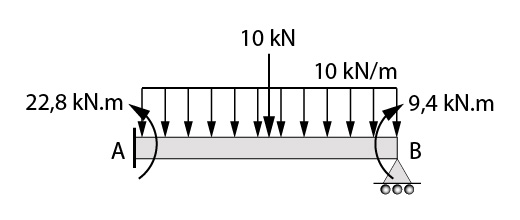
Fazendo o somatório de momentos fletores no apoio A, temos:

\mathrm{\sum M_{A}= -22,8 kNm +(10 kN/m)\cdot 4m \cdot 2m + (10 kN)\cdot 2m + 9,4 kNm - V_{B}^{e} \cdot 4m}

\mathrm{0=86,2 kNm - V_{B}^{e} \cdot 4m}

\mathbf{V_{B}^{e}=21,6 kN}

Logo, podemos calcular a reação no primeiro apoio pelo somatório de forças verticais.

\mathrm{\sum V=-(10 kN/m)\cdot 4m -10 kN + V_{A} + V_{B}^{e}}

\mathrm{0=-50 kN + V_{A} + 21,6 kN}

\mathbf{V_{A} = 28,4 kN}

Agora, vamos analisar o segundo tramo.

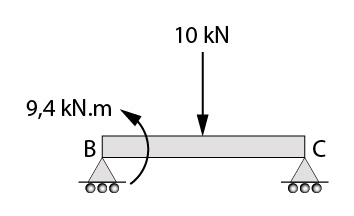
Temos que o somatório de momentos fletores para o último apoio também é igual a zero. Logo:

\mathrm{\sum M_{C}=(-10 kN)\cdot 1,5m - 9,4kNm + V_{B}^{d} \cdot 3m}

\mathrm{0=-24,4 kNm+ V_{B}^{d} \cdot 3m}

\mathbf{V_{B}^{d}=8,1 kN}

Por fim, podemos calcular a reação no último apoio pelo somatório de forças verticais.

\mathrm{\sum V=-(10 kN) + V_{C} + V_{B}^{d}}

\mathrm{0=-(10 kN/m) + V_{C} + 8,1 kN}

\mathbf{V_{C} =1,9 kN}

Já descobrimos então as reações nos dois apoios extremos.

Para calcular a reação no apoio central, basta somarmos os valores obtidos para a reação nesse apoio para os dois tramos separadamente.

\mathrm{V_{B}=V_{B}^{e}+ V_{B}^{d}}

\mathrm{V_{B}=21,6kN+ 8,1kN}

\mathbf{V_{B}=29,7 kN}

Então, as reações de apoios calculadas para a viga contínua em questão são apresentadas no esquema abaixo.

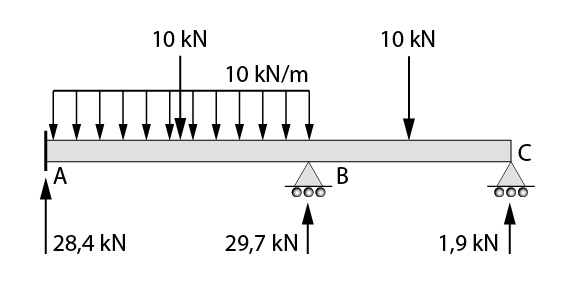
Pronto, resolvemos a questão pela equação dos três momentos. Viu como foi fácil?

Espero que você tenha entendido todo o conteúdo do post, mas caso tenha ficado alguma dúvida, deixa nos comentários que a gente responde.

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!