Equação dos três momentos: teoria

Você já aprendeu com a gente o conceito de estruturas hiperestáticas e, por isso, deve entender a dificuldade em determinar suas reações de apoio.

Porém, algumas dessas estruturas, embora usuais, tem modelos estruturais simples, como é o caso de vigas contínuas!

Para vigas contínuas podemos utilizar alguns métodos simplistas para a determinação das reações de apoio. Nesse post apresentaremos um desses métodos, conhecido com equação dos três momentos. Através dessa equação você poderá resolver de maneira mais direta vigas contínuas hiperestáticas.

Prometo que ao final do post você não terá mais nenhum problema com esse tipo de estruturas!

Vamos lá?

Equação dos três momento: modelo estrutural

Como já citado anteriormente, a equação dos três momentos foi desenvolvida para a resolução de vigas contínuas hiperestáticas com apoios inderfomáveis, conforme figura abaixo:

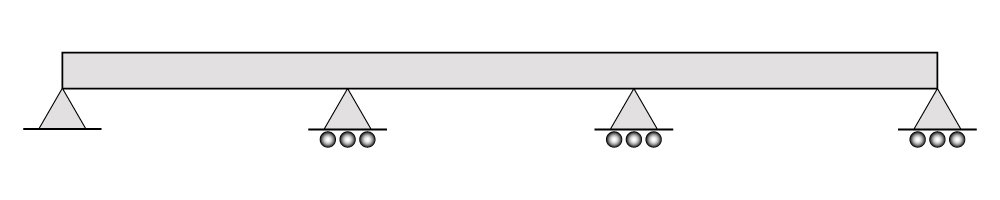
Tal equação foi desenvolvida por Clayperon através da análise dos ângulos formados entre a linha elástica da viga e os apoios intermediários, como você verá mais a frente no desenvolvimento da equação.

A utilização da equação é bem simples e consiste basicamente em considerar como incógnitas os momentos fletores em cada apoio intermediário. Para cada apoio intermediário, devemos utilizar a equação dos três momentos, de forma que ao final, o número de equações que teremos será igual ao número de incógnitas e, assim, podemos determinar tais momentos fletores através de um sistema de equações lineares.

Desenvolvimento da equação dos três momento

Para fazermos o desenvolvimento da equação dos três momentos, iremos considerar o seguinte sistema estrutural abaixo. Foi considerado que todos os carregamentos são positivos. Além disso, as formulações apresentadas são válidas apenas para vigas com momento de inércia e módulo de elasticidade constantes ao longo de cada vão.

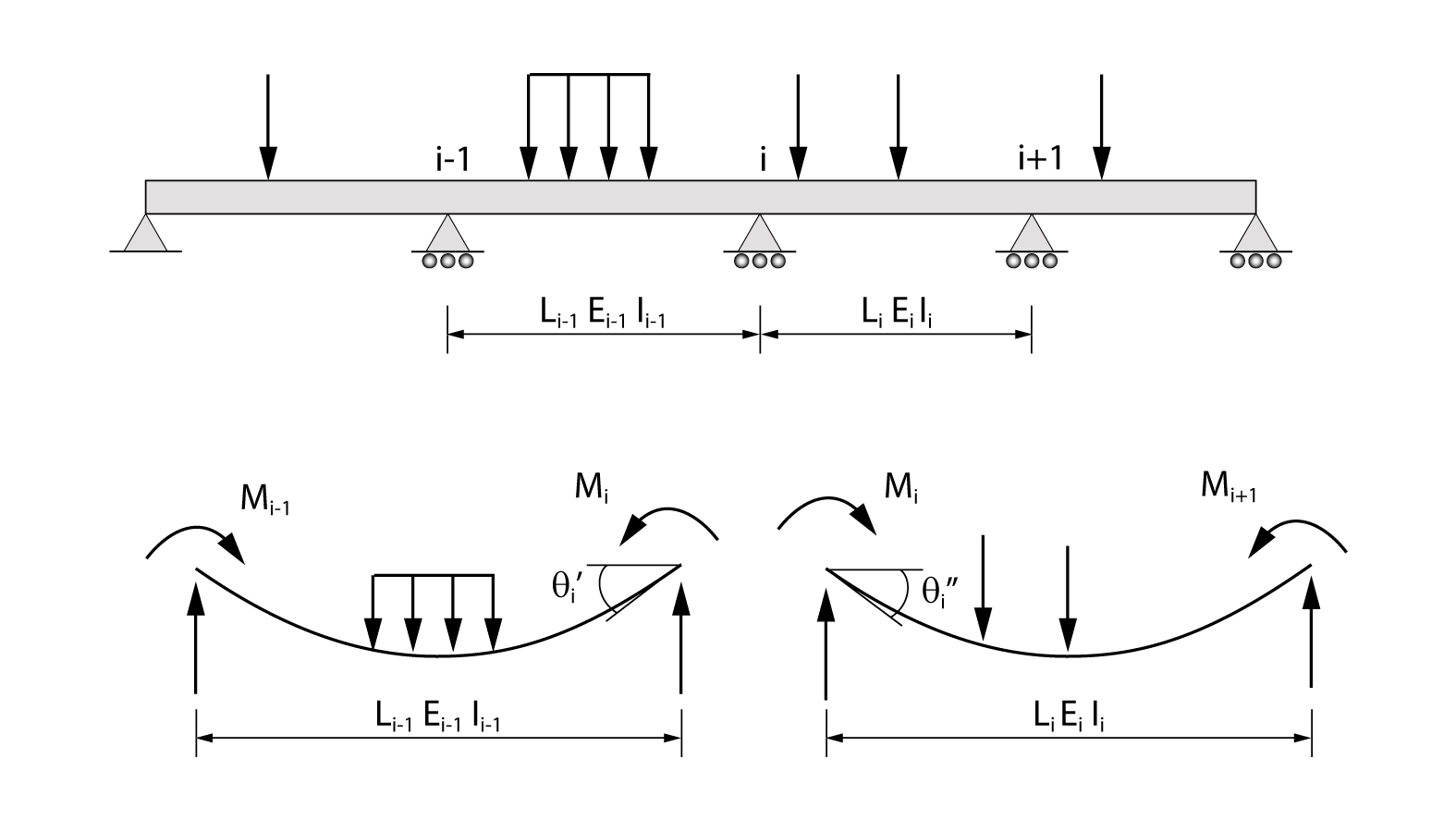
Conforme a figura apresentada, podemos inferir que a rotação \mathrm{\displaystyle\theta^{'}_{i}} é ocasionada pelos momentos nas extremidades da barra, \mathrm{\displaystyle M_{i-1}} e \mathrm{\displaystyle M_{i}}, e pelo carregamento externo ao longo da barra.

Através do “método das integrações diretas” é possível calcular a rotação relacionada a cada um desses esforços, chegando aos seguintes resultados:

O contribuição da rotação por \mathrm{\displaystyle M_{i-1}} vale:

\mathrm{\displaystyle\dfrac {M_{i-1} L_{i-1}}{6E_{i-1}I_{i-1}}}

Já a contribuição por parte de \mathrm{\displaystyle M_{i}} vale:

\mathrm{\displaystyle\dfrac {M_{i} L_{i-1}}{3E_{i-1}I_{i-1}}}

E, por fim, a contribuição do carregamento externo ao longo da barra, podemos considerar como sendo:

\mathrm{\displaystyle\dfrac {C1}{E_{i-1}I_{i-1}}}

Portanto, pela superposição de efeitos, podemos dizer que a rotação no apoio, pelo lado esquerdo, tem valor numérico:

\mathrm{\displaystyle\theta^{'}_{i}=\dfrac {M_{i-1} L_{i-1}}{6E_{i-1}I_{i-1}}+\dfrac {M_{i} L_{i-1}}{3E_{i-1}I_{i-1}}+\dfrac {C1}{E_{i-1}I_{i-1}}}

Ou

\mathrm{\displaystyle\theta^{'}_{i}=\dfrac {M_{i-1} L_{i-1}+2{M_{i} L_{i-1}}+6C1}{6E_{i-1}I_{i-1}}}

Por analogia, podemos inferir que a rotação no apoio pelo lado direito:

\mathrm{\displaystyle\theta^{''}_{i}=\dfrac {M_{i+1} L_{i}+2{M_{i} L_{i}}+6C2}{6E_{i}I_{i}}}

Onde:

• C2 é uma constante relativa ao carregamento da barra do lado direito do apoio analisado.

Abaixo, apresentaremos tabelas de C1 e C2 para vários tipos de carregamento.

Agora, continuando a dedução da equação dos três momentos, podemos dizer que, para uma viga contínua:

\mathrm{\displaystyle\theta^{'}_{i}=-\theta^{''}_{i}}

Logo:

\mathrm{\dfrac {M_{i-1} L_{i-1}}{6E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i-1}}{6E_{i-1}I_{i-1}}+\dfrac {6C1}{6E_{i-1}I_{i-1}}=-\dfrac {M_{i+1} L_{i}}{6E_{i}I_{i}}-\dfrac {2M_{i} L_{i}}{6E_{i}I_{i}}-\dfrac {6C2}{6E_{i}I_{i}}}

Através de um simples reajuste dos termos, chegamos a equação dos três momentos:

\mathrm{\dfrac {M_{i-1} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i-1}}{E_{i-1}I_{i-1}}+\dfrac {2M_{i} L_{i}}{E_{i}I_{i}}+\dfrac {M_{i+1} L_{i}}{E_{i}I_{i}}=-6\left(\dfrac{C1}{E_{i-1}I_{i-1}}+\dfrac {C2}{E_{i}I_{i}}\right)}

Essa é a famosa equação dos três momentos que, embora possa parecer complexa, nós veremos que na sua utilização é simples e ela facilita muito a resolução de vigas contínuas.

Caso especial

Agora que você já entendeu a dedução da equação dos três momentos, você percebe que ela varia basicamente com os comprimentos dos vãos, carregamentos aplicados, material (módulo de elasticidade) e geometria da barra (momento de inércia).

Mas pense bem, e se por acaso tivermos uma viga contínua com um engaste em um dos extremos?

Bem, vamos pensar juntos um pouco. O que significa um engaste?

O engaste nada mais é do que a restrição de movimento nas três direções, ou seja, não haverá rotação da barra nesse ponto!

Então, o que podemos fazer para simular essa situação?

Simples! Basta considerar um novo vão lateral a esse, com uma inércia infinita e com qualquer comprimento diferente de zero. Isso fará com que a rotação nesse ponto tenda a zero e, assim, podemos resolver também esse tipo de problema utilizando a equação dos três momentos!

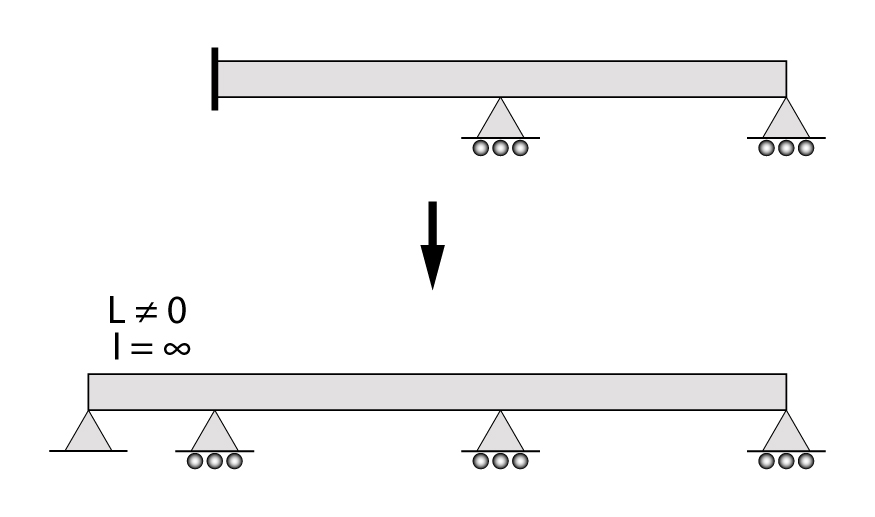
Cálculo das reações de apoio

Agora que já vimos como calcular os momentos fletores nos apoios da nossa viga contínua, você pode se perguntar: então, como eu calculo as reações de apoio?

Essa parte é bem simples!

Para o cálculo das reações, vamos utilizar cada tramo de viga separadamente, ou seja, vamos analisar um tramo (com dois apoios) por vez.

Através do somatório de momentos fletores para cada apoio, é possível determinar as reações de apoio em cada tramo.

Para o caso de apoios intermediários, ou seja, que irão constar em dois tramos, basta somarmos as reações obtidas para cada tramo isolado e, assim, determinamos a reação de apoio do mesmo!

Viu como é bem simples?

Caso tenha ficado com dificuldade para entender a aplicação dessa equação ou mesmo de como calcular tais reações de apoio, fique tranquilo, temos um post com alguns exercícios utilizando essa formulação e tenho certeza que você irá entender!

Você entendeu todo o conteúdo desse post? Caso tenha ficado alguma dúvida, deixa nos comentários que a gente responde.

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!