Superlargura para estradas: exemplo prático

No nosso post anterior sobre Superlargura, explicamos o que é e como devemos calcula-lá e distribuir na curva.  Portanto, se você ainda não leu esse post, recomendamos que dê uma rápida olhada antes de começarmos.

Agora, vamos solidificar o que foi aprendido sobre Superlargura até o momento. Para tanto, propomos um exemplo prático bem simples. Confira abaixo!

Exemplo prático

Você é responsável por um projeto rodoviário e necessita realizar a superlargura de uma curva horizontal com transição utilizando o ônibus como veículo de projeto.

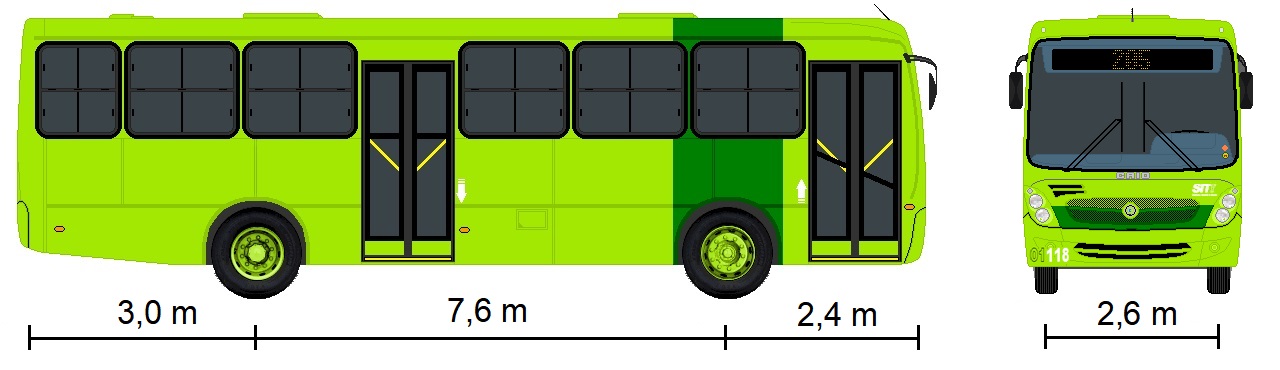
Sabe-se que o estaqueamento dessa estrada é feito a cada 20 m,  sua largura é de 6,6 m,  abaulamento de 3% e sua velocidade diretriz é 80 km/h.

DADOS ADICIONAIS DA CURVA:

• le = 170 m
• TS = 216 + 13,67 m
• SC = 225 + 3,67 m
• CS = 231 + 19,10 m
• ST = 240 + 9,10 m

RESOLUÇÃO:

Passo 01: verificar a necessidade de superlargura

O primeiro passo será verificarmos se a superelargura será necessária nesse caso. Para isso, os valores de raio mínimo para que ela seja necessária são expressos na tabela abaixo:

Tabela 1 – Valores dos raios acima dos quais é dispensável a superlargura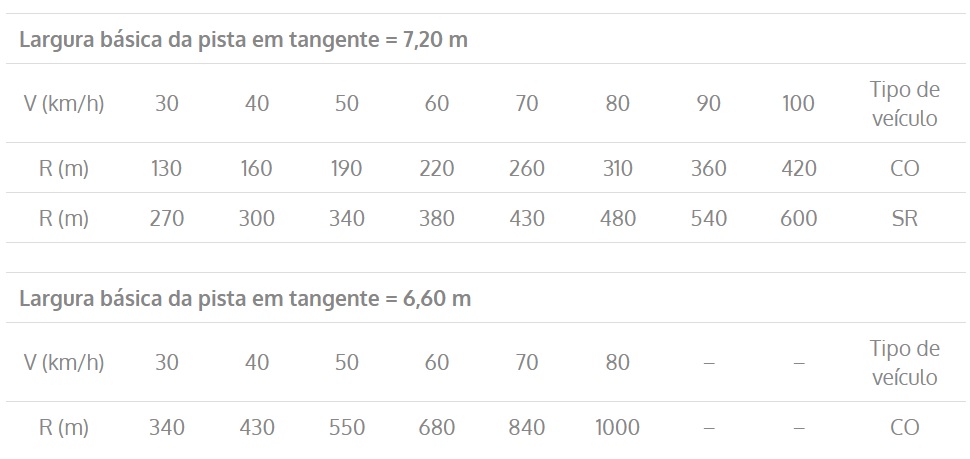

Sabemos que o nosso veículo de projeto é um ônibus e se enquadra na categoria CO (veículo comercial rígido). Além disso, a largura básica da pista é 6,6 m, a velocidade diretriz é 80 km/h e o raio é 500 m.

Desse modo, o raio máximo para a superlargura nessa estrada é 1000 m  > 500 m. Então podemos afirmar que a superlargura para essa curva será necessária.

Passo 02: Calcular a superlargura

Para o cálculo da superlargura iremos precisar das dimensões do veículo de projeto, do valor da folga lateral (tabela abaixo) e das características da pista.

Tabela 2 – Valores da folga lateral do veículo

De posse de todas as informações necessárias, a superlargura será então calculada conforme a equação abaixo, lembrando que seu valor deverá ser um múltiplo de 0,20 m:

\mathrm{S=2\left(L+\dfrac{b^2}{2R}+G_L\right)+\sqrt{R^2+F.(2b)}+...}

\mathrm{...+\dfrac{V}{10\sqrt{R}}-R-L_B}

\mathrm{S=2\left(2,6+\dfrac{7,6^2}{2.500}+0,75\right)+\sqrt{500^2+2,4.(2.7,6)}+...}

\mathrm{...+\dfrac{80}{10\sqrt{500}}-500-6,6}

\mathrm{S=0,61\:m}

\mathrm{\mathbf{S=0,60\:m}}

Passo 03: Distribuir a superlargura na curva

Agora que já calculamos a superlargura para o projeto, o próximo passo será distribuí-la ao longo da curva horizontal com transição.

Primeiro trecho: estaca TS a SC (espiral)

O primeiro trecho da distribuição é o primeiro ramo da espiral de transição, que vai da estaca TS a SC e mede le.

Dessa forma, a distribuição da superlargura nesse trecho vai de zero a S/2 (para cada lado) ao longo do comprimento le, de acordo com a equação abaixo:

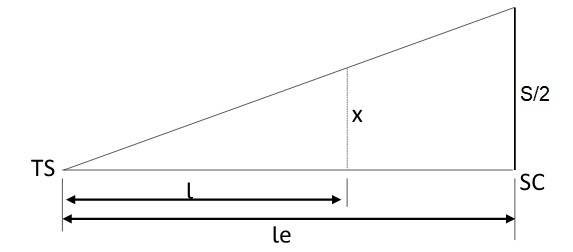
\mathrm{x=\dfrac{S}{2.le}\cdot{l}}

Além disso, nesse trecho, o estaqueamento será feito a cada 10 m, pois le >60 m.

• Estaca 216+13,67 m (TS)

\mathrm{x=\dfrac{0,60}{2.170}\cdot{0}=0,000\:m}

• Estaca 217+3,67 m

\mathrm{x=\dfrac{0,60}{2.170}\cdot{10}=0,018\:m}

• Estaca 217+13,67 m

\mathrm{x=\dfrac{0,60}{2.170}\cdot{20}=0,035\:m}

(…)

• Estaca 225+3,67 m (SC)

\mathrm{x=\dfrac{0,60}{2.170}\cdot{170}=0,300\:m} [ebook-projetos-rodoviarios]

Segundo trecho: estaca SC a CS (curva circular)

Para esse trecho não é necessário calcular a superlargura, pois ela se mantém 0,30 m para ambos os lados, da estaca SC até a estaca CS.

Terceiro trecho: estaca CS a ST (espiral)

Para esse trecho, o raciocínio é semelhante ao primeiro trecho, mas de maneira inversa. Isso quer dizer que a superlargura em cada uma das estacas desse trecho diminui até chegar a zero.

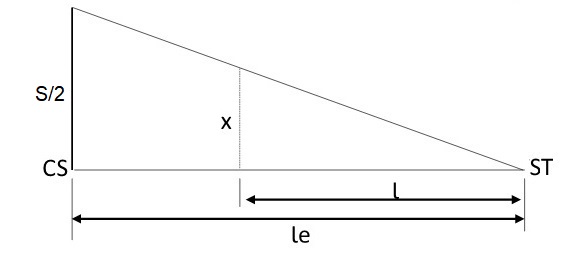
• Estaca 231+19,10 m (CS)

\mathrm{x=\dfrac{0,60}{2.170}\cdot{170}=0,300\:m}

• Estaca 232+9,10 m

\mathrm{x=\dfrac{0,60}{2.170}\cdot{160}=0,282\:m}

• Estaca 232+19,10 m

\mathrm{x=\dfrac{0,60}{2.170}\cdot{150}=0,265\:m}

(…)

• Estaca 240+9,10 m (ST)

\mathrm{x=\dfrac{0,60}{2.170}\cdot{0}=0,00\:m}

Resultado

Reunindo todos os trechos calculados anteriormente, o resultado final da distribuição da superlargura é o seguinte:

Tabela 3 – Resultado da distribuição da superlargura na curva

Estacas			Superlargura (m)
Inteira		Fracionária
TS	216	13,67 m	0,000
	217	3,67 m	0,018
	217	13,67 m	0,035
	218	3,67 m	0,053
	218	13,67 m	0,071
	219	3,67 m	0,088
	219	13,67 m	0,106
	220	3,67 m	0,124
	220	13,67 m	0,141
	221	3,67 m	0,159
	221	13,67 m	0,176
	222	3,67 m	0,194
	222	13,67 m	0,212
	223	3,67 m	0,229
	223	13,67 m	0,247
	224	3,67 m	0,265
	224	13,67 m	0,282
SC	225	3,67 m	0,300
	226		0,300
	227		0,300
	228		0,300
	229		0,300
	230		0,300
	231		0,300
CS	231	19,10 m	0,300
	232	9,10 m	0,282
	232	19,10 m	0,265
	233	9,10 m	0,247
	233	19,10 m	0,229
	234	9,10 m	0,212
	234	19,10 m	0,194
	235	9,10 m	0,176
	235	19,10 m	0,159
	236	9,10 m	0,141
	236	19,10 m	0,124
	237	9,10 m	0,106
	237	19,10 m	0,088
	238	9,10 m	0,071
	238	19,10 m	0,053
	239	9,10 m	0,035
	239	19,10 m	0,018
ST	240	9,10 m	0,000

Pois bem pessoal, essas foram algumas considerações sobre a implantação da superlargura em um projeto rodoviário, mas não para por aqui! Confira agora o super e-Book gratuito sobre Projeto Rodoviário que nós  preparamos pra você.

[ebook-projetos-rodoviarios]

É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.

Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.

Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades..

---

Fonte:

ALBUQUERQUE, Marcos. Superlargura. Teresina: UFPI, 2017.

MACEDO, Edivaldo Lins. Noções de Topografia Para Projetos Rodoviarios.  2008. Disponível em: <http://www.topografiageral.com/>. Acesso em: 12 set 2019.