Para início de conversa, superlargura é o acréscimo da largura da pista em trechos de curva com o objetivo de melhor as condições de conforto e segurança de uma estrada, principalmente quando estamos tratando de veículos de grande porte, como os caminhões.
Mas por que a utilizamos somente nas curvas?
Isso acontece porque, nos trechos em curva, os veículos ocupam fisicamente espaços laterais maiores do que as suas próprias larguras e quando maior for esse veículo maior o espaço ocupado por ele (observe a animação abaixo).
Além disso, há também a sensação natural de confinamento em trechos curvos devido aos efeitos de deformação visual e à dificuldade normalmente sentida pelo condutor de um veículo pesado por uma trajetória curva.

Até aqui você já conseguiu perceber umas semelhanças com a superelevação?
Pois bem, na maioria das vezes, a superlargura e a superelevação são usadas juntas, uma complementando a outra, com a mesma finalidade.
Então, engenheiros, neste post, iremos aprender a calcular a superlargura de uma estrada para os dois tipos de curva horizontal.
Então, antes de mais nada, recomendo que dê uma rápida olhada nos nossos posts de curva horizontal simples e com transição.
Agora, vamos lá?
Quando dispensar a superlargura
Acabamos de descobrir que a superlargura é usada em curvas horizontais para melhorar as condições de movimento do veículo.
No entanto, para curvas com raio muito grande em relação à velocidade diretriz de projeto, mesmo os veículos longos conseguem realizar a manobra com conforto e, neste caso, a superlargura pode ser dispensada.
Desse modo, os valores de raio mínimo para que seja necessário superelevação são expressos na tabela abaixo:
Tabela 1 – Valores dos raios acima dos quais é dispensável a superlargura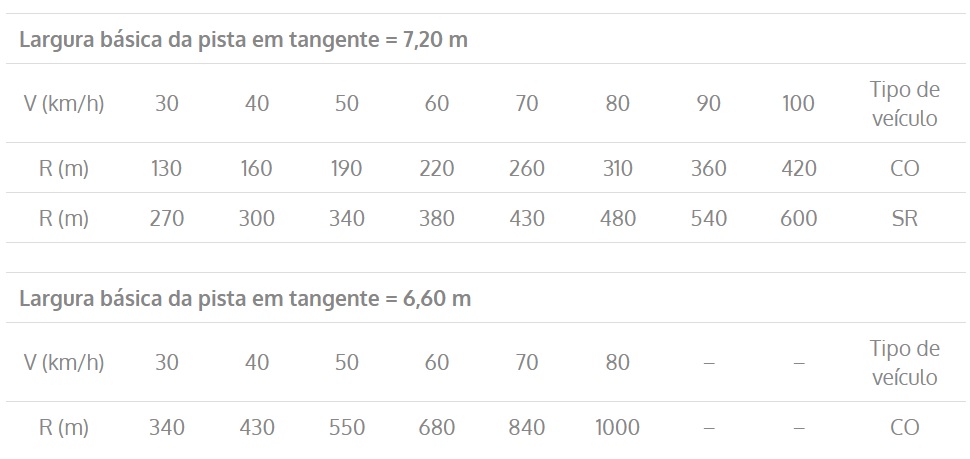
Cálculo da superlargura
Atualmente, o cálculo da superlargura utilizado pelo departamento de Estrada de Rodagem é feito através da formulação abaixo, que considera a largura total da pista necessária no trecho curvo para um dado veículo de projeto:
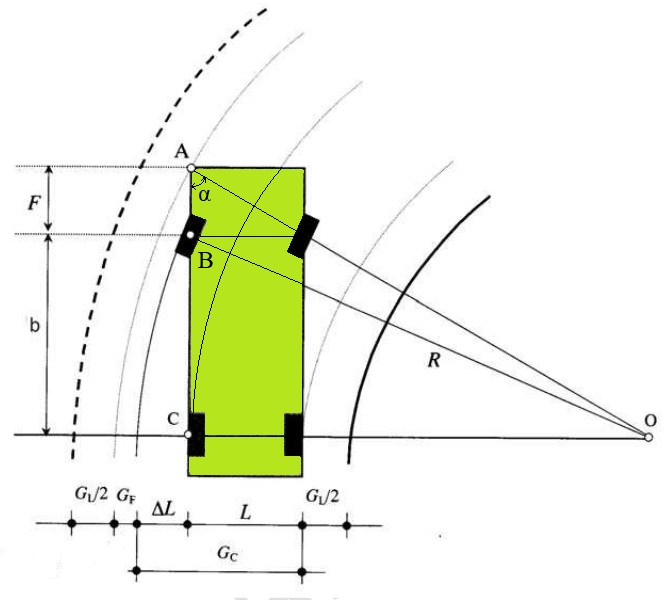
\mathrm{S=2\left(L+\dfrac{b^2}{2R}+G_L\right)+\sqrt{R^2+F.(2b)}+\dfrac{V}{10\sqrt{R}}-R-L_B}
Onde:
- S é a superlargura (m), S ≥ 0,40 m;
- L é a largura física do veículo (m);
- b é a distância entre eixos (m);
- F é a balanço direito do veículo (m);
- R é a raio da curva (m);
- V é a velocidade diretriz (km/h);
- GL é a folga lateral do veículo em movimento (m), tabela 2;
- LB é a largura básica da pista em tangente (m).
Tabela 2 – Valores da folga lateral do veículo
O valor encontrado na equação acima é adotado apenas para pistas simples com duas faixas de rolamento. No entanto, podemos utilizar esse valor para outras pistas utilizando o seguinte multiplicador:
- 1,25 para pistas com 3 faixas;
- 1,50 para pistas com 4 faixas.
Além do mais, os valores de superlargura calculados deverão sempre ser arredondados para um múltiplo de 0,20 m, lembrando que valores menores que 0,40 m podem ser desprezados.
[ebook-projetos-rodoviarios]Distribuição da superlargura na curva
Agora que já aprendemos como calcular a superlargura recomendada para o seu projeto, o próximo passo é saber como distribuí-la ao longo da curva horizontal, seja ela simples ou com transição.
Curva horizontal simples
Para começarmos a distribuição da superlargura na curva simples, precisamos separá-la em alguns trechos.
Para isso, iremos arbitrar P como sendo a estaca de início da superlargura da curva horizontal simples e P’, a estaca de fim. Arbitraremos também os pontos A e B como sendo as estaca de início e fim da superlargura máxima recomendada, respectivamente.
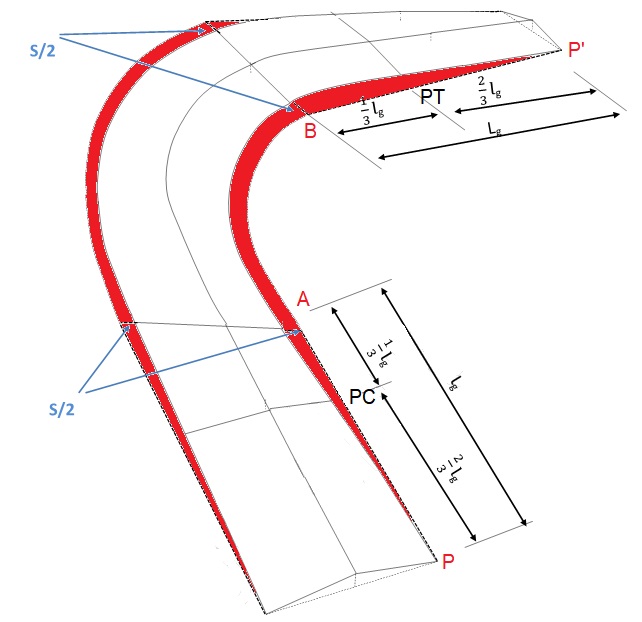
Primeiro trecho: estaca P a A
O primeiro trecho começa na estaca P e vai até a estaca A e mede o equivalente a lg, que é o comprimento do trecho do giro da plataforma e pode ser calculado por:
\mathrm{lg=\left(\dfrac{a}{g}+\dfrac{e}{2.g}\right)\cdot{L}}
Onde:
- lg é o comprimento do trecho do giro da plataforma (m);
- a é o abaulamento do trecho em tangente (%);
- eR é a superelevação máxima recomendada (%);
- g é a declividade longitudinal da borda externa (%), tabela 5;
- L é a largura da pista de rolamento (m).
Tabela 5 – Declividade longitudinal da borda da pista no trecho do giro
Desse modo, as estaca P e A que arbitramos podem ser encontradas através das equações abaixo:
\mathrm{P=PC-\dfrac{2.lg}{3}}
\mathrm{A=PC+\dfrac{lg}{3}}
Encontrados as estacas de início e fim do primeiro trecho, podemos distribuir a superlargura, lembrando a inclinação das faixas da estrada se comportam da seguinte forma:
O primeiro trecho da distribuição é o primeiro ramo da espiral de transição, que vai da estaca TS a SC e mede le.
Dessa forma, a distribuição da superlargura nesse trecho vai de zero a S/2 (para cada lado) ao longo do comprimento le, de acordo com a equação abaixo:

\mathrm{x=\dfrac{S}{2.le}\cdot{l}}
Onde:
- x é a superlargura em qualquer ponto do trecho (m);
- S é a superlargura da pista (m);
- le é o comprimento do trecho em espiral (m);
- l é a distância de um ponto em relação ao TS (m).
Segundo trecho: estaca A a B (meio do curva)
No meio da curva circular, ou seja, entre as estacas A e B, a superlargura da pista é constante, máxima e igual a S/2 para cada lado.
Como já conhecemos a estaca de início do trecho (A), basta agora calcularmos a estaca final, que se dá pela equação abaixo:
\mathrm{B=TC-\dfrac{2.lg}{3}}
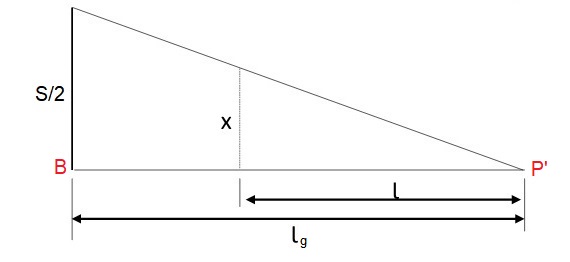
Terceiro trecho: estaca PT a P’ (tangente)
Por fim, para o trecho final da distribuição, a situação é similar ao primeiro trecho, mas de maneira inversa.
Curva horizontal com transição
Para começarmos a distribuição da superlargura na curva com transição, precisamos também separá-la em alguns trechos, conforme abaixo.
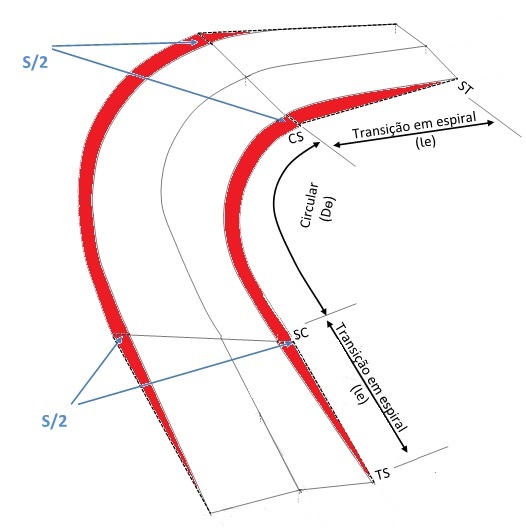
Primeiro trecho: estaca TS a SC (espiral)
O primeiro trecho da distribuição é o primeiro ramo da espiral de transição, que vai da estaca TS a SC e mede le.
Dessa forma, a distribuição da superlargura nesse trecho vai de zero a S/2 (para cada lado) ao longo do comprimento le, de acordo com a equação abaixo:
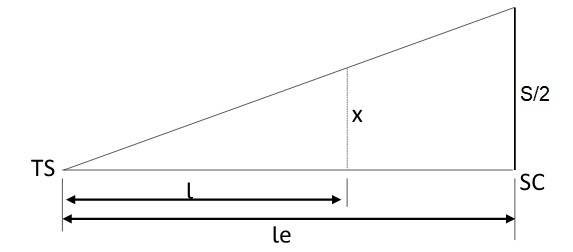
\mathrm{x=\dfrac{S}{2.le}\cdot{l}}
Onde:
- x é a superlargura em qualquer ponto do trecho (m);
- S é a superlargura da pista (m);
- le é o comprimento do trecho em espiral (m);
- l é a distância de um ponto em relação ao TS (m).
Segundo trecho: estaca CS a CS (curva circular)
Para esse trecho a superlargura é igual e constante para ambos os lados da pista e igual a S/2.
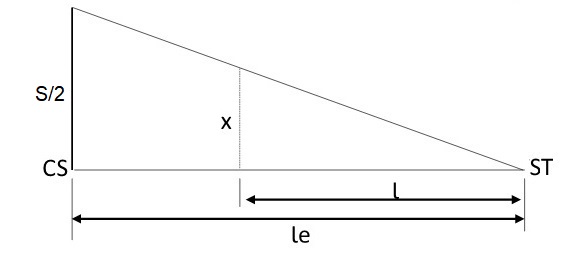
Terceiro trecho: estaca CS a ST (espiral)
Para esse trecho, o raciocínio é semelhante ao primeiro trecho, mas de maneira inversa. Isso quer dizer que a superlargura em cada uma das estacas desse trecho diminui até chegar a zero.
Pois bem pessoal, essas foram algumas considerações a respeito da superlargura, mas não para por aqui! Confira agora o super e-Book GRATUITO sobre Projeto Rodoviário que preparamos pra você.
[ebook-projetos-rodoviarios]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação em Estradas de um dos nosso parceiros, o Grupo HCT, que é um centro de aperfeiçoamento profissional atuante na área tecnológica desde 1997.
Dito isso, ficamos por aqui e se gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
Fonte:
ALBUQUERQUE, Marcos. Superlargura. Teresina: UFPI, 2017.
MACEDO, Edivaldo Lins. Noções de Topografia Para Projetos Rodoviarios. 2008. Disponível em: <http://www.topografiageral.com/>. Acesso em: 27 set 2019.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.