Cálculo de flecha em viga pelo método da linha elástica

Ao se projetar uma viga, é essencial prever as deformações (flechas) de seu eixo longitudinal que serão causadas pela atuação de cargas transversais. Essas deformações podem ser calculadas por vários métodos. Neste texto, vamos nos ater à explicação de apenas um deles: o método da linha elástica.

A linha elástica é a configuração geométrica de deslocamento vertical dos pontos situados no eixo longitudinal de uma viga, e pode ser representada analiticamente por meio de uma função y=f(x). É possível deduzir essa função a partir de uma equação diferencial ordinária de segundo grau.

Dedução da equação diferencial da linha elástica a partir da relação entre a curvatura e o momento fletor

O momento fletor atuante M e a curvatura da viga k estão relacionados de acordo com a seguinte fórmula:

\mathrm{k=\dfrac { 1 }{ \rho } =\dfrac { M }{ E\cdot I }}  (1)

onde ρ é o raio de curvatura, E é o módulo de elasticidade e I o momento de inércia.

É importante se atentar à convenção de sinais, pois a curvatura da viga fletida relaciona-se com o sentido dado aos eixos coordenados. Quando se supõe que o eixo x é positivo para a direita e que o y é positivo para baixo, como se vê na figura a seguir, admite-se que a curvatura da viga seja positiva, se a viga fletida for côncava para baixo e negativa se for côncava para cima.

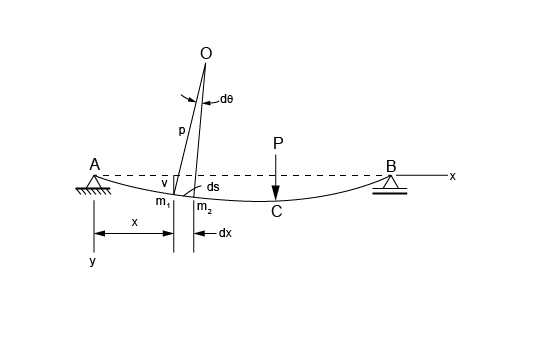
Adota-se a convenção de sinais em que o momento fletor M é positivo quando produz compressão nas fibras superiores da viga. Logo, um momento fletor positivo produz curvatura negativa, enquanto um momento fletor negativo produzirá curvatura positiva na viga.

Portanto, a equação (1) se altera da seguinte forma:

\mathrm{k=\dfrac { 1 }{ \rho } =-\dfrac { M }{ E\cdot I }} (2)

Sabendo que a curvatura k é a taxa de variação do ângulo θ com relação à distância ds medida sobre a linha elástica, sendo θ o ângulo formado pela tangente à linha elástica num determinado ponto com o eixo x; temos:

\mathrm{k=\dfrac { 1 }{ \rho } =\dfrac { d\theta }{ ds }} (3)

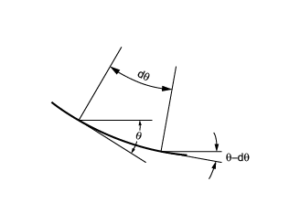
Como na maioria das aplicações práticas ocorrem apenas pequenas deflexões nas vigas, as linhas elásticas são muito achatadas e tanto o ângulo θ quanto a inclinação da curva são quantidades muito pequenas. Isso significa que podemos fazer

\mathrm{ds\simeq dx \; \therefore \; \theta \simeq tan\theta =\dfrac { dy }{ dx }}  ,

onde v é a deflexão da viga a partir de sua posição inicial.

Substituindo essas expressões na equação (3), temos:

\mathrm{k= \dfrac { 1 }{ ρ } =\dfrac { dθ }{ dx } = \dfrac { d^{ 2 }v }{ dx^{ 2 } } }.

Finalmente, combinando com a equação (2), temos:

\mathrm{\dfrac { d^{ 2 }v }{ dx^{ 2 } } = - \dfrac { M }{ EI }} (4).

E pronto, esta é a equação diferencial básica para a linha elástica de uma viga. Para cada caso particular, deve-se integrar esta equação duas vezes para obter a deflexão v, calculando-se também uma expressão generalizada para o momento fletor no trecho, M, que dependerá do tipo de viga e do carregamento.

Cálculo da fórmula da deflexão para viga biapoiada sujeita a carregamento distribuído uniformemente

Vamos calcular a equação da linha elástica para uma viga biapoiada sujeita a um carregamento uniformemente distribuído, como a da figura abaixo.

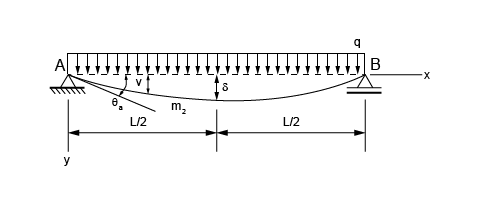
A primeira coisa a fazer é calcular a expressão generalizada para o momento fletor atuante. Sendo a taxa do carregamento q e L o comprimento total da viga, as equações fundamentais da estática nos permitem concluir que as reações nos apoios são iguais e equivalentes a \frac { qL }{ 2 }  . Logo, o momento fletor atuante em um ponto situado a uma distância x do apoio da esquerda é dado pela fórmula:

\mathrm{M=\dfrac { qLx }{ 2 } -\dfrac { q{ x }^{ 2 } }{ 2 }} (5),

ainda de acordo com a convenção que estabelece o momento fletor atuante positivo como aquele que traciona as fibras inferiores da viga.

Substituindo a equação (5) na expressão (4) encontrada anteriormente, temos:

\mathrm{EIv"=-\dfrac { qLx }{ 2 } +\dfrac { q{ x }^{ 2 } }{ 2 }} (6).

Multiplicando-se ambos os membros desta equação por dx e integrando, temos:

\mathrm{EIv'=-\dfrac { qL{ x }^{ 2 } }{ 4 } +\dfrac { q{ x }^{ 3 } }{ 6 } + C_1} (7),

onde C1 é uma constante de integração. Antes de prosseguirmos, é importante salientar que a equação diferencial de primeira ordem rege a variação da declividade ao longo da viga, isto é, a rotação das seções da viga com relação ao eixo tangencial à seção. Por exemplo, na figura acima, o ângulo θa é a declividade na seção do apoio A.

De posse dessa informação e observando-se, pela simetria, que a inclinação da curva elástica no meio do vão é zero, temos a seguinte condição:

\mathrm{v' = 0} quando \mathrm{x = \dfrac{L}{2}}

Fazendo as devidas substituições na equação (7), encontramos que o valor de C1 é igual a\mathrm{\dfrac { q{ L }^{ 3 } }{ 24 }}, o que transforma a equação (7) em:

\mathrm{EIv'=-\dfrac { qL{ x }^{ 2 } }{ 4 } +\dfrac { q{ x }^{ 3 } }{ 6 } +\dfrac { q{ L }^{ 3 } }{ 24 }} (8)

Multiplicando-se novamente ambos os membros da equação por dx e integrando, temos:

\mathrm{EIv=-\dfrac { qL{ x }^{ 3 } }{ 12 } +\dfrac { q{ x }^{ 4 } }{ 24 } +\dfrac { q{ L }^{ 3 }x }{ 24 } + C2} (9)

A constante de integração C2 pode ser encontrada porque sabemos que a linha elástica não sofre deflexão nos apoios, ou seja, v =0 quando x = 0; o que resulta em C2 = 0.

Finalmente, reorganizando a equação (9), temos:

\mathrm{v=\dfrac { qx({ L }^{ 3 }-2L{ x }^{ 2 }+{ x }^{ 3 }) }{ 24EI }} (10),

que nos permite encontrar a deflexão em qualquer ponto ao longo da viga.

O valor máximo, representado por δ, ocorre no meio do vão e é obtido substituindo x na equação (10) por L/2:

\mathrm{δ=\dfrac { 5q{ L }^{ 4 } }{ 384EI }} (11).

Já a inclinação máxima ocorre nas extremidades da viga. Fazendo x=0 na equação (8), para a extremidade esquerda, temos:

\mathrm{θa=\dfrac { q{ L }^{ 3 } }{ 24EI }} (12).

Exemplo aplicado

Utilizando a fórmula 11, vamos encontrar a deflexão no meio do vão de uma viga de concreto biapoiada de comprimento L = 3 m, carregamento q = 10 kN/m, módulo de elasticidade E = 21287 MPa e seção retangular de 15 cm de largura por 30 cm de altura.

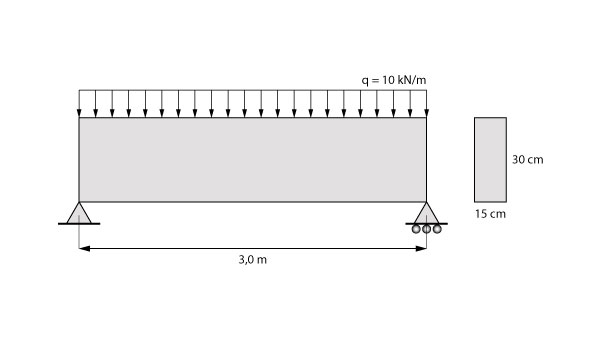
Para a resolução dessa questão, iremos trabalhar com tudo em kN e cm. Dessa forma, o módulo de elasticidade vale \mathrm{E = 2128,7 \; kN / cm^2} e o carregamento \mathrm{q = 0,1 \; kN / cm}

 

Calculando o momento de inércia da seção retangular:

\mathrm{I = \dfrac{15 \cdot 30^3}{12} = 33750 \; cm^4}

Dessa forma, temos que a deflexão no centro do vão é igual a:

\mathrm{δ=\dfrac { 5 \cdot 0,1 \cdot { 300 }^{ 4 } }{ 384 \cdot 2128,7 \cdot 33750 }= 0,147 \; cm}

\mathrm{δ = 1,47 \; mm}

Gostou do nosso post? Ficou curioso para aprender mais? Caso queira aprofundar seu conhecimento, indico o livro de Resistência dos Materiais do Hibbeler. Um material completo e intuitivo, que com certeza agregará bastante!

Ainda ficou com alguma dúvida? Deixe nos comentários abaixo!