Nesse post iremos resolver exercícios sobre os índices físicos do solo!
Então, se prepare para aprender, na prática, os conceitos apresentados no post anterior.
Vamos resolver questões tentando utilizar todos os 8 principais índices físicos citados no post anterior!
Agora, sem mais delongas, vamos à resolução dos exercícios.
Exemplo 1
Considere uma amostra de solo seco com índice de vazios e=0,6 e peso específico dos grãos \mathrm{\gamma_{g}=24 kN/m^3}. Determine:
a. Seu peso específico natural;
b. Considerando que tal solo foi umedecido até chegar a um grau de saturação S=70% sem modificar o índice de vazios, qual seria seu novo teor de umidade e seu novo peso específico natural?
Resolução
Então, como você pode perceber, na resolução dessa questão iremos utilizar os conceitos de:
- Umidade do solo (h);
- Peso específico natural (\mathrm{\gamma})e dos grãos (\mathrm{\gamma_g});
- Índice de vazios (e);
- Grau de saturação (S).
Logo, vamos resolver inicialmente o item a.
Resolução item a.
Para isso, lembremos do conceito de índice de vazios:
\mathrm{e=\dfrac{V_v}{V_s}}
Nós sabemos também que:
\mathrm{e=\dfrac{V_v}{V_s}}
Logo, relembrando do sistema trifásico do solo, temos que:
\mathrm{V_t=V_v+V_s}

Então, adotando que o o volume de sólidos da amostra é de 1 m³, temos que:
\mathrm{V_v=0,6m^3}, logo, \mathrm{V_t=1,6m^3}
Entretanto, o enunciado da questão já nos afirma que se trata de um solo seco. Então, como não possui água no solo, o peso total do solo é igual ao peso dos grãos.
\mathrm{\gamma_g=\dfrac{P_s}{V_s}}
\mathrm{24=\dfrac{P_s}{1m^3}}
\mathrm{P_s=24 kN}
Por fim, podemos afirmar que o peso específico natural do solo é:
\mathrm{\gamma=\dfrac{P_t}{V_t}}
\mathrm{\gamma=\dfrac{24 kN}{1,6m^3}}
\mathrm{\gamma=15 kN/m^3}
OBS: Lembrando que fizemos assim para mostrar que você pode resolver essa questão apenas com os conhecimentos dos conceitos do índices físicos. Entretanto, se você já leu nosso post anterior, viu que poderia simplesmente utilizar a seguinte formulação:
\mathrm{e=\dfrac{\gamma_g}{\gamma_s}-1}
\mathrm{0,6=\dfrac{24}{\gamma_s}-1}
\mathrm{\gamma_s=15 kN/m^3}
Vale ressaltar novamente que, como o solo é seco, \mathrm{\gamma_s=\gamma}.
Resolução item b.
No item b. a situação já é um pouco diferente, pois o solo não é mais seco!
Então, precisamos nos lembrar dos conceitos de grau de saturação (S) e de umidade do solo (h).
\mathrm{S\%=\dfrac{V_a}{V_v}\cdot 100}
Como a questão nos afirma que S=70%, temos que:
\mathrm{V_a=0,7\cdot V_v}
Sabemos também que o índice de vazios continua sendo e=0,6 e que tanto o volume dos grãos, como o peso do grãos não sofre modificação durante esse processo de umidificação do solo.
Então, temos que para a mesma consideração de volume dos sólidos como 1m³:
\mathrm{e=\dfrac{V_v}{V_s}}
\mathrm{V_v=0,6m^3}
\mathrm{V_a=0,7 V_v=0,42 m^3}
Logo, sabendo que o peso específico da água é \mathrm{\gamma_a=10 kN/m^3}, temos que o peso de água para o solo, nessa consideração é de 4,2 kN.
Como já calculamos anteriormente, o volume total da amostra para essa consideração é de 1,6 m³.
Então temos:
\mathrm{\gamma=\dfrac{P_t}{V_t}}
\mathrm{\gamma=\dfrac{24+4,2}{1,6}}
\mathrm{\gamma=17,63 kN/m^3}
Perceba que o peso específico aparente do solo aumenta, pois foi adicionada água no mesmo.
Agora, calcularemos facilmente o teor de umidade do solo (h):
\mathrm{h=\dfrac{P_{a}}{P_{s}}}
\mathrm{h=\dfrac{4,2}{24}}
\mathrm{h=17,5\%}
Pronto! Assim, finalizamos a resolução da primeira questão!
Perceba que já precisamos envolver diversos índices físicos do solo para sua resolução. Mas agora vamos para o exercício 2.
Exemplo 2
É feito um corte com volume de 120 m3 de solo, com um índice de vazios e = 1,16. Determine qual o volume de aterro com índice de vazios e=0,75 que pode ser executado com esse solo.

Resolução
Para entendermos melhor essa questão, vamos apresentar uma representação abaixo.
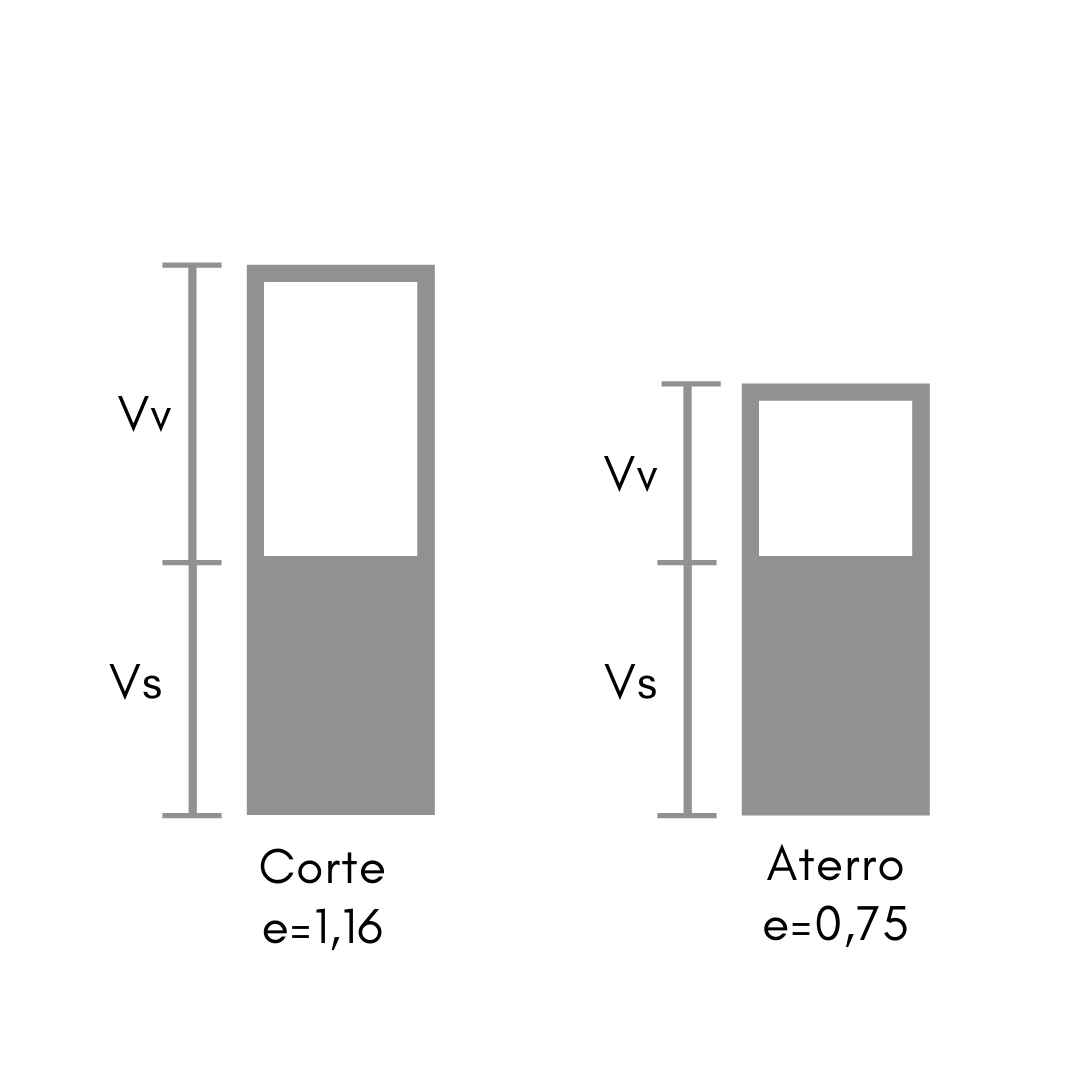
Então, perceba que o volume de sólidos não vai se modificar.
Entretanto, com a compactação, o volume de vazios vai diminuir, por isso, seu índice de vazios será alterado.
Você consegue perceber agora facilmente que o que temos como constante entre o corte e o aterro é justamente o volume e peso dos sólidos!
Como temos que o volume total do corte é de 120 m³:
\mathrm{e=\dfrac{V_v}{V_s}}
\mathrm{1,16=\dfrac{120-V_s}{V_s}}
\mathrm{V_s=55,6 m^3}
Então, para o aterro, teremos:
\mathrm{e=\dfrac{V_v}{V_s}}
\mathrm{0,75=\dfrac{V_v}{55,6}}
\mathrm{V_v=41,7 m^3}
Logo:
\mathrm{V_t=V_v+V_s}
\mathrm{V_t=55,6+41,7}
\mathrm{V_t=97,3 m^3}
Ou seja, com o corte de 120m³, podemos executar um aterro de 97,3 m³ com os índices de vazios especificados na questão!
E então, está achando muito difícil? Aposto que não!
Vamos agora para o terceiro exercício!
Exemplo 3
Considere um amostra de solo com peso específico aparente natural de 1,90 g/cm³ e teor de umidade 9%. Qual o volume de água a adicionar, por metro cúbico de solo, para que o teor de umidade passe a ser 16%, considerando um índice de vazios constante durante esse processo?
Resolução
Então, essa questão também será sobre teor de umidade do solo e peso específico!
Assim como na questão anterior, temos que entre a condição final e a condição inicial temos como constante o peso e volume da parcela sólida do solo.
Vamos considerar, então, que estamos trabalhando com 1 m³ desse solo.
Logo, o peso específico aparente natural do mesmo é 1.900 kg/m³, ou seja, 19 kN/m³.
Então, para 1 m³ do solo, temos \mathrm{P_t=19 kN}.
Como sabemos que o teor de umidade inicial é de 9%:
\mathrm{h=\dfrac{P_{a}}{P_{s}}}
\mathrm{0,09=\dfrac{19-P_s}{P_{s}}}
\mathrm{P_s=17,43 kN}
Por consequência:
\mathrm{P_t=P_s+P_a}
\mathrm{19=17,43+P_a}
\mathrm{P_a=1,57 kN}
Então, agora que já sabemos o peso de sólidos e de água no nosso solo, precisamos calcular o peso de água na situação final.
Na situação final, temos que h=16%. Logo:
\mathrm{0,16=\dfrac{P_{a}}{17,43}}
\mathrm{P_a=2,79 kN}
Ou seja, nós precisamos adicionar 1,22 kN de água para 1 m³ de solo, que é a diferença do peso final e inicial de água no solo.
Como o exercício pede que calculemos o quanto precisamos adicionar em volume, considerando que o peso específico da água é \mathrm{\gamma_a=10 kN/m^3}, teremos que adicionar um total de 0,122m³ de água ao solo!
Pronto! Com isso nós finalizamos nosso post de exercícios resolvidos sobre índices físicos do solo.
Eu espero que você tenha aprendido tudo e que esse post tenha sido útil pra você!
Porém, se ainda ficou com alguma dúvida, pode deixar nos comentários que vai ser um prazer te responder!
Além disso, continue seguindo nosso blog e nos acompanhando no YouTube.
Dessa forma, fico por aqui! Até a próxima =)
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

Como o Ps virou 17,43?