Os 8 principais índices físicos do solo

Se prepare que agora você vai aprender tudo sobre os índices físicos do solo!

Nesse post veremos os principais índices físicos do solo, a importância deles e como podemos calculá-los!

Então, se você sempre se confundiu com todos esses índices, essa é sua chance de aprender tudo.

Agora, sem mais delongas, vamos direto ao conteúdo.

Índices físicos: o que são?

Inicialmente, vamos tratar do conceito de índices físicos.

Os índices físicos nada mais são do que grandezas que expressam proporções de pesos e volumes entre as três fases do solo: água, sólido e ar.

Ou seja, para que você entenda bem os conceitos que vamos apresentar adiante, é importante que você entenda o sistema trifásico do solo, representado na figura abaixo.

Você pode perceber que o solo é composto de uma fração sólida (partículas), água e ar.

Além disso, perceba também que podemos trabalhar com essas fases em volume e em peso.

E para finalizar, perceba que podemos ignorar o peso do ar, embora o mesmo ocupe volume (\mathrm{V_{ar}}).

Então, a partir de agora trataremos as fases com as seguintes nomenclaturas:

• \mathrm{V_{s}} e \mathrm{P_{s}}: para o volume e peso, respectivamente, da fração sólida;
• \mathrm{V_{a}} e \mathrm{P_{a}}: para o volume e peso, respectivamente, da fração de água;
• \mathrm{V_{ar}} : para o volume de ar;
• \mathrm{V_{t}} e \mathrm{P_{t}}: para o volume e peso totais do solo.

E agora que você já entende a representação trifásica do solo, você pode me perguntas: “mas Filipe, qual a importância dos índices físicos do solo?”

Vou tentar ser bem direto! Tanto os índices físicos, como a granulometria e os limites de consistência do solo são importantes para a classificação do solo!

Isso se dá pelo fato de que tais propriedades podem ser relacionadas a diversas outras propriedades do solo, como permeabilidade, compressibilidade, resistência.

Então, agora que você já sabe o conceito dos índices físicos e sua importância, vamos falar rapidamente sobre os principais índices físicos.

Principais índices físicos

Umidade do solo (h)

A umidade do solo é simplesmente a relação entre o peso de água e o peso de sólido presente em uma amostra e é geralmente expressa em porcentagem.

\mathrm{h=\dfrac{P_{a}}{P_{s}}}

CUIDADO: É comum alunos confundirem esse conceito e acharem que umidade é uma relação entre o peso de água e o peso total da amostra. Então, tenha cuidado para não se confundir também!

Peso específico aparente do solo (\mathrm{\gamma})

Por definição, o peso específico aparente do solo é a relação entre o peso total do solo e o volume total do solo quando a umidade do solo é diferente de zero!

\mathrm{\gamma=\dfrac{P_t}{V_t}}

Em campo, podemos determinar o peso específico aparente do solo através do “frasco de areia”.

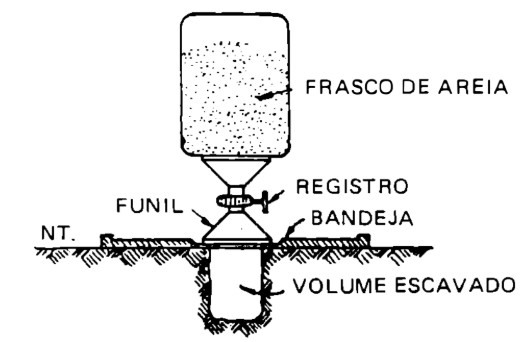
Peso específico aparente do solo seco (\mathrm{\gamma_s})

Esse índice físico apresenta o mesmo conceito do índice anterior, entretanto, para um solo seco com umidade igual a zero (h=0).

Ou seja, como não há água no solo, o peso total vai ser o peso das partículas sólidas. Logo:

\mathrm{\gamma_s=\dfrac{P_s}{V_t}}

Podemos ainda fazer uma relação entre o peso específico aparante e o peso específico aparente do solo seco:

\mathrm{\gamma_s=\dfrac{\gamma}{1+h}}

Índice de vazios (e)

Este índice físico foi primeiramente utilizado por Terzaghi para o estudo de adensamento no solo!

Por definição, o índice de vazios é a relação entre o volume vazio e o volume de sólidos presente no solo:

\mathrm{e=\dfrac{V_v}{V_s}}

A determinação do índice de vazios pode ser feita em laboratório, a partir da seguinte formulação:

\mathrm{e=\dfrac{\gamma_g}{\gamma_s}-1}

Onde:

• \mathrm{\gamma_g}: é o peso específico das partículas sólidas, ou seja, o peso específico apenas dos grãos sólidos do solo.

Porosidade (n)

Então, vamos agora falar um pouco sobre o índice de porosidade do solo.

A porosidade se assemelha muito ao índice de vazios do solo, entretanto, ela é uma razão dos vazios do solo com o volume total da amostra. Outra diferença é que a porosidade é geralmente expressa em porcentagem.

\mathrm{n\%=\dfrac{V_v}{V_t}\cdot 100}

Podemos ainda correlacionar a porosidade do solo com seu peso específico aparente seco.

\mathrm{\gamma_s=\gamma_g \cdot (1-n)}

Grau de saturação do solo (S)

O grau de saturação do solo é geralmente expresso em porcentagem e representa o volume de água contida nos vazios do solo.

\mathrm{S\%=\dfrac{V_a}{V_v}\cdot 100}

Então, podemos dizer que:

• Solo seco (S=0): quando temos o solo seco, não temos água no solo, logo, a saturação do mesmo é igual a zero!
• Solo saturado (S=100%): quando todos os vazios do solo estão preenchidos com água, temos o que chamamos de solo saturado, logo, o grau de saturação é igual a 100%.

Para um solo saturado, podemos fazer a seguinte relação entre índice de vazios e umidade:

\mathrm{e=h\cdot \dfrac{\gamma_g}{\gamma_a}}

Onde:

• \mathrm{\gamma_a}: peso específico da água.

Falando de grau de saturação, podemos ainda citar um índice de solo que não é tão usado quanto à saturação, que é o grau de aeração do solo (A).

O grau de aeração nada mais é do que a porcentagem de vazios que é ocupado por ar:

\mathrm{A\%=\dfrac{V_{ar}}{V_v}}

Ou seja, podemos dizer que:

\mathrm{A\%=100-S\%}

Por fim, vamos falar sobre os pesos específicos de solos saturados e submersos!

Peso específico de solo saturado (\mathrm{\gamma_{sat}})

Então, como já comentamos anteriormente, em um solo saturado, todo o volume vazio está preenchido por água.

É uma condição de solo bem usual na prática!

Para um solo saturado, podemos fazer relações com a porosidade do solo e com o índice de vazios do mesmo:

\mathrm{\gamma_{sat}=\gamma_s+n\cdot\gamma_a}

 

\mathrm{\gamma_{sat}=\dfrac{\gamma_g+e\cdot\gamma_a}{1+e}}

Peso específico do solo submerso (\mathrm{\gamma_{sub}})

É o peso específico de um solo que encontra-se submerso, ou seja, abaixo do nível de água.

Quando o solo está nessa condição, suas partículas sofrem empuxo da água. Então, teremos que:

\mathrm{\gamma_{sub}=\gamma_{sat}-\gamma_a}

Vale ainda notar que um solo submerso é sempre saturado, porém um solo saturado nem sempre é submerso!

 

Recado final

Então pessoal, por hoje é isso!

Espero que você tenha gostado e que tenha sido útil pra você.

Porém, se ficou com alguma dúvida, não se acanhe! Deixe seu comentário aqui embaixo que a gente responde!

Continue seguindo nosso blog e nos acompanhando no YouTube.

Dessa forma, fico por aqui! Até  a próxima =)