Hoje é dia de resolver exercícios sobre a lei de Darcy!
Se você caiu de pára-quedas nesse post, recomendo que você dê uma lida rápida no nosso post com a teoria da lei de Darcy.
Lá abordamos, além da teoria sobre a própria lei, conceitos de permeabilidade que são importantes para o melhor entendimento do conteúdo!
Agora, sem mais delongas, vamos aos exercícios!
Exemplo 1
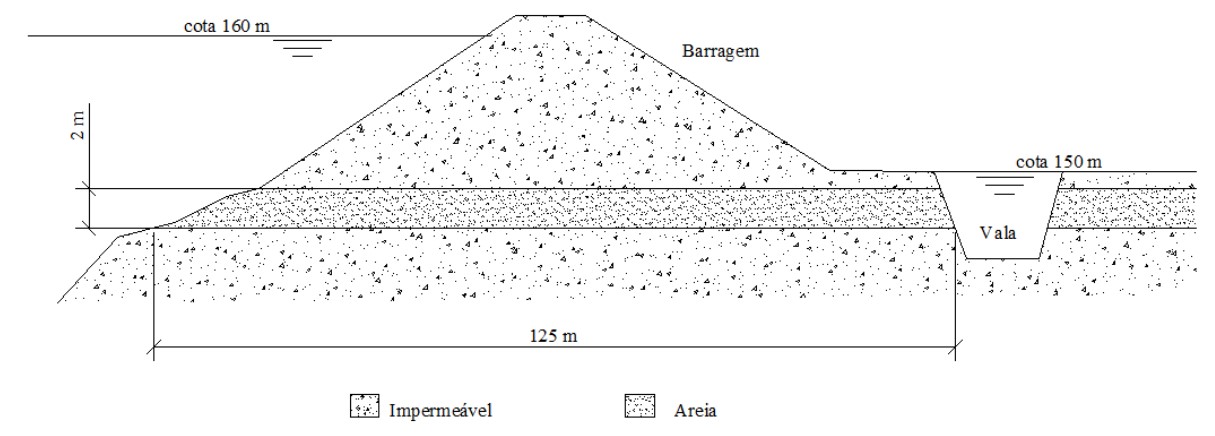
Na fundação de uma barragem foi encontrada uma camada de areia cuja seção transversal está mostrada na figura abaixo, e apresenta uma
extensão de 300m. O coeficiente de permeabilidade dessa areia é igual 3,5 m/dia. Qual o volume de água flui para a vala em 1 hora?
Resolução
Então, essa é uma questão relativamente simples de lei de Darcy, mas escolhi esse exercício simplesmente para que você possar iniciar com um nível mais básico.
Relembrando a lei de Darcy:
\mathrm{Q=k\cdot \dfrac{\Delta h}{L}\cdot A}
Onde:
- Q: vazão (m³/s);
- k: coeficiente de permeabilidade do solo (m/s);
- \mathrm{\Delta h}: diferença de altura do nível de água entre os dois “reservatórios”;
- L: comprimento da amostra de solo;
- A: área transversal a amostra de solo;
Perceba que o comprimento da barragem (300 m) é, também, a largura da camada de de areia. Então, a área da seção transversal na qual haverá fluxo de água é:
\mathrm{A=300\cdot 2=600 m^2}
Então, aplicando a lei de Darcy, temos:
\mathrm{Q=3,5 m/dia\cdot \dfrac{160m-150m}{125m}\cdot 600m^2}
\mathrm{Q=168 m^3/dia}
Tenha muito cuidado com as unidades que você trabalha! Perceba que o resultado foi dado em m³/dia devido as unidades em questão, mas não é uma unidade definitiva.
Qualquer unidade de volume/tempo é admita, visto que estamos calculando uma vazão.
Mas agora, vamos finalizar nossa questão!
O exercício determine o volume de água que flui através da barragem em 1 hora. Como determinamos o volume por dia, podemos fazer simplesmente uma regra de três:
\mathrm{\dfrac{168m^3}{24h}=\dfrac{x m^3}{1h}}
\mathrm{x=7 m^3}
Então, durante 1 hora, para os dados apresentados no exercício, vão fluir 7,0 m³ de água ao longo de toda a extensão da barragem!
Mas eu sei que você achou essa questão muito simples!
Então, agora vamos para um exercício um pouco mais complicado.
[planilha-capacidade-estacas]Exemplo 2
Um rio e um córrego tem correm um longo percurso paralelamente entre si e muito próximos um do outro. Entre eles existe uma camada de areia, conforme a figura abaixo.
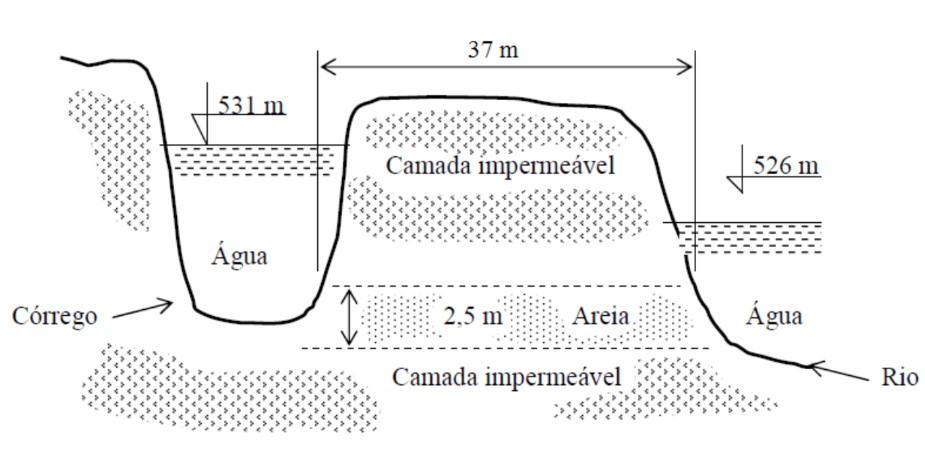
Calcule o volume que flui em 30 minutos, por metro corrido (perpendicular ao plano da figura) através dessa camada permeável de areia, sabendo que os primeiros 25 m da camada de areia possui \mathrm{k1=9\cdot 10^{-3} cm/s}, enquanto nos últimos 12 m da camada, o coeficiente de permeabilidade é 7 vezes maior que da primeira camada.
Resolução
Bem, como você percebeu, esse exercício é um pouco mais complicado que o primeiro, pois trata-se de um caso de estratificação do solo. Logo, precisamos calcular um valor de coeficiente de permeabilidade equivalente que simule as duas camadas.
Prestando atenção, perceba que o fluxo de água ocorre da esquerda em uma direção que é perpendicular à estratificação do solo!
Então, utilizaremos a fórmula, já apresentada no post com a teoria da lei de Darcy, para cálculo do coeficiente de permeabilidade equivalente para esse caso:
\mathrm{\dfrac{L}{k_{eq}}=\dfrac{L_1}{k_1}+\dfrac{L_2}{k_2}+...+\dfrac{L_n}{k_n}}
No nosso exercício, temos apenas 2 camadas de solo. Além disso, sabemos que a segunda camada possui um coeficiente de permeabilidade 7x maior que o da primeira camada. Logo:
\mathrm{k_2=7 \cdot 9\cdot 10^{-3}=63\cdot 10^{-3} cm/s}
Agora, calculando o coeficiente de permeabilidade equivalente das duas camadas, temos:
\mathrm{\dfrac{37m}{k_{eq}}=\dfrac{25m}{9\cdot 10^{-3}cm/s}+\dfrac{12m}{63\cdot 10^{-3} cm/s}}
Para que não haja nenhum equívoco futuro com as unidades utilizadas, vamos transformar as unidades de comprimento para metro:
\mathrm{\dfrac{37m}{k_{eq}}=\dfrac{25m}{9\cdot 10^{-5}m/s}+\dfrac{12m}{63\cdot 10^{-5} m/s}}
\mathrm{k_{eq}=12,47\cdot 10^{-5} m/s}
Agora que já calculamos o coeficiente de permeabilidade equivalente, podemos utilizar a lei de Darcy.
\mathrm{Q=k\cdot \dfrac{\Delta h}{L}\cdot A}
\mathrm{Q=12,47\cdot 10^{-5} \cdot \dfrac{531-526}{37}\cdot 2,5\cdot 1}
Perceba que a área calculada foi para 1 metro de largura da camada, já que é o que a questão pede.
Perceba também que todas as unidades de comprimento (que foram suprimidas) estão em metro. Logo:
\mathrm{Q=4,21\cdot 10^{-5} m^3/s}
Então, agora que já temos a vazão, basta calcularmos o volume que flui por essa camada em 30 minutos, como pede a questão.
Fazendo uma regra de três simples, temos:
\mathrm{\dfrac{4,21\cdot 10^{-5}}{1s}=\dfrac{x}{1800 s}}
\mathrm{x=7,58\cdot 10^{-2}m^3}
Ou, se quisermos apresentar o resultado em litros:
\mathrm{x=75,8 l}
Então, durante 30 minutos, vão fluir 75,8 l de água do córrego para o rio pela camada permeável de areia que liga os dois!
Recado final
Viu como não foi tão difícil assim? =)
Nesse post, apresentei e resolvi com você dois exercícios sobre lei de Darcy.
Nos exercícios, além de discutirmos um pouco sobre os conceitos de permeabilidade, conseguimos pôr em prática os conteúdos abordados no post com a teoria do assunto.
Então, acredito que agora você já tenha uma noção da importância da lei de Darcy e da permeabilidade do solo para algumas áreas da engenharia.
Espero que esse post tenha sido útil e que você tenha aprendido tudo o que quis passar de conhecimento!
Mas, caso ainda tenha alguma dúvida, pode deixar nos comentários que vai ser um prazer responder. =)
E não deixe de continuar seguindo nosso blog e de nos acompanhar também no YouTube.
Até um próximo post!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.
