Para fixarmos de uma vez a teoria que aprendemos sobre peças tracionadas vamos resolver três exercícios de peças laminadas tracionadas. Você pode conferir abaixo o resumo dos exemplo resolvidos:
- uma chapa plana com ligação parafusada e furação enviesada, de modo que será necessário verificar mais de um percurso dos furos;
- perfil U com ligações parafusadas em que é necessário calcular o fator redutor da área efetiva;
- chapa plana com soldas longitudinais.
Para facilitar a apresentação dos problemas a seguir, sempre furos com 22 mm de diâmetro e que todas as peças tracionadas são de aço ASTM A36. Este aço possui a tensão de escoamento de 250 MPa e uma tensão última de 400 MPa.
Caso você prefira, pode conferir também por vídeo as resoluções das questões abaixo:
Chapas planas com ligação parafusada
No primeiro exemplo, estamos atrás da espessura mínima de duas chapas de aço conectadas por parafusos e submetidas a uma esforço de tração de 200 kN. Cada chapa tem 260 mm de largura com furos espaçados verticalmente em 65 mm e horizontalmente em 50 mm..
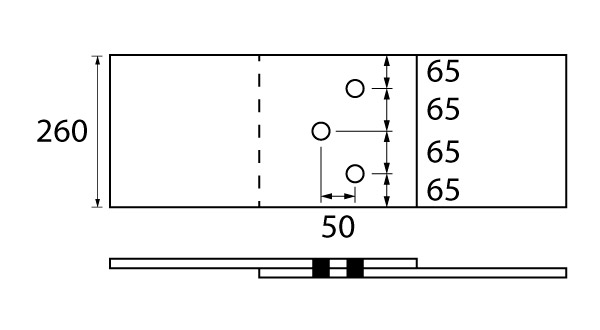
Escoamento da seção bruta
O cálculo da área bruta é feito basicamente pelo produto da largura da chapa pela espessura da mesma. Nós já conhecemos a formulação para verificação do escoamento da seção bruta:
\mathrm{R_{dt} = \dfrac{A_g \cdot f_y}{\gamma_{a1}}}
Como procuramos \mathrm{R_{dt} \geq N}, a área bruta deverá ser:
\mathrm{A_g \geq \dfrac{N \cdot 1,10}{f_y}}
\mathrm{A_g \geq \dfrac{200 \cdot 1,10}{25} = 8,8 \; cm^2}
Ruptura da seção líquida
Na verificação da ruptura da seção líquida, como temos uma furação enviesada, será necessário considerar os dois percursos possíveis através dos furos. Para o primeiro percurso, passaremos através de dois furos apenas:
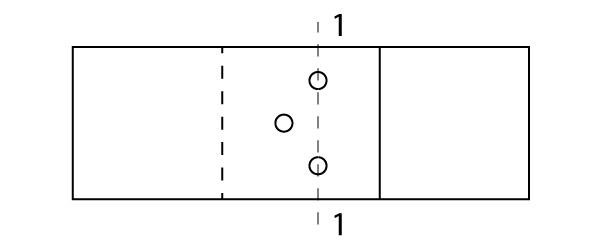
A área líquida do primeiro percurso será:
\mathrm{A_n = \left( 26 - 2 \cdot 2,2 \right) \cdot t = 21,6 \cdot t}
Na segunda situação consideraremos o percurso passando pelos três furos, ou seja, também pelo parafuso intermediário:
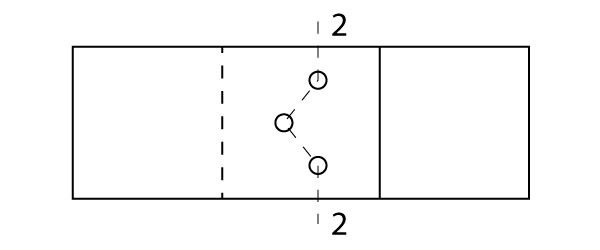
Vamos calcular agora a área líquida para o segundo percurso:
\mathrm{A_n = \left( b - 3 \cdot d_f + 2 \cdot \dfrac{s^2}{4 \cdot g} \right ) \cdot t }
\mathrm{A_n = \left( 26 - 3 \cdot 2,2 + 2 \cdot \dfrac{5^2}{4 \cdot 6,5} \right ) \cdot t = 21,32 \cdot t }
Podemos verificar agora a área líquida necessária para o esforço solicitante:
\mathrm{A_n \geq \dfrac{N \cdot 1,35}{f_u}}
\mathrm{A_n \geq \dfrac{200 \cdot 1,35}{40} = 6,75 \; cm^2}
Agora podemos comparar os valores da espessura para cada situação. Primeiramente, calculando a espessura para seção bruta:
\mathrm{A_g = 26 \cdot t \geq 8,8 \; cm^2}
\mathrm{t \geq 3,38 \; mm}
Considerando agora a área líquida, teremos para o percurso com menor área líquida a seguinte espessura:
\mathrm{A_n = 21,32 \cdot t \geq 6,75 \; cm^2}
\mathrm{t \geq 3,17 \; mm}
O resultado então será o maior dos dois valores, que vale 3,38 mm.
Perfil U com ligação parafusada
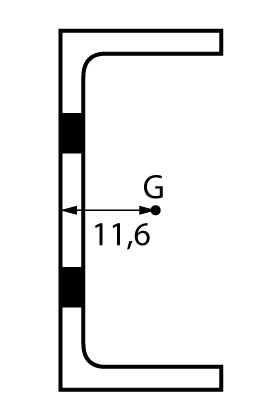
Para o segundo exemplo, consideraremos um perfil U 102 x 8,0 com uma ligação de extremidade de duas linhas com dois parafusos em cada linha, conforme ilustra a figura abaixo.
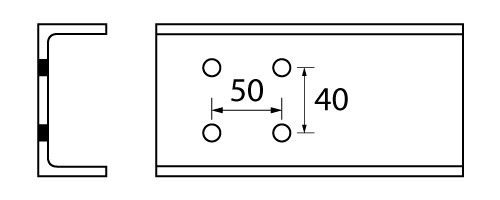
O objetivo do exercício é calcular o esforço de tração resistente pelo perfil. Nesse problema, não verificaremos o cisalhamento do bloco, que é outra forma de ruptura para situações como esta.
Escoamento da seção bruta de peças tracionadas
A fim de calcularmos a normal máxima para o escoamento da seção bruta vamos obter inicialmente a área de aço bruta através de alguma tabela comercial. Para o perfil U 102 x 8,0 a área bruta vale 10,1 cm².
Dessa forma, o esforço cortante resistente vale:
\mathrm{R_{dt} = \dfrac{A_g \cdot f_y}{\gamma_{a1}}}
\mathrm{R_{dt} = \dfrac{10,1 \cdot 25}{\gamma_{1,1}} = 229,6 \; kN}
Ruptura da seção líquida
Inicialmente vamos calcular a área líquida da seção. A mesma será basicamente a área bruta retirando a área ocupada pelos dois furos:
\mathrm{A_{n} = A_g - 2 \cdot d_f \cdot t}
\mathrm{A_{n} = 10,1 - 2 \cdot 2,2 \cdot 0,46 = 8,08 \; cm^2}
A espessura da chapa de 0,46 cm também foi retirada de uma tabela comercial.
Como para essa ligação nem todos os elementos estão conectados, deveremos utilizar um redutor \mathrm{C_t} na área líquida para obter a área efetiva. A redução será dada pela razão entre a distância do plano da ligação até o centro geométrico da seção e o comprimento da ligação.
O comprimento da ligação equivale a distância do primeiro para o último parafuso e vale 5 cm e a distância do plano da ligação até o centro geométrico vale 1,16 cm e também foi retirado da tabela comercial.
\mathrm{C_t = 1 - \dfrac{e_c}{l} \geq 0,60}
\mathrm{C_t = 1 - \dfrac{11,6}{50} = 0,77}
Podemos finalmente calcular a área de aço efetiva:
\mathrm{A_{ef} = A_n \cdot C_t}
\mathrm{A_{ef} = 8,08 \cdot 0,77 = 6,22 \; cm^2}
E agora verificando a tração limite para a ruptura da seção efetiva:
\mathrm{R_{dt} = \dfrac{A_{ef} \cdot f_u}{\gamma_{a2}}}
\mathrm{R_{dt} = \dfrac{6,22 \cdot 40}{1,35} = 184,3 \; kN}
Assim sendo, a tração limitante para esse perfil U será de 184,3 kN, que é o menor dos dois valores.
Chapa plana com solda longitudinal
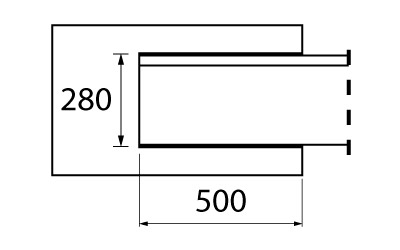
O terceiro e último exemplo que iremos resolver aqui é de uma chapa plana com solda com o comprimento de 50 cm em ambas as bordas. A largura da chapa é de 28 cm e a espessura de 0,4 cm.
Dadas essas informações estamos atrás da tração resistente para a situação.
Escoamento da seção bruta
Vamos calcular inicialmente a área bruta da seção transversal:
\mathrm{A_{g} = 28 \cdot 0,4 = 11,2 \; cm^2}
Agora sim vamos calcular a tração resistente para a seção bruta:
\mathrm{R_{dt} = \dfrac{A_g \cdot f_y}{\gamma_{a1}}}
\mathrm{R_{dt} = \dfrac{11,2 \cdot 25}{\gamma_{1,1}} = 254,5 \; kN}
Ruptura da seção efetiva de peças tracionadas
A área líquida será igual a área bruta da seção, que no caso vale 11,2 cm². Para chegarmos na área efetiva é necessário reduzirmos a área líquida pelo fator \mathrm{C_t}.
O fator de redução irá variar de acordo com a relação entre o comprimento da solda e a largura da chapa:
\mathrm{\dfrac{l_w}{b} = \dfrac{500}{280} = 1,79}
Teremos \mathrm{C_t = 0,87} para o nosso caso, uma vez que o valor de \mathrm{l_w = 1,79 \cdot b} está entre \mathrm{1,5 \cdot b} e \mathrm{2,0 \cdot b}.
Podemos então calcular o esforço de tração resistente para a ruptura da seção efetiva:
\mathrm{R_{dt} = \dfrac{A_{ef} \cdot f_u}{\gamma_{a2}}}
\mathrm{R_{dt} = \dfrac{0,87 \cdot 11,2 \cdot 40}{1,35} = 288,7 \; kN}
Recado final
Com esse post você consolidou mais ainda o que aprendeu sobre peças tracionadas no caso de perfis laminados. Esse assunto é o início para uma quantidade enorme de conteúdo sobre dimensionamento de estruturas metálicas.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
