Eu sei que é difícil começar os estudos na área de estruturas metálicas. O interessante é que focando em cada solicitação separadamente, podemos aprender um pouco mais a cada dia.
Aqui você encontrará como dimensionar peças metálicas submetidas à tração de acordo com a norma ABNT/NBR: 8800 (2008).
Introdução
As peças tracionadas são aquelas que estão sujeitas unicamente à esforços de tração, ou seja, a tração encontra-se centrada na peça. Alguns exemplos de peças tracionadas são tirantes, contraventamentos, treliças (nos banzos, montantes e diagonais) etc.
Os perfis mais usuais para peças tracionadas são barras redondas, barras chatas, perfis laminados simples (como cantoneiras) e também a composição de dois perfis laminados, conforme apresentado na figura abaixo.
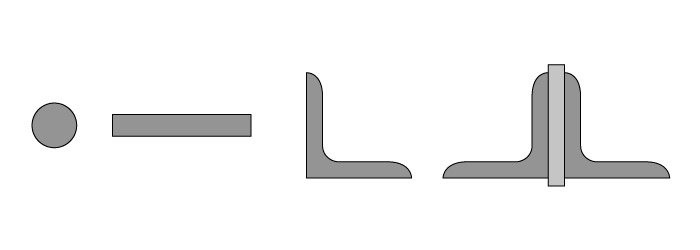
Vale destacar que esses perfis apresentados acima são apenas os mais comuns, dependendo da situação, outros podem ser empregados.
Dimensionamento
Em uma peça sujeita a tração axial, devemos verificar a resistência a partir de duas situações: ruptura da seção com furos e escoamento da seção bruta, o que ocasiona grandes deformações.
Escoamento da seção bruta
A força limite para verificação do escoamento da área bruta pode ser calculada pela formulação abaixo. É simplesmente o produto da área bruta pela tensão de escoamento do aço, minorada pelo coeficiente \mathrm{\gamma_{a1}} presenta na norma ABNT/NBR: 8800 (2008).
\mathrm{R_{dt} = \dfrac{A_g \cdot f_y}{\gamma_{a1}}}
No caso de combinações de ações normais, \mathrm{\gamma_{a1} = 1,10}.
Ruptura da seção com furos (área líquida efetiva)
No caso da seção com furos, também denominada de seção líquida efetiva, utilizaremos agora a tensão resistente à tração e o coeficiente \mathrm{\gamma_{a1}}.
\mathrm{R_{dt} = \dfrac{A_{ef} \cdot f_u}{\gamma_{a2}}}
No caso de combinações de ações normais, \mathrm{\gamma_{a2} = 1,35}.
Cálculo da área líquida
Inicialmente, é importante aprendermos a obter a dimensão dos furos.
Para isso, podemos considerar, em linhas gerais, um adicional de 3,5 mm no diâmetro do parafuso. Desse valor, 1,5 mm equivalem apenas a uma folga entre furo e parafuso e 2 mm prevem um dano no material na borda do furo devido ao puncionamento.
\mathrm{d_{f} = d_{p} + 3,5\; mm}
Conhecendo a dimensão dos furos, vamos avançar para o cálculo da seção transversal líquida em si. Para isso, devemos analisar os possíveis percursos de ruptura de acordo com a furação realizada, a fim de obter o menor valor de área líquida.
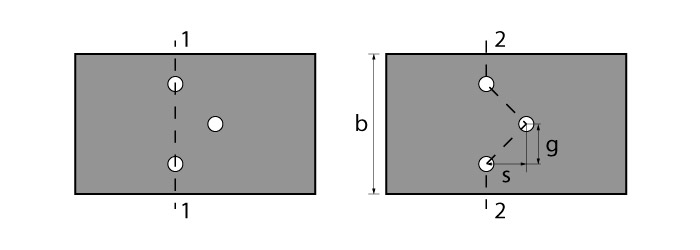
Na figura ilustrada acima, temos o caminho 1-1 em que a área líquida será:
\mathrm{A_n = \left( b - 2 \cdot d_f \right) \cdot t }
Para o percurso 2-2, teremos a seguinte área líquida:
\mathrm{A_n = \left( b - 3 \cdot d_f + 2 \cdot \dfrac{s^2}{4 \cdot g} \right ) \cdot t }
Observe que para esse percurso temos dois trechos inclinados em que o deslocamento horizontal é \mathrm{s} e o deslocamento vertical é \mathrm{g} e atravessamos três furos. Para cada trecho inclinado, adicionamos a parcela \mathrm{\dfrac{s^2}{4 \cdot g}}.
Cálculo da área líquida efetiva
No caso em que nem todos os segmentos estão conectados, ocorre uma concentração de tensões nos segmentos ligados. Isso é considerado nos cálculos através de um coeficiente de redução da área líquida. Nesse caso, a área líquida é calculada pela equação apresentada abaixo:
\mathrm{A_{ef} = C_t \cdot A_n}
A seguir, vou apresentar um conjunto de situações diferentes para o cálculo do coeficiente de redução.
Tração transmitida diretamente para cada elemento
No caso em que a força de tração é transmitia diretamente para cada um dos elementos da seção transversal, não é necessário reduzir a área líquida. Desse modo, tomamos \mathrm{C_t = 1,00}.
Transmissão da tração por soldas transversais
No caso de ligações soltadas feitas com soldas transversais, o coeficiente de redução será a relação entre a área soldada e a área bruta da seção:
\mathrm{C_t = \dfrac{A_{contato}}{A_g}}
Chapas planas com soldas longitudinais
No caso de chapas planas com soldas longitudinais ao longo de ambas as suas bordas, o coeficiente será dado pela relação da largura da chapa e do comprimento da solda:
\mathrm{C_t = 1,00} para \mathrm{l_w \geq 2 \cdot b};
\mathrm{C_t = 0,87} para \mathrm{1,5 \cdot b \leq l_w < 2 \cdot b};
\mathrm{C_t = 0,75} para \mathrm{b \leq l_w < 1,5 \cdot b}.
A figura abaixo ilustra os casos de soldas transversais e longitudinais apresentados acima.
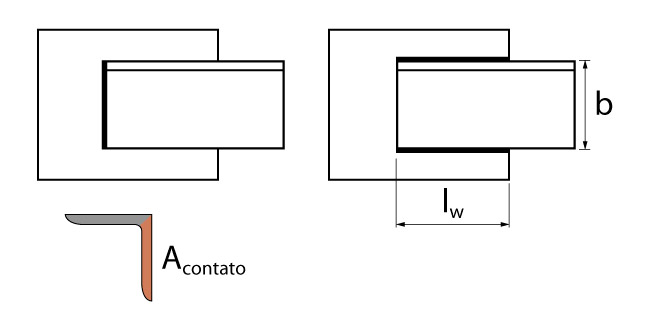
Seções transversais abertas
Nos perfis de seção aberta, podemos calcular o \mathrm{C_t}:
\mathrm{C_t = 1 - \dfrac{e_c}{l} \geq 0,60}
O valor de \mathrm{e_c} equivale a distância entre o plano da ligação até o centro geométrico da seção que resiste ao esforço e o valor de \mathrm{l} é o comprimento da ligação, sendo o comprimento da cordão de solda para ligações soldadas e a distância do primeiro ao último parafuso para ligações parafusadas.
O limite superior para o coeficiente de redução vale 0,9 e não são permitidas ligações que resultem em um coeficiente inferior a 0,6.
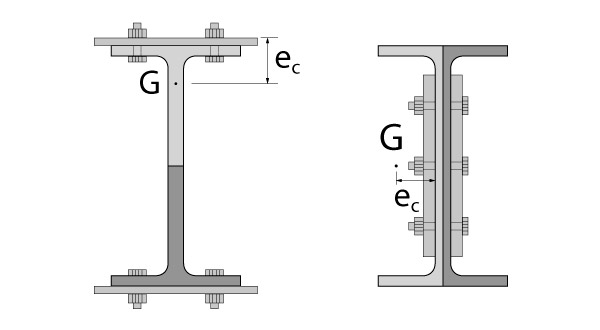
A figura abaixo apresenta conexões onde só há um plano de ligação. Dessa forma, a excentricidade é a distância do plano até o centro de gravidade da seção inteira.
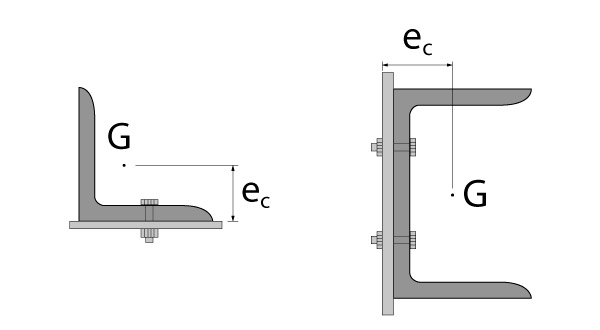
No caso de seções com um eixo de simetria, é necessário também a existência de simetria nas ligações. Conforme ilustra a figura abaixo, o centro de gravidade para o cálculo de \mathrm{e_c} será relativo apenas a meia seção.
Limites de esbeltez
Diferente os elementos comprimidos, as peças tracionadas podem estar submetidas a elevados índices de liquidez. Isso pode ocasionar vibrações excessivas, o que constitui um Estado Limite de Serviço. Segundo a ABNT/NBR: 8800 (2008), a esbeltez dos elementos tracionados não deve ser superior a 300.
Vale lembrar que o índice de esbeltez é calculado pela razão entre o comprimento do elemento e raio de giração:
\mathrm{\lambda = \dfrac{l}{r}}
No caso de tirantes formados por barras redondas em pré-tensionadas ou montadas com pré-tensão, podemos exceder esse valor de 300.
Recado final
Nesse ponto você já conferiu a teoria sobre dimensionamento de peças metálicas submetidas à esforços de tração. Para fecharmos esse conteúdo irei escrever também um post apenas com exemplos aplicados.
Fonte:
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8800: Projeto de estruturas de aço e de estruturas mista de aço e concreto de edifícios. Rio de Janeiro, 2008.
CHAMBERLAIN, Z.; FICANHA, R.; FABEANE, R. Projeto e Cálculo de Estruturas de Aço: Edifício Industrial Detalhado. Rio de Janeiro: Elsevier, 2013.
PFEIL, W; PFEIL, M. Estruturas de Aço: Dimensionamento Prático. Rio de Janeiro: LTC, 2013.
SOUZA, A. Dimensionamento de elementos e ligações em estrutura de aço. São Carlos, EdUFSCar, 2017.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Melhor assunto!