Eu sei que você já deve estar cheio dos nossos posts sobre canais e e sobre a fórmula de Manning.
Porém, me senti no dever de reservar um post somente sobre canais circulares, pois são os que, de maneira geral, os estudantes sentem mais dificuldades.
Então, nesse post iremos resolver duas questões de canais circulares.
Tenho certeza que ao final do post, você terá domínio sobre o assunto e não terá mais dúvidas relativas a isso!
Agora, vamos às questões.
Exemplo 1
Considere o canal circular com a seção transversal ilustrada na figura abaixo.
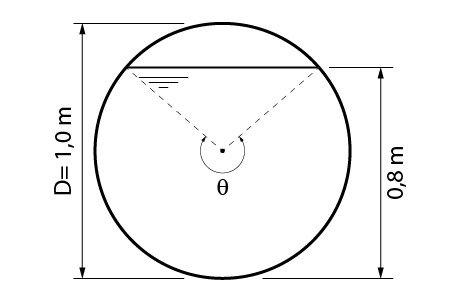
Considerando que a declividade de fundo do canal seja de 0,0001 m/m e que o mesmo seja de concreto, qual a vazão transportada por esse canal?
Resolução 1
Bem, antes de iniciarmos a resolução desse exercício, sugiro fortemente que você leia o nosso post com a teoria sobre canais circulares, já que aqui vou apresentar formulações que foram deduzidas em tal post!
Mas, se você quer dar uma rápida revisada, sem precisar ler o post anterior, preparei um vídeo com a revisão dessa teoria e com a resolução dessa questão, assiste abaixo!
Agora iniciando, de fato, a resolução, vamos lembrar de algumas formulações importantes.
A primeira dela é a fórmula de Manning:
\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}
Onde:
- Q: vazão de escoamento;
- n: coeficiente de rugosidade do canal;
- \mathrm{I_0}: inclinação longitudinal do canal;
- A: área molhada da seção transversal;
- \mathrm{R_h}: raio hidráulico da seção.
A fórmula de Manning será usada para o cálculo da vazão no canal.
Entretanto, precisamos saber como calcular a área molhada e o raio hidráulico, que já deduzimos, como:
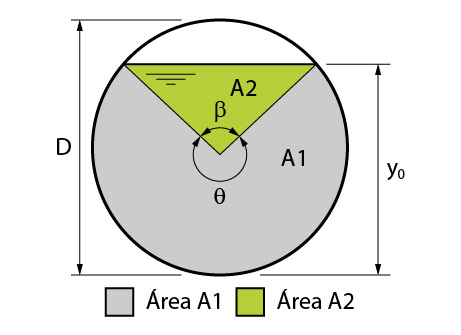
\mathrm{A=D^2\dfrac{\theta-sen\theta}{8}}
\mathrm{R_h=\dfrac{D\cdot(1-sen\theta/\theta)}{4}}
Agora que já relembramos as principais formulações, vamos calcular cada um dos elementos geométricos.
Cálculo da área molhada e raio hidráulico
Você deve ter percebido pelas formulações apresentadas que ambas são dependentes do ângulo central \mathrm{\theta}.
Então, o primeiro passo para o cálculo dos elementos geométricos é calcularmos esse ângulo central.
Vamos olhar para o canal sob a seguinte perspectiva.
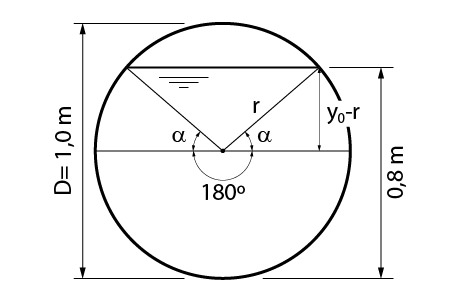
Você concorda que \mathrm{\theta=180^o+2\cdot\alpha}?
Então, se determinarmos \mathrm{\alpha}, automaticamente saberemos o valor de \mathrm{\theta}.
Podemos dizer que:
\mathrm{sen\alpha=h/r}
\mathrm{sen\alpha=0,3/0,5}
\mathrm{\alpha=36,87^o}
Logo:
\mathrm{\theta=180^o+2\cdot 36,87^o}
\mathrm{\theta=253,74^o}
De posse do ângulo central, já podemos calcular a área molhada do nosso canal.
\mathrm{A=D^2\dfrac{\theta-sen\theta}{8}}
\mathrm{A=1^2\dfrac{4,43-(-0,96)}{8}}
\mathrm{A=0,674 m^2}
Pronto! Agora vamos calcular o raio hidráulico, também pela fórmula apresentada.
\mathrm{R_h=\dfrac{D\cdot(1-sen\theta/\theta)}{4}}
\mathrm{R_h=\dfrac{1\cdot(1-sen\theta/\theta)}{4}}
\mathrm{R_h=0,304 m}
Agora já podemos calcular a vazão transportada no canal.

Está pronto para elevar suas habilidades em instalações pluviais? Aprenda com profissionais experientes e obtenha certificação reconhecida. Clique no banner e veja como nosso curso pode transformar sua carreira.
Cálculo da vazão
Para calcularmos a vazão, basta utilizarmos a fórmula de Manning.
Como já temos a área molhada, o raio hidráulico e a declividade de fundo do canal, precisamos apenas saber qual o coeficiente de rugosidade n iremos utilizar. Para isso, vamos olhar a seguinte tabela.
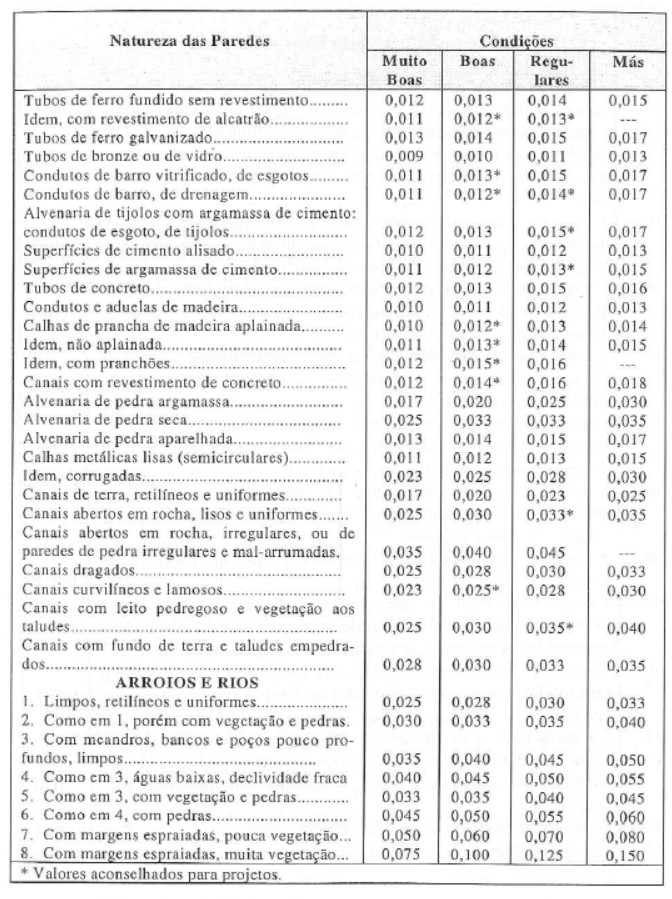
Por essa tabela, sabendo que nosso canal é de concreto, poderíamos usar um valor de n entre 0,012 e 0,016. Porém, vamos utilizar o valor aconselhado de projeto que é n=0,013.
Então, utilizando a fórmula de Manning, temos:
\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}
\mathrm{\dfrac{0,013\cdot Q}{\sqrt{0,0001}}=A\cdot R_{h}^{2/3}}
\mathrm{Q=0,234 m^3/s}
Prontinho! Determinamos que a vazão transportada por esse canal é de 0,234 m³/s.
Agora vamos ver a resolução do mesmo problema com a utilização de tabelas.
Resolução 2
Como já vimos no nosso post com a teoria sobre canais circulares, podemos resolver esse problema com a utilização de tabela, a partir da seguinte formulação.
\mathrm{D=\dfrac{M}{K_1}}
Onde:
\mathrm{M=\left(\dfrac{n\cdot Q}{\sqrt{I_o}}\right)^{3/8}}
E \mathrm{{K_1}} pode ser obtido através da tabela abaixo.
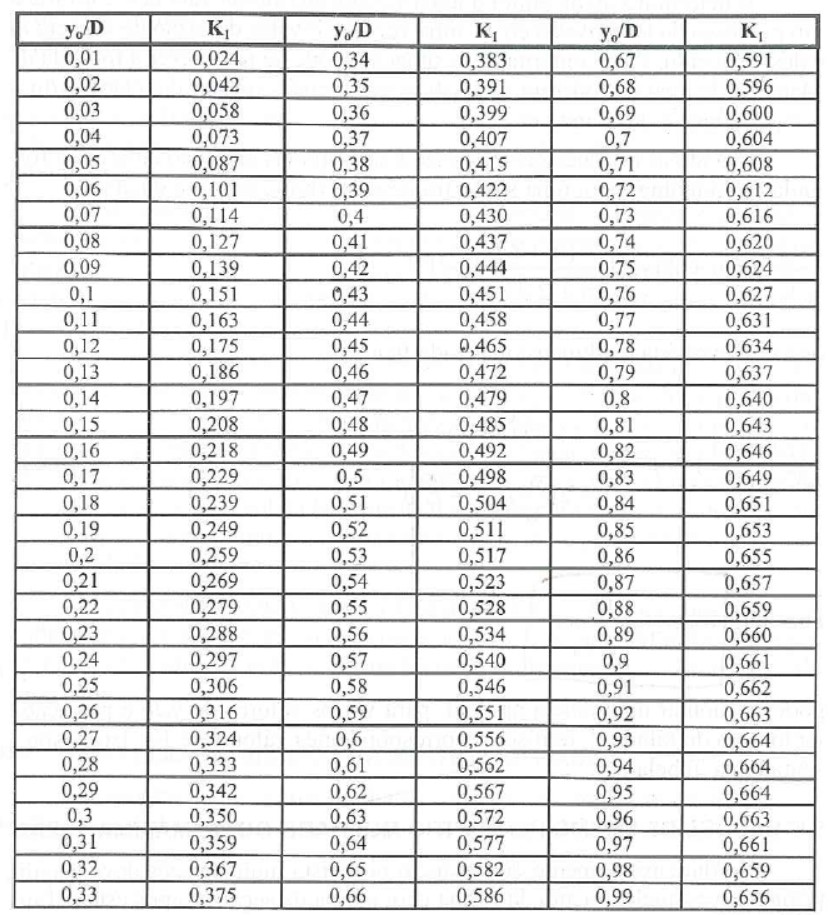
Como temos que \mathrm{y_o/D=0,8}, logo, \mathrm{{K_1=0,64}}.
Então, utilizando a formulação, temos que:
\mathrm{M=\left(\dfrac{n\cdot Q}{\sqrt{I_0}}\right)^{3/8}}
\mathrm{M=\left(\dfrac{0,013\cdot Q}{\sqrt{0,0001}}\right)^{3/8}}
\mathrm{M=\left(1,3\cdot Q\right)^{3/8}}
Logo:
\mathrm{D=\dfrac{M}{K_1}}
\mathrm{1=\dfrac{\left(1,3\cdot Q\right)^{3/8}}{0,64}}
\mathrm{Q=0,234 m^3/s}
Viu como para canais circulares é mais simples utilizar a tabela e chegar ao mesmo resultado?
Agora, vamos para um exercício de canal com seção semicircular
Exemplo 2
O exemplo aplicado agora será de uma calha de instalações de águas pluviais de formato semicircular.
Consideremos então, a calha abaixo.
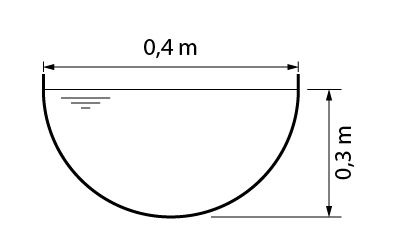
Sabendo que a inclinação longitudinal da calha é de 1% e que a norma recomenda que seja utilizado um coeficiente de rugosidade n=0,011, qual a vazão transportada por tal canal?
Resolução com tabela
Para essa resolução, vamos direto para o uso da tabela!
Para esse caso, temos que \mathrm{y_o/D=0,50}.
Logo, \mathrm{K_1=0,498}.
Sabendo disso, podemos calcular M.
\mathrm{M=\left(\dfrac{n\cdot Q}{\sqrt{I_0}}\right)^{3/8}}
\mathrm{M=\left(\dfrac{0,011\cdot Q}{\sqrt{0,01}}\right)^{3/8}}
\mathrm{M=\left(0,11\cdot Q\right)^{3/8}}
Agora, basta utilizarmos a fórmula já apresentada anteriormente.
\mathrm{D=\dfrac{M}{K_1}}
\mathrm{0,400=\dfrac{\left(0,11\cdot Q\right)^{3/8}}{0,498}}
\mathrm{Q=0,123 m^3/s}
Pronto! Já determinamos o valor da vazão transportada para esse canal por meio da tabela.
Agora, vamos resolver o mesmo exemplo com utilização da nossa planilha de águas pluviais.
Resolução com planilha
Como comentei no enunciado da questão, tal exemplo é muito usual em instalações de águas pluviais.
Então, podemos utilizar nossa planilha de dimensionamento dos elementos de instalações de águas pluviais!
Como dados de entrada nós temos:
- Tipo de calha: semicircular;
- Diâmetro: 400 mm;
- Lâmina d’água: 200 mm;
- Inclinação: 1%;
- n: 0,011.
Como dado de saída, a planilha nos retorna a capacidade de vazão da nossa calha, porém em l/min, conforme figura abaixo.

Tenho certeza que após a leitura desse post você já está se sentindo muito mais seguro sobre a utilização da fórmula de Manning e sobre o cálculo de canais circulares!
Mas se ficou alguma dúvida, deixa nos comentários que vai ser um prazer te responder!
E não deixe de continuar seguindo nosso blog e de nos acompanhar também no YouTube.
Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

Eu acredito que o valor da relação y/D seja 0,75
Oi,
O que significa h=0,3?