Tenho certeza que você já leu nosso post sobre a fórmula de Manning em condutos retangulares.
Mas ao final do post deve ter se perguntado: e como faço para calcular canais trapezoidais e circulares?
Calma. Te prometo que ao final desse post você saberá como calcular canais com essas geometrias!
Então, sem mais delongas, vamos ao conteúdo.
Fórmula de Manning
Inicialmente, temos que relembrar a fórmula de Manning, que é a mais usual para o cálculo de escoamentos em condutos livres, que é o caso de canais.
Segue a formulação:
\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}
Onde:
- Q: vazão de escoamento;
- n: coeficiente de rugosidade do canal;
- \mathrm{I_0}: inclinação longitudinal do canal;
- A: área molhada da seção transversal;
- \mathrm{R_h}: raio hidráulico da seção.
Pronto, relembrando dessa formulação e dos conceitos de área molhada e raio hidráulico, resolveremos tranquilamente problemas tanto para seções trapezoidais como para seções circulares.
Então, agora vamos revisar esses conceitos rapidamente!
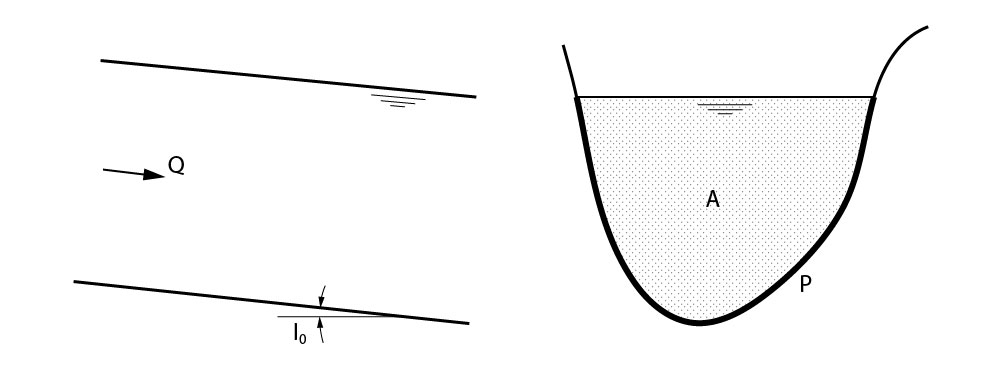
- Área molhada (A): essa é toda a área da seção reta do escoamento.
- Perímetro molhado (P): é o perímetro de contato entre o conduto e o líquido, considerando fundo e paredes.
- Raio Hidráulico (Rh): é razão entre a área molhada e o perímetro molhado. Matematicamente, a fórmula do raio hidráulico é:
\mathrm{R_h=\cdot{P}{A}}
Então, agora que você já relembrou tais conceitos, vamos começar a estudar os canais de seção trapezoidal.
Canais de seção trapezoidal
Para ilustrar melhor esse caso, achei mais conveniente resolvermos um exemplo prático.
Portanto, considere a seguinte seção transversal de um canal.
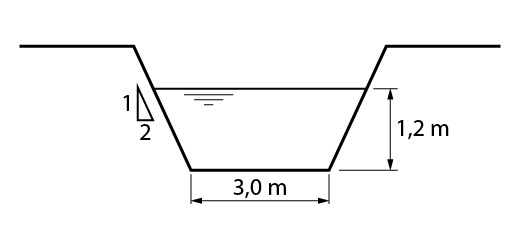
Sabendo que a inclinação longitudinal é de 0,2% e que podemos considerar o coeficiente de rugosidade das paredes como n=0,013, qual é a vazão para a situação apresentada?
Resolução
Então, como já falamos no post anterior, a resolução é bem simples. Precisamos inicialmente calcular os elementos geométricos de escoamento.
Vamos começar pela área molhada!
Cálculo da área molhada
O cálculo da área molhada é basicamente a área de um trapézio.
Entretanto, sabemos apenas a base menor (fundo do canal) e altura da lâmina d’água.
Como sabemos também a inclinação dos taludes laterais do canal, podemos calcular a largura B, apresentada na figura abaixo.
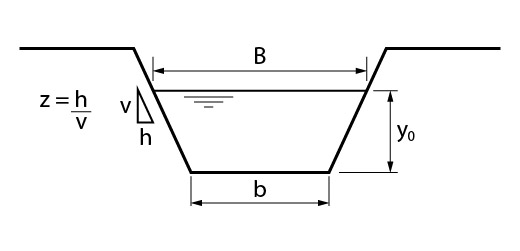
\mathrm{B=b+2\cdot Z\cdot y_o}
Onde:
- Z: inclinação do talude lateral do canal.
- \mathrm{y_o}: altura da lâmina d’água.
Então, realizando esse cálculo, chegamos ao valor de B:
\mathrm{B=3+2\cdot 2\cdot 1,2}
\mathrm{B=7,8m}
De posse de B, podemos então calcular a área molhada, que é a área do trapézio da seção transversal:
\mathrm{A=\dfrac{(b+B)\cdot y_o}{2}}
\mathrm{A=\dfrac{(3+7,8)\cdot 1,2}{2}}
\mathrm{A=6,48 m^2}
Pronto! Já determinamos a área molhada, agora vamos determinar o raio hidráulico da seção.
Cálculo do raio hidráulico
Para o cálculo do raio hidráulico, precisamos inicialmente determinar o perímetro molhado da seção.
O perímetro molhado é composto pela soma dos comprimentos do fundo do canal e das paredes que estão em contato com o líquido.
O fundo já sabemos que é b=3,0 m. Logo, basta determinarmos o comprimento das paredes em contato com o líquido para encontrarmos o perímetro do molhado do canal.
Então, vamos analisar a seguinte figura, que representa a região do talude do nosso canal.
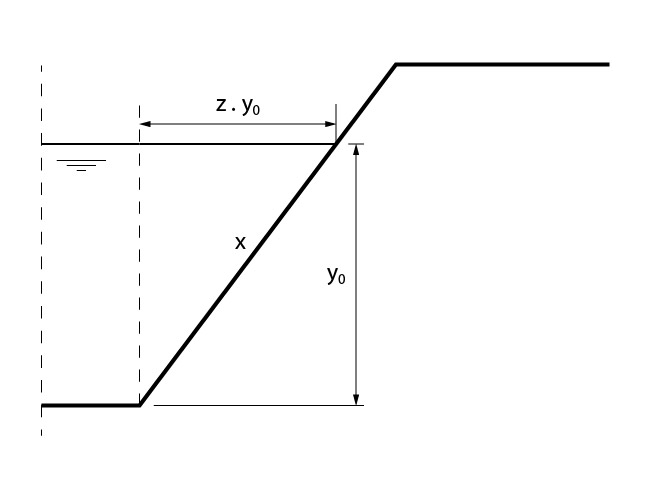
Perceba que podemos encontrar o valor do comprimento x simplesmente pelo teorema de Pitágoras.
\mathrm{x^2=y_{0}^{2}+(Z\cdot y_0)^2}
\mathrm{x^2=1,2^{2}+(2\cdot 1,2)^2}
\mathrm{x=2,68m}
Logo, temos que nosso perímetro será:
\mathrm{P=b+2x=3+2\cdot 2,68}
\mathrm{P=8,36m}
Como sabemos que a fórmula do raio hidráulico é a razão entre a área molhada e o perímetro molhado, temos:
\mathrm{R_h=\dfrac{6,48}{8,36}}
\mathrm{R_h=0,775m}
Prontinho! Viu como foi bem fácil determinar a área molhada e calcular o raio hidráulico?

Está pronto para elevar suas habilidades em instalações pluviais? Aprenda com profissionais experientes e obtenha certificação reconhecida. Clique no banner e veja como nosso curso pode transformar sua carreira.
Como as demais características de escoamento já foram dados na questão, podemos agora utilizar a fórmula de Manning.
Cálculo da vazão
Como já falamos anteriormente, para determinarmos a vazão de um conduto livre, como é o caso de um canal, ou de uma calha de águas pluviais, devemos utilizar a fórmula de Manning.
\mathrm{\dfrac{n\cdot Q}{\sqrt{I_0}}=A\cdot R_{h}^{2/3}}
\mathrm{\dfrac{0,013\cdot Q}{\sqrt{0,002}}=6,48\cdot 0,775^{2/3}}
\mathrm{Q=18,81m^3/s}
Portanto, determinamos assim a vazão no nosso canal trapezoidal!
Vale ressaltar que em algumas literaturas, como por exemplo no livro Hidráulica Básica, do Prof. Porto, você pode encontrar tabelas para o cálculo de canais trapezoidais.
Tais tabelas relacionam a altura de lâmina d’água e inclinação do talude para chegar em valores de constantes, para, a partir delas, determinarmos a vazão do canal.
Entretanto, essas tabelas apenas sistematizam o que acabamos de fazer.
Por isso, julgo que seja mais interessante você entender como calculamos aqui, que você não terá nenhuma dificuldade em calcular outros canais trapezoidais!
Então, agora vamos ver um pouco sobre canais circulares.
Canais de seção circular
Para esse tipo de canal, vamos realizar o mesmo procedimento realizado no exemplo anterior.
Porém, para seções circulares, a análise de área molhada e raio hidráulico é um pouco mais complexa.
Logo, acho mais interessante começarmos com um exemplo não numérico, para deduzirmos as fórmulas e só depois disso resolvermos uma questão.
Então, considere esse seguinte canal circular da figura abaixo.
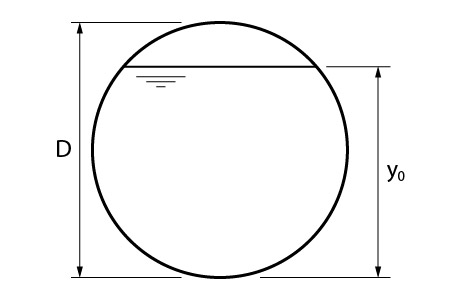
Vamos agora analisar geometricamente essa seção.
Cálculo da área molhada
Antes de iniciarmos, vamos ver o mesmo canal já apresentado de uma outra forma!
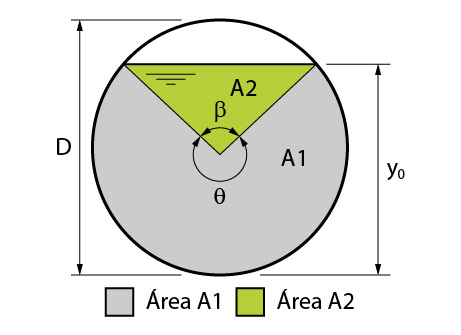
Para facilitar nosso cálculo, perceba acrescentamos um ângulo central \mathrm{\theta}.
Perceba também que dividimos a área molhada em duas áreas distintas. Vamos então, começar calculando A1.
Para isso, vamos fazer uma regra de três simples, lembrando que para a área total do círculo vale \mathrm{\dfrac{\pi\cdot D^2}{4}} e que o ângulo central para esse caso seria de \mathrm{2\pi}. Logo:
\mathrm{\dfrac{ \pi\cdot D^2}{2\cdot \pi \cdot 4}=\dfrac{A_1}{\theta}}
\mathrm{A_1=\dfrac{D^2\cdot\theta}{8}}
Então, agora que já sabemos A1, vamos determinar A2.
Você pode perceber que é simplesmente a área de um triângulo, logo pode ser determinado como:
\mathrm{A_2=\dfrac{r\cdot r\cdot sen\beta}{2}}
\mathrm{A_2=\dfrac{D^2\cdot sen\beta}{8}}
\mathrm{A_2=-\dfrac{D^2\cdot sen\theta}{8}}
Ou seja, podemos dizer que a área molhada da seção vale:
\mathrm{A=A_1+A_2}
\mathrm{A=D^2\dfrac{\theta-sen\theta}{8}}
Pronto! Já deduzimos uma fórmula geral para determinarmos a área molhada a partir do diâmetro do conduto e do ângulo central \mathrm{\theta}.
A seguir vamos calcular o raio hidráulico da seção.
Cálculo do raio hidráulico
Como você já sabe, para calcularmos o raio hidráulico, precisamos antes determinar o perímetro molhado do canal.
Para esse caso, basta fazermos uma regra de três, lembrando que para o ângulo central de \mathrm{2\cdot\pi} temos que o perímetro da circunferência é de \mathrm{D\cdot\pi}. Logo:
\mathrm{\dfrac{D\cdot\pi}{2\cdot\pi}=\dfrac{P}{\theta}}
\mathrm{P=\dfrac{D\cdot\theta}{2}}
Pronto! Agora que já sabemos o perímetro molhado, podemos aplicar a fórmula apresentada para o cálculo do raio hidráulico:
\mathrm{R_h=\dfrac{A}{P}}
\mathrm{R_h=\dfrac{D\cdot(1-sen\theta/\theta)}{4}}
Agora que já sabemos como calcular a área molhada e o raio hidráulico da seção, tudo fica mais fácil!
Mas podemos deixar ainda mais fácil!
Cálculo da seção com utilização de tabela
Mas como você percebeu, o cálculo dos elementos geométricos para seções circulares é um pouco mais complexo, logo, para esse caso, eu acredito que seja mais simples a utilização de tabelas.
Como citei anteriormente, a tabela nada mais é do que a aplicação de valores para as fórmulas que já encontramos, mas ela pode facilitar na resolução de exemplos práticos.
Então, para a utilização da tabela, devemos utilizar a seguinte formulação:
\mathrm{D=\dfrac{M}{K_1}}
Onde:
\mathrm{M=\left(\dfrac{n\cdot Q}{\sqrt{I_0}}\right)^{3/8}}
Se você é atento, já percebeu aquilo que havia falado.
A utilização da tabela nada mais é do que a simples aplicação da fórmula de Manning.
Na tabela, que faz uma relação entre a altura da lâmina d’água e o diâmetro do conduto, você encontra \mathrm{{K_1}}.
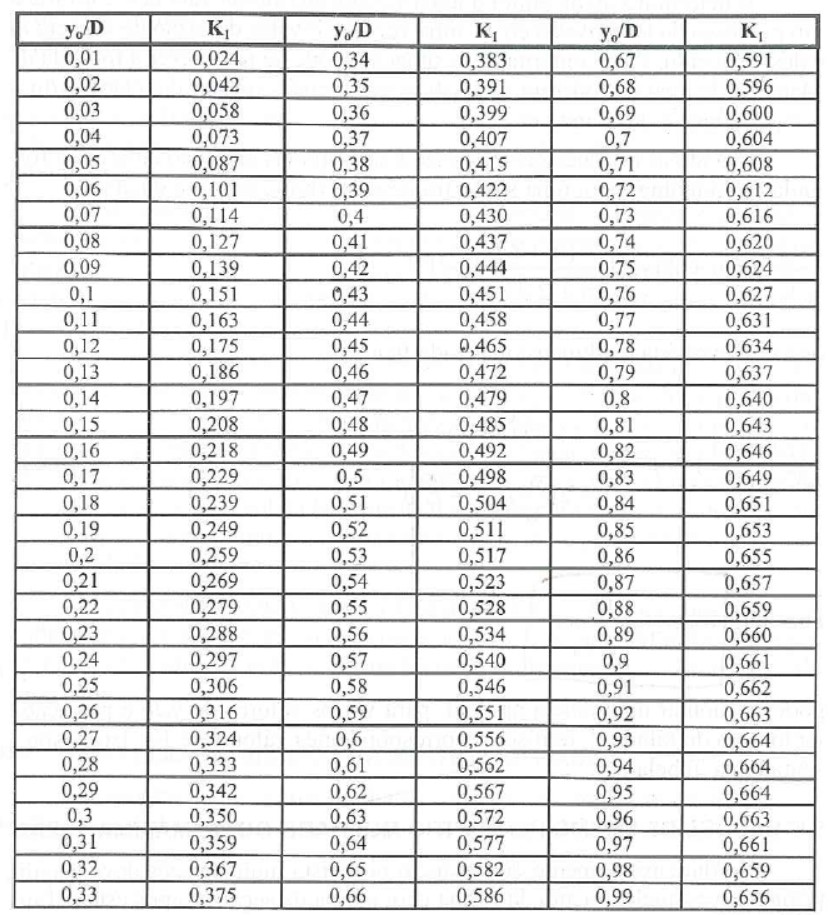
Ufa!
Enfim terminamos hein?!
No próximo post faremos algumas questões com escoamentos em canais circulares, para você fixar de vez esse conteúdo!
Espero que esse post tenha te ajudado, mas caso você ainda tenha alguma dúvida, pode deixar nos comentários que vai ser um prazer responder.
Além disso, se tiver alguma alguma sugestão para posts futuros, comenta aqui embaixo que a gente vai fazer o máximo para poder atender!
Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!
Até a próxima!
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

gostei da postagem, muito boa.
Eu gostaria de ter a parte de calculo do circulo em uma planilha de exel.
Se for possivel eu agradeço.
Bom dia, Luís! Temos nossa planilha de dimensionamento de calhas. Funciona exatamente como expliquei no texto. Abraço!