No post anterior, explicamos quais os procedimentos básicos para realizar uma avaliação em massa para fins fiscais e a elaborar uma Planta Genérica de Valores.
Agora, vamos solidificar o que foi aprendido sobre avaliações em massa até o momento. Para tanto, propomos um exercício hipotético de uma PGV pelo Método Comparativo Direto de Dados de Mercado, através da inferência estatística.
Confira a seguir!
Exemplo prático
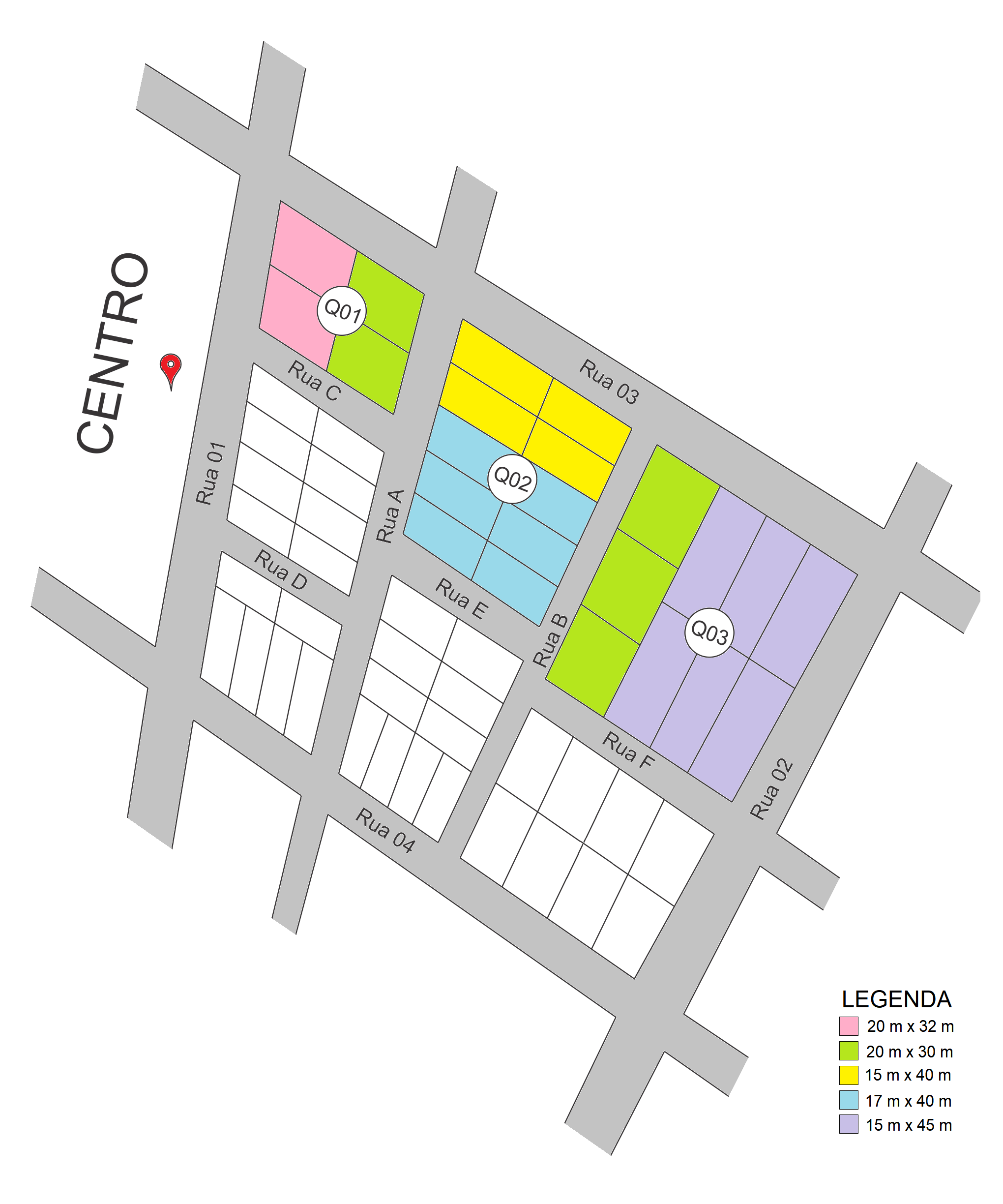
Pretende-se elaborar a Planta Genérica de Valores para os lotes das quadras 01, 02 e 03 do setor da figura abaixo, caracterizado como uma zona residencial popular, a partir de uma amostra dos imóveis da cidade, sabendo que a quadra 01 está distante 100 m do centro da cidade, a quadra 02, 200 m e a quadra 03, 300 m.
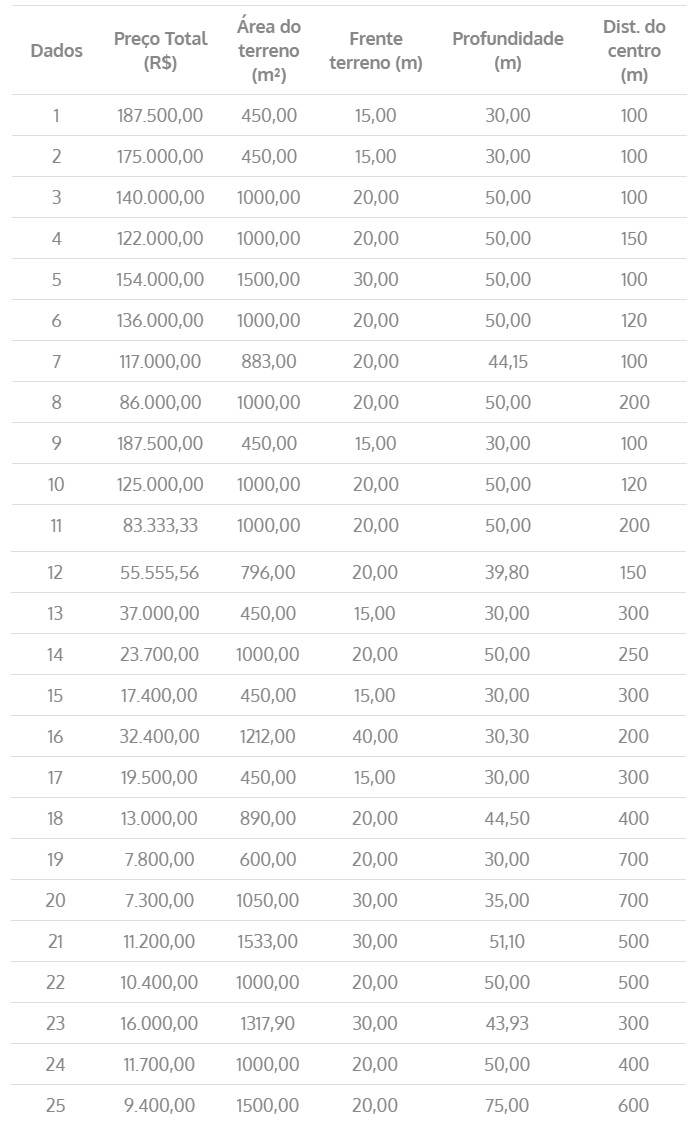
Elementos da amostra do mercado:
RESOLUÇÃO:
Para resolução do nosso exemplo, faremos uso do Método Comparativo Direto por Inferência Estatística, pois fornece um resultado mais preciso, embora também possa ser resolvido com mais facilidade pelo Tratamento por Fatores.
Desse modo, faremos uso do software Microsoft Office Excel para nos ajudar nessa tarefa. Então, caso queira mais informações a respeito das ferramentas e comandos utilizados neste exercício, clique aqui.
Passo 01: Número mínimo de elementos
A partir dos dados fornecidos, podemos inferir que a variável dependente em questão é o preço unitário e que existem três variáveis independentes para este modelo: frente do terreno, profundidade do terreno e distância ao centro. Vale lembrar que a área poderia ser usada como variável, mas não há necessidade, nesta situação, pois já estamos utilizando as variáveis frente e profundidade do terreno.
Desse modo, o número mínimo de dados efetivamente utilizados no modelo (para atingir o grau de fundamentação mínimo) deve obedecer ao seguinte critério:
\mathrm{n=3(k+1)=3(3+1)=12\:elementos}
Como a amostra para esse modelo possui 25 elementos, podemos concluir que o grau de fundamentação mínimo foi atingido e, dessa forma, a amostra pode ser utilizada.
Passo 02: Teste de validação da variável independente
Para nos pouparmos de eventuais erros decorrentes de outliers na nossa amostra, iremos agora identificá-los e corrigí-los, se existir.
Então, para isso, faremos primeiramente o teste de validação das variáveis independentes conhecido como estatística T, que mede o erro da estimativa do parâmetro, ou seja, o erro de cada variável independente para o modelo.
Para esse passo, o valor que devemos coletar é o “valor-P”, presente na tabela ANOVA de Regressão, que é o seguinte:
\mathrm{(valor-P)_{frente}=0,07005389955891=7,00}% < 30% ⇒ OK!
\mathrm{(valor-P)_{profundidade}=0,11313639653546=11,31}% < 30% ⇒ OK!
\mathrm{(valor-P)_{profundidade}=0,000239767126778215=0,00}% < 30% ⇒ OK!
Passo 03: Teste de significância do modelo
O próximo passo da análise dos dados diz respeito ao teste de significância do modelo, que indica quantas vezes o Grau de Liberdade da Regressão é maior do que o Grau de Liberdade dos Resíduos.
Para esse passo, o valor que devemos buscar é o “F de significação”, presente na tabela ANOVA de Regressão, que é o seguinte:
\mathrm{F\:de\: significação=0,0000827975798962847=0,0083}% ≤ 5% ⇒ OK!
Passo 04: Normalidade da amostra
Para essa etapa, faremos uso da tabela de resíduos fornecida pela regressão dos dados, onde reordenaremos a coluna de resíduos padrão na ordem crescente para que seja possível analisarmos a normalidade do modelo.
Tabela 1 – Resíduos padronizados na ordem crescente
| Dados | Resíduos padrão |
| 15 | -1,52254254 |
| 17 | -1,460780347 |
| 12 | -1,172567394 |
| 14 | -0,956978514 |
| 13 | -0,946095409 |
| 18 | -0,524163796 |
| 7 | -0,444097036 |
| 16 | -0,412604225 |
| 11 | -0,412533943 |
| 24 | -0,381431524 |
| 8 | -0,377241262 |
| 23 | -0,366129102 |
| 10 | -0,252746625 |
| 3 | -0,152140499 |
| 4 | -0,14557808 |
| 6 | -0,107164314 |
| 5 | 0,052791591 |
| 22 | 0,090939331 |
| 19 | 0,445584367 |
| 21 | 0,785260239 |
| 20 | 1,229304589 |
| 25 | 1,349458468 |
| 2 | 1,64873061 |
| 1 | 2,016362709 |
| 9 | 2,016362709 |
Conforme a NBR 14.653-2:2011 (anexo A), a verificação da normalidade da amostra pode ser realizada pelo histograma dos resíduos padronizados, que deverá se assemelhar a uma distribuição normal.
Para essa verificação é importante também observarmos que a quantidade de elementos da amostra fora do intervalo [-1,96;1,96] não deve ultrapassar 5%.
Desse modo, temos:
- 17 elementos então entre -1 e 1, ou seja 68%;
- 22 elementos então entre -1,64 e 1,64, ou seja 88%;
- 23 elementos então entre -1,96 e 1,96, ou seja 92%;
- 2 elementos fora do intervalo -1,96 e 1,96, ou seja 08%.
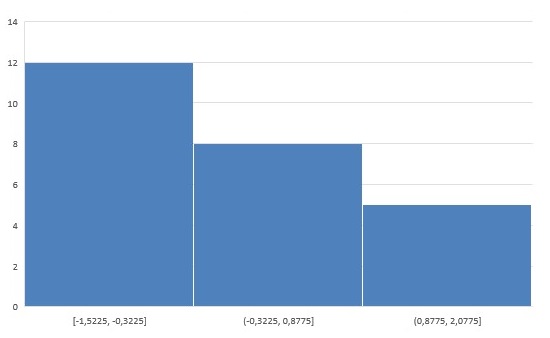
Com esse resultado podemos inferir a o modelo não está obedecendo a distribuição normal e, portanto, devemos eliminar o dado mais afastado da média, que pode ser tanto o dado 1 como o dado 9.
Passo 05: Otimização da amostra
Para esse exemplo, eliminaremos o dado 9 e repetiremos o processo até que a quantidade de elementos fora do intervalo [-1,96;1,96] fique menor ou igual a 5%, sempre verificando a cada retirada se os erros do modelo e das variáveis estão dentro dos valores aceitáveis (5% e 30%, respectivamente).
Vale lembrar que tarefa de avaliar imóveis por meio da inferência estatística não é algo muito simples e, por isso, recomendamos o uso de softwares específicos para lhe ajudar nisso.
Resumidamente, o processo deverá ser repetido 7 vezes, eliminando os dados 1, 2, 9, 13, 14, 19 e 20, restando 18 elementos na amostra.
Passo 05: Verificações da amostra otimizada
- Correlação entre as variáveis independentes
Tabela 2 – Matriz de correlação
| Frente terreno | Fundos (lateral) | Dist. ao centro (m) | Preço unitário (R$/m²) | |
| Frente (m) | 1 | |||
| Profundidade (m) | -0,0983 | 1 | ||
| Dist. ao centro (m) | -0,0318 | 0,3456 | 1 | |
| Preço unitário (R$/m²) | -0,2297 | 0,0367 | -0,8649 | 1 |
Ao analisar a matriz de correlação acima, podemos inferir que a correlação entre as variáveis independentes é baixa e menor que 0,80, o que significa que podem ser utilizadas juntas no modelo.
- Erros das variáveis independentes
\mathrm{(valor-P)_{frente}=0,03}% < 30% ⇒ OK!
\mathrm{(valor-P)_{profundidade}=0,77}% < 30% ⇒ OK!
\mathrm{(valor-P)_{profundidade}=0,04}% < 30% ⇒ OK!
- Erro do modelo
\mathrm{F\:de\: significação=0,00}% ≤ 5% ⇒ OK!
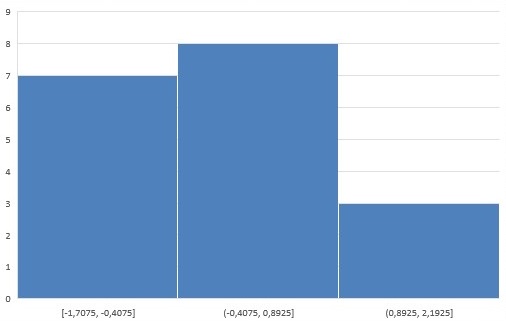
- Normalidade da amostra
- 12 elementos então entre -1 e 1, ou seja 66,67%;
- 16 elementos então entre -1,64 e 1,64, ou seja 88,89%;
- 18 elementos então entre -1,96 e 1,96, ou seja 100%;
- Nenhum outlier.
Passo 06: Equação de regressão
Satisfeitos todos os testes, iremos agora determinar a equação de regressão por meio dos coeficientes fornecidos pela tabela ANOVA de regressão.
Dessa forma, temos:
PREÇO UNITÁRIO (R$/m²) = 108,2699 – 1,8621 * FRENTE TERRENO (m) + 1,7848 * PROFUNDIDADE TERRENO (m) – 0,3233 * DIST. AO CENTRO (m)
Passo 07: Elaboração da PVG
Agora que já temos conhecimento da equação de regressão, estamos aptos a finalmente elaborar a Planta de Genérica de Valores do setor avaliando.
Para isso, devemos lembrar que:
- A Quadra 01 é composta por dois tipos de lotes: 20 m x 32 m e 20 m x 30 m;
- A Quadra 02 é composta por dois tipos de lotes: 15 m x 40 m e 17 m x 40 m;
- A Quadra 03 é composta por dois tipos de lotes: 20 m x 30 m e 15 m x 45 m.
Desse modo, temos:
Tabela 3 – Preço unitário resultante
| Quadra | Terreno | Variáveis independentes (m) | Valor Unitário (R$/m²) | |
| Distância ao centro | 100 | |||
| 01 | 20 m x 32 m | Frente | 20 | 95,81 |
| Profundidade | 32 | |||
| 20 m x 30 m | Frente | 20 | 92,24 | |
| Profundidade | 30 | |||
| Distância ao centro | 200 | |||
| 02 | 15 m x 40 m | Frente | 15 | 87,06 |
| Profundidade | 40 | |||
| 17 m x 40 m | Frente | 17 | 83,34 | |
| Profundidade | 40 | |||
| Distância ao centro | 300 | |||
| 03 | 20 m x 30 m | Frente | 20 | 27,57 |
| Profundidade | 30 | |||
| 15 m x 45 m | Frente | 15 | 63,65 | |
| Profundidade | 45 | |||
Tabela 4 – Resultado da avaliação em massa
| Quadra | Área do terreno (m²) | Valor Unitário (R$/m²) | Valor Venal (R$) |
| 1 | 640 | 95,81 | R$ 61.316,92 |
| 600 | 92,24 | R$ 55.342,83 | |
| 2 | 600 | 87,06 | R$ 52.237,72 |
| 680 | 83,34 | R$ 56.670,26 | |
| 3 | 600 | 27,57 | R$ 16.542,04 |
| 675 | 63,65 | R$ 42.965,75 |
Desse modo, a Planta de Valores resultante da nossa avaliação em massa é a seguinte:
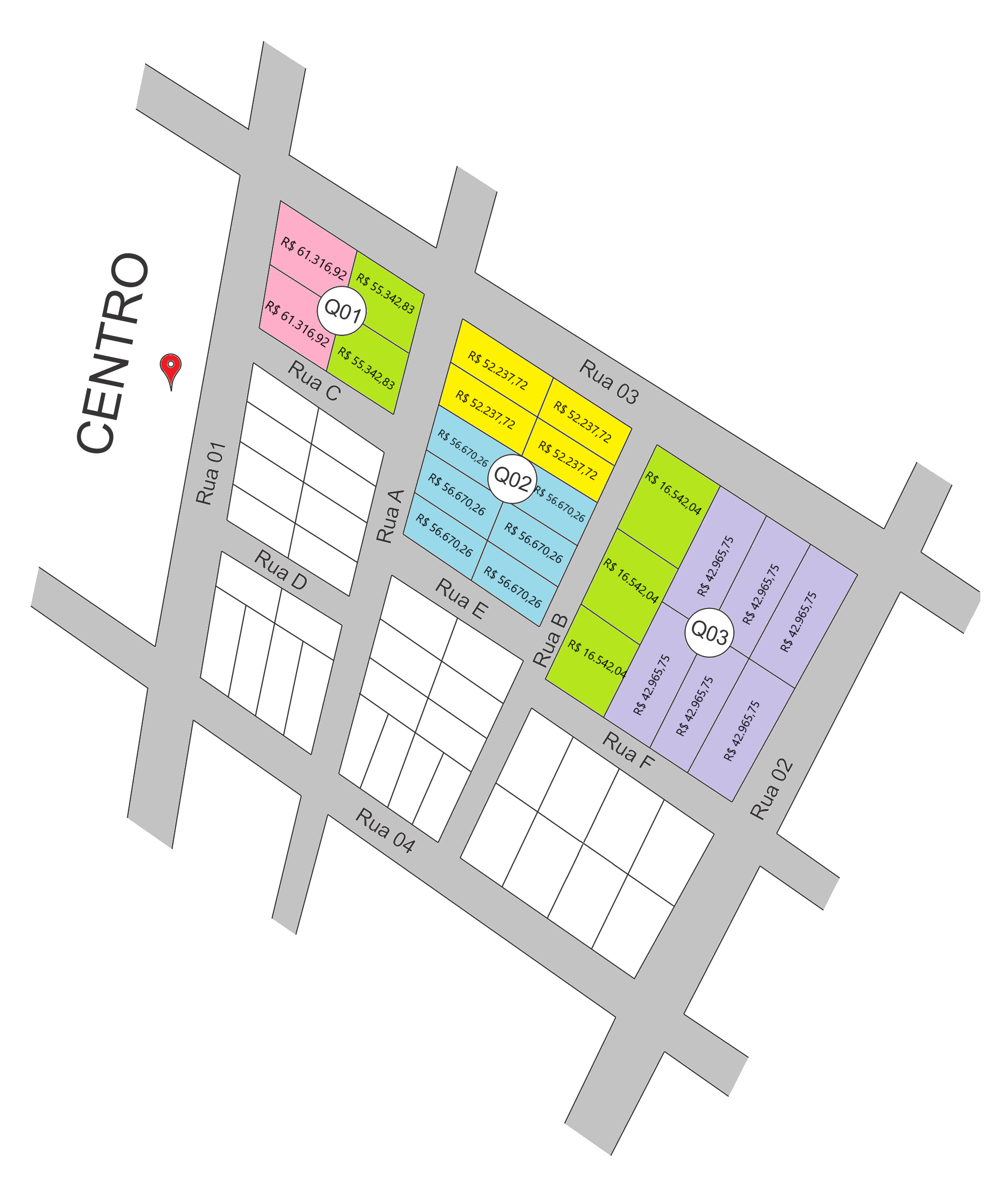
.
.
Pois bem, avaliadores, esse foi um breve exemplo hipotético de como dever ser feita uma avaliação em massa de imóveis urbanos, na prática, por meio da Inferência Estatística. E para te ajudar ainda mais, preparamos um e-Book gratuito sobre Avaliação Individual de Imóveis Urbanos.
[ebook-avaliacao-imoveis]É claro, no entanto, que esse universo é muito mais amplo do que conseguimos abordar em um e-Book.
Então, se você quiser se aprofundar mais nessa área, sugiro que conheça o curso online Formação de Peritos Judiciais em Avaliação de Imóveis de um dos nosso parceiros, o professor Fernando Sarian, que tem mais de 17 anos de experiência na área.
Nesse curso, você irá conhecer as norma vigentes, aprenderá sobre o Avaliação Imobiliária e, o melhor de tudo, aprenderá a elaborar seu próprio laudo técnico de avaliação. Tudo isso dando um enfoque especial na área pericial e nas legislações de interesse.
Ficou curioso? É só clicar aqui.
Dito isso, ficamos por aqui e se gostou você gostou, não deixa de seguir a gente no Instagram e também no Youtube para receber todas as novidades.
E se ainda ficou com alguma dúvida, deixe aqui nos comentários. Até o próximo post!
Fonte:
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-2: Avaliação de bens – Parte 2: Imóveis urbanos. Rio de Janeiro, 2011. 62 p.
BRASIL. Ministério das Cidades. Avaliação em massa para fins fiscais: Discussão, análise e identificação de soluções para problemas e casos práticos. Brasília. Ministério da Cidades, 2012.
RAGONE, Adriana. Planta genérica de valores: Elaboração. Teresina: IPOG, 2019.
.

Engenheira Civil pela Universidade Federal do Piauí, engenheira de obra, perita judicial e pós-graduanda em Avaliação, Auditoria e Perícias de Engenharia.