Ações e combinações em estruturas de madeira

A madeira é, provavelmente, o material de construção mais antigo dada a sua disponibilidade na natureza e sua facilidade de manuseio. Além disso, tem excelente relação resistência/peso e é também um ótimo isolante térmico.

Dessa forma, mesmo com os diversos materiais disponíveis no mercado, a madeira ainda é largamente utilizada nas edificações, principalmente na construção de telhados e na confecção de formas para concreto.

Sendo assim, é imprescindível a um bom construtor um conhecimento acerca das estruturas de madeira e é o que você encontrará aqui, no Guia.

Nesse post, você aprenderá como calcular as ações em uma estrutura de madeira, tanto no estado limite último como no estado limite de serviço, bem como calcular a resistência de projeto necessária, segundo a ABNT NBR 7190/97.

Para aprender a dimensionar uma estrutura de madeira, clique aqui.

Boa leitura!

Estado limite último

É o estado da estrutura que determinam a paralisação do seu uso, no todo ou em parte.

Se quiser saber mais sobre Estados Limites em estruturas, clique aqui.

Agora, iremos apresentar as expressões para o cálculo das solicitações no estado limite ultimo para três situações diferentes:

Combinações normais

\mathrm{F_d=∑ γ_{gi}F_{gi,k}+γ_{q}(F_{q1,k}+∑ψ_{0j}F_{qj,k})}

Onde:

• F_d: é a ação resultante, calculada no ELU;
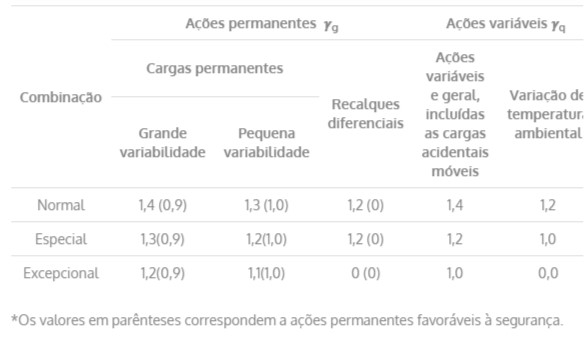
• 𝛾_gi: é o coeficiente de majoração das ações permanentes (tabela 1);
• 𝛾_q: é o coeficiente de majoração das ações vaiáveis (tabela 1);
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal;
• ψ_0j.F_qj,k: representa os valores reduzidos de combinação das demais ações variáveis.

Combinações especiais

\mathrm{F_d=∑ γ_{gi}F_{gi,k}+γ_{q}(F_{q1,k}+∑ψ_{0j,ef}F_{qj,k})}

Onde:

• F_d: é a ação resultante, calculada no ELU;
• 𝛾_gi: é o coeficiente de majoração das ações permanentes, tabela 1;
• 𝛾_q: é o coeficiente de majoração das ações vaiáveis, tabela 1;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal para a situação transitória;
• F_qj,k: representa os valores das demais ações variáveis;
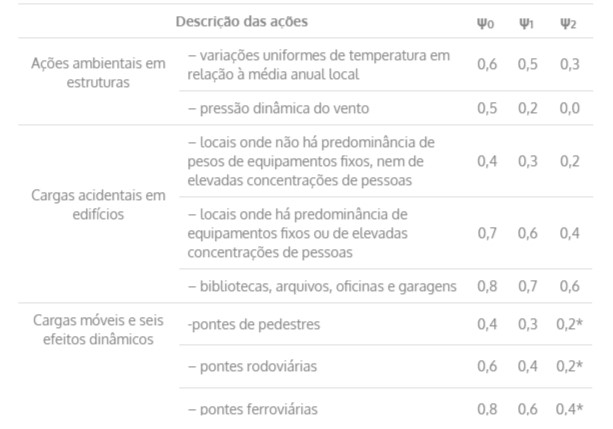
• ψ_0j,ef: é o fator de combinação (ψ_0j,ef =ψ_0j nas combinações normais ou ψ_0j,ef = ψ_2j quando a ação principal F_q1 tiver um tempo de atuação muito pequeno), tabela 2.

Combinações excepcionais

\mathrm{F_d=∑γ_{gi}F_{qi,k}+F_{q,exc}+γ_{q}∑ψ_{0j,ef}F_{qj,k}}

Onde:

• F_d: é a ação resultante, calculada no ELU;
• 𝛾_gi: é o coeficiente de majoração das ações permanentes, tabela 1;
• 𝛾_q: é o coeficiente de majoração das ações vaiáveis, tabela 1;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal para a situação transitória;
• F_qj,k: representa os valores das demais ações variáveis;
• F_q,exc: representa o valor da ações transitória excepcional;
• ψ_0j,ef: é o fator de combinação (ψ_0j,ef =ψ_0j nas combinações normais ou ψ_0j,ef = ψ_2j quando a ação principal F_q1 tiver um tempo de atuação muito pequeno), tabela 2.

Tabela 1 – Coeficientes de majoração 𝛾

 

Tabela 2 – Fatores de combinação ψ₀ e de utilização ψ₁ (frequente) e ψ₂ (quase-permanente)

Estado limite de serviço

Estado limite de serviço é o estado que causa efeitos estruturais que não respeitam as condições especificadas para o uso normal da construção ou que dá indícios de comprometimento da sua durabilidade.

No projeto, usualmente devem ser considerados os estados limites de utilização caracterizados por deformações excessivas e vibrações de grande amplitude.

Nesse estado limite, as ações são combinadas sem majoração e os valores característicos das ações variáveis são multiplicados pelos fatores ψ para se obter valores frequentes ou quase-permanentes. Essas combinações são representadas abaixo.

Combinação de longa duração

\mathrm{F_{d,uti}=∑F_{gi,k}+∑ψ_{2j}F_{qj,k}}

Onde:

• F_d,uti: é a ação resultante, calculada no ELS;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal para a situação transitória;
• F_qj,k: representa os valores das demais ações variáveis;
• ψ_2j: é o fator de utilização, tabela 2.

Combinação de média duração

\mathrm{F_{d,uti}=∑F_{gi,k}+ψ_{1}F_{q1,k}+∑ψ_{2j}F_{qj,k}}

Onde:

• F_d,uti: é a ação resultante, calculada no ELS;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal para a situação transitória;
• F_qj,k: representa os valores das demais ações variáveis;
• ψ₁: é o fator de utilização frequente, tabela 2;
• ψ_2j: é o fator de utilização quase-permanente, tabela 2;

Combinação de curta duração

\mathrm{F_{d,uti}=∑F_{gi,k}+F_{q1,k}∑ψ_{1j}F_{qj,k}}

Onde:

• F_d,uti: é a ação resultante, calculada no ELS;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q1,k: representa o valor característico da ações variável considerada como principal para a situação transitória;
• ψ₁: é o fator de utilização frequente, tabela 2.

Combinação de duração instantânea

      \mathrm{F_{d,uti}=∑F_{gi,k}+F_{q,especial}+∑ψ_{2j}F_{qj,k}}

Onde:

• F_d: é a ação resultante, calculada no ELS;
• F_gi,k: representa o valor característico das ações permanentes;
• F_q,especial: representa o valor característico da ações variável considerada como principal para a situação transitória;
• F_qj,k: representa os valores das demais ações variáveis;
• ψ_2j: é o fator de utilização, tabela 2.

Resistência

Agora, iremos descobrir como calcular a resistência de projeto da madeira, no estado limite último.

Primeiramente, para se determinar a resistência de cálculo é necessário calcular antes a resistência característica da madeira, que é o resultado do ensaio de resistência na direção paralela às fibras e é feito com corpos de prova isentos de defeitos.

Como esses resultados seguem uma distribuição aproximadamente gaussiana, usa-se a resistência característica fk, como sendo o valor abaixo do qual se encontram apenas 5% dos resultados.

Os resultados dos ensaios, no entanto, não representam as propriedades mecânicas da madeira serrada utilizadas em estruturas, pois estas variam com o teor de umidade, tempo de duração da carga e com a ocorrência de defeitos.

A resistência característica da madeira é, então, calculada conforme abaixo.

Resistência característica

 \mathrm{\dfrac{fk}{fm} = 0,70}

Onde:

• fk é a resistência característica (kN/m²);
• fm é o valor médio de resistência da madeira (kN/m²).

Resistência de cálculo

\mathrm{fd=Kmod\dfrac{fk}{γ_w}}

Onde:

• f_d: é a resistência de cálculo (kN/m²);
• fk é a resistência característica (kN/m²);
• 𝛾_𝑊: é o coeficiente de majoração, tabela 1;
• Kmod: é um coeficiente que ajusta os valores da resistência em função da influência de diversos fatores e é dado por: Komod = Kmod1 . Kmod2 . Kmod3;
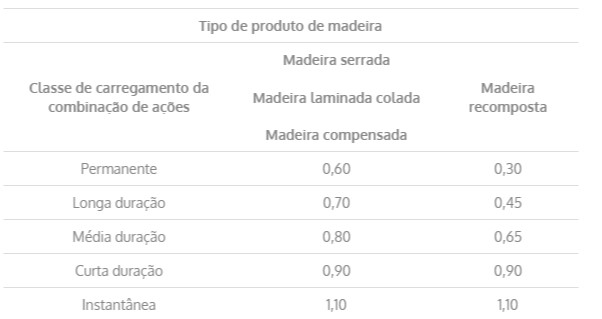
• Kmod1: leva em conta o tipo de produto de madeira e o tempo de duração da carga, tabela 3;
• Kmod2: considera o efeito da umidade, tabela 5;
• Kmod3: leva em conta a classificação estrutural da madeira, tabela 6.

Tabela 3 – Valores do Coeficiente Kmod1

 

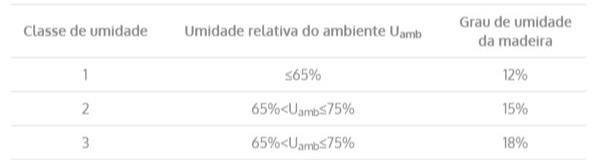
Tabela 4 – Classes de umidade

 

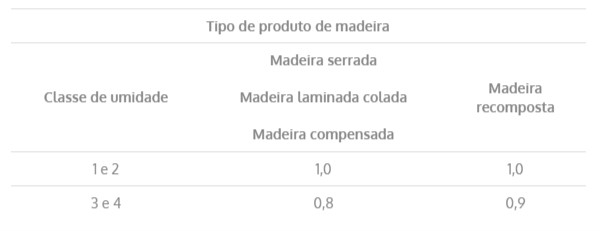
Tabela 5 – Valores do Coeficiente Kmod2

 

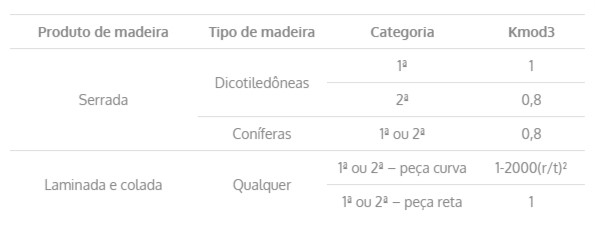
Tabela 6 – Valores do Coeficiente Kmod3

 

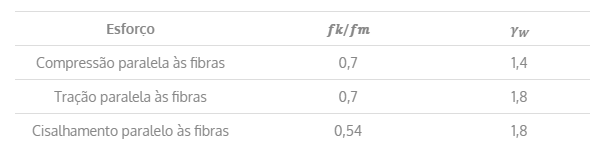
Tabela 7 – Valores do coeficiente 𝜸_𝑾

Módulo de elasticidade

O módulo de elasticidade é característico de cada material e é usado para medir as rigidezes. Ele varia com a composição química, microestrutura e defeitos existentes e pode ser obtido pela razão entre a tensão exercida e a deformação sofrida pelo material.

Para a madeira, o módulo de elasticidade efetivo é função do seu valor médio e é dado por:

\mathrm{\dfrac{E_{c,ef}}{E_c}=Kmod}

Onde:

• E_c,ef: é o valor real do módulo de elasticidade da madeira, que considera sua deformação lenta ao longo do tempo, também chamada de fluência (MPa);
• Kmod: é um coeficiente que ajusta os valores da resistência em função da influência de diversos fatores e é dado por: Komod = Kmod1 . Kmod2 . Kmod3;
• E_c: é o valor médio do módulo de elasticidade obtido de ensaios de compressão paralela às fibras que leva em conta apenas a deformação instantânea da madeira (MPa).

Exemplo prático

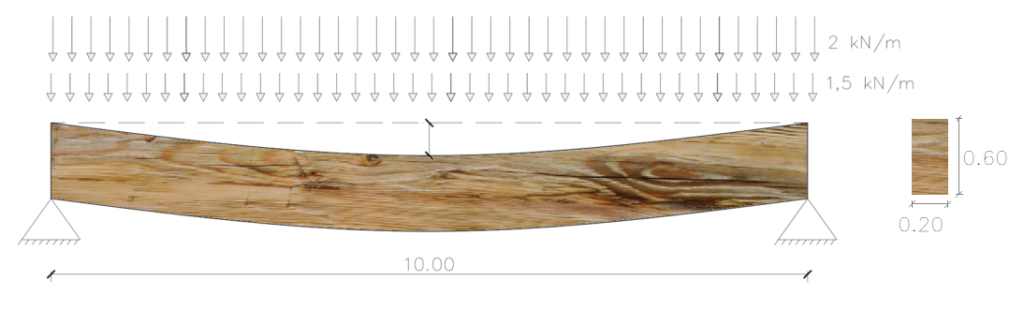
Uma viga biapoiada de madeira Jatobá (Ec=23607 MPa) laminada colada em ambiente de classe 3 de umidade está sujeita às seguintes cargas uniformemente distribuídas: Fg= 2kN/m e Fq=1,5kN/m.

Sendo o vão igual a 10m, verificar o estado limite de deformação excessiva.

RESOLUÇÃO:

Passo 01: Cálculo do Kmod

Madeira laminada colada e ação de longa duração: Kmod1=0,7 (tabela 3)

Madeira laminada colada classe 3 de umidade: Kmod2=0,8 (tabela 5)

Madeira laminada colada tipo qualquer, peça reta: Kmod3=1,0 (tabela 6)

\mathrm{Kmod=0,7.0,8.1,0=0,56}

Passo 02: Deslocamento máximo

De acordo com a tabela abaixo, baseada no item 9.2 da NBR 7190/97, temos:

Tabela 8 – Deslocamentos limites verticais

Como a viga é biapoiada de o vão é 10m e está sob efeito de ações permanentes e variáveis de longa duração, temos:

\mathrm{δ_{lim}=l/200=10/200=0,05m=50mm}

Passo 03: Combinação das ações

Como deseja-se verificar a deformação excessiva, a combinação das ações deverá ser feira no estado limite de utilização para combinações de longa geração:

\mathrm{F_{d,uti}=∑F_{gi,k}+∑ψ_{2j}F_{qj,k}}

Para determinar o valor de ψ_2j, usaremos a tabela 2. A ação é acidental e consideraremos que o local não há predominância de pesos, dessa forma:

ψ_2j=0,2

\mathrm{F_{d,uti}=2+0,2.1,5=2,30kN/m}

O valor da carga distribuída a se considerar para a fluência será de 2,3kN/m.

Passo 04: Deslocamento instantâneo

A fecha instantânea da viga será calculada por meio da equação da linha elástica para vigas biapoiadas.

\mathrm{δ_c=\dfrac{5.q.L^4}{384.E_c.I}}

\mathrm{δ_c=\dfrac{5.(2,3.{10}^3).{10}^4}{384.(20607.{10}^6).(3,6.{10}^{-3})}}

\mathrm{δ_c=3,5mm}

Passo 05: Deslocamento por fluência

O deslocamento real, calculado com Ec,ef, pode ser avaliado corrigindo-se o valor instantâneo de 3,5mm proveniente de uma carga uniforme, calculado com Ec acima, pela razão E_c/E_c,ef:

\mathrm{\dfrac{E_{c,ef}}{E_c}=Kmod}

Por regra de três, temos:

\mathrm{\dfrac{E_{c,ef}}{δ_{c,ef}}=\dfrac{E_{c}}{δ_{c}}}

\mathrm{δ_{c,ef}=\dfrac{E_{c,ef}.δ_{c}}{E_{c}}}

\mathrm{δ_{c,ef}=\dfrac{3,5}{0,56}}

\mathrm{δ_{c,ef}=6,25mm < 50mm}

Como δ < δ_lim, a viga atende com folga ao critério de verificação de deformação excessiva.

 

Esse post baseou-se, entre outras fontes, no livro Estruturas de Madeira de Pfeil e Pfeil, indicamos para você que tem interesse em se aprofundar mais no assunto. Ah, e caso queira exercitar o que aprendeu nesse post, clique aqui.

E se ainda ficou com alguma dúvida, deixe nos comentários.