Você já se deparou com a necessidade de dimensionar uma fundação? A principal dúvida é sempre se o solo local suporta a carga advinda da fundação.
Para tal dimensionamento, precisamos determinar as tensões atuantes e resistentes do solo. Já vimos como devemos calcular as tensões geostáticas nos solos.
Neste post iremos dar seguimento a esse estudo e abordar um pouco sobre as tensões induzidas nos solos, ensinando quais os principais tipos e os métodos de cálculo das mesmas.
Tensões Induzidas
Tensões induzidas são aquelas provenientes de carregamentos aplicados ao maciço de solo, podendo ser esses carregamentos referentes a fundações, sobrecarga de utilização, tráfego de veículos, etc.
Fazendo uso da Teoria da Elasticidade e considerando o solo como uma material homogêneo e elástico é possível determinar satisfatoriamente as variações nos estados de tensão do solo, embora os resultados obtidos para as deformações não sejam confiáveis para esse método.
A seguir, iremos apresentar algumas tipologias de carregamentos aplicados aos solos.
Para cada tipologia iremos apresentar a formulação para o cálculo da tensão e um exemplo para melhor entendimento e fixação.
Carga pontual sobre a superfície do maciço
Para o cálculo da tensões induzidas por esse tipo de carregamento, conforme ilustrado na figura abaixo, utiliza-se a equação de Boussinesq:
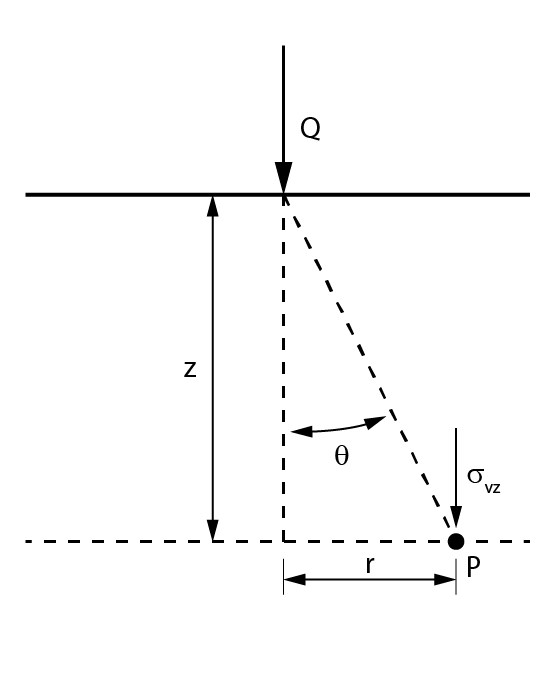
\mathrm{\sigma_{vz}=\dfrac{3\cdot Q\cdot z^3}{2\pi\cdot(r^2+z^2)^{5/2}}=\dfrac{3\cdot Q\cdot cos^3\theta}{2\pi \cdot z^2}}
Vale ressaltar que, como percebe-se pela formulação, a equação de Boussinesq independe do tipo de solo.
E você pode se perguntar: quando ocorrerá na prática uma carga pontual aplicada na superfície do solo?
É bastante usual, principalmente na fase de anteprojeto de fundações, é usual simplificar as cargas das fundações por cargas pontuais!
Exemplo
Qual o acréscimo de tensão nos pontos A e B ocasionado por uma carga pontual vertical de módulo 250 kN aplicada na superfície do solo?Sabe-se que os pontos estão há 2,0 m de profundidade.
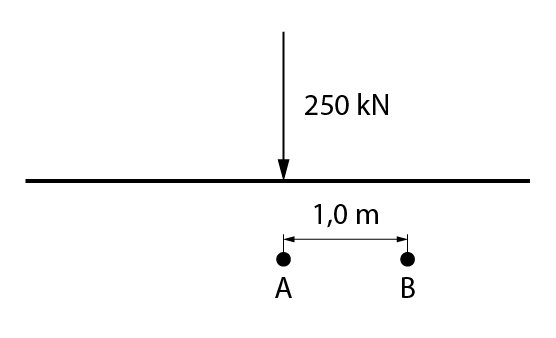
Para ambas as situações, basta aplicarmos a equação de Boussinesq.
Então, para o ponto A, temos:
\mathrm{\sigma_{vA}=\dfrac{3\cdot Q\cdot z^3}{2\pi\cdot(r^2+z^2)^{5/2}}}
\mathrm{\sigma_{vA}=\dfrac{3\cdot 250\cdot 2^3}{2\pi\cdot(0^2+2^2)^{5/2}}=29,86 kPa}
Para o ponto B, temos:
\mathrm{\sigma_{vB}=\dfrac{3\cdot Q\cdot z^3}{2\pi\cdot(r^2+z^2)^{5/2}}}
\mathrm{\sigma_{vB}=\dfrac{3\cdot 250\cdot 2^3}{2\pi\cdot(1^2+2^2)^{5/2}}=17,09 kPa}
Fundação circular, perfeitamente flexível
Para calcularmos as tensões induzidas por uma fundação circular, perfeitamente flexível e com carregamento uniformemente distribuído, em um ponto sob o centro da fundação devemos utilizar a Fórmula de Love:
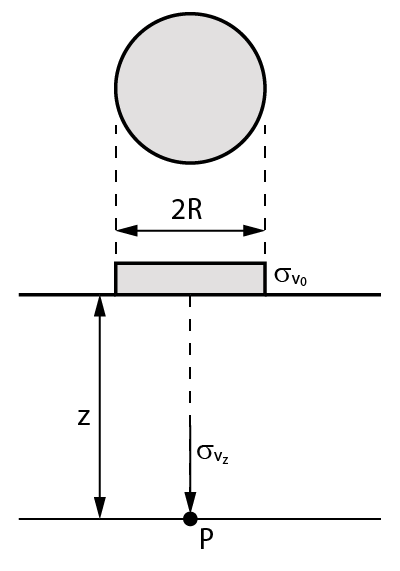
\mathrm{\sigma_{vz}=\sigma_{v_0} \cdot I}
Onde:
- \mathrm{\sigma_{vz}}: tensão vertical no ponto analisado;
- \mathrm{\sigma_{v_0}}: tensão uniformemente distribuída na fundação;
- I: fator de influência, que é calculado:
\mathrm{I=1-\left[\dfrac{1}{1+\left (\dfrac{R}{z}\right )^2}\right]^{3/2}}
Podemos perceber que o fator de influência, por depender unicamente dependente do raio da fundação e da profundidade do ponto analisado, pode ser facilmente tabelado.
Para um melhor entendimento, iremos resolver um exercício mais adiante utilizando tal formulação.
Fundação retangular, perfeitamente flexível e uniformemente carregada
Nesse caso, as principais soluções adotadas são a de Steinbrenner e de Newmark. Ambas são bem parecidas, dando o acréscimo de tensão em um ponto exatamente sob um dos vértices da fundação, a partir da formulação abaixo:
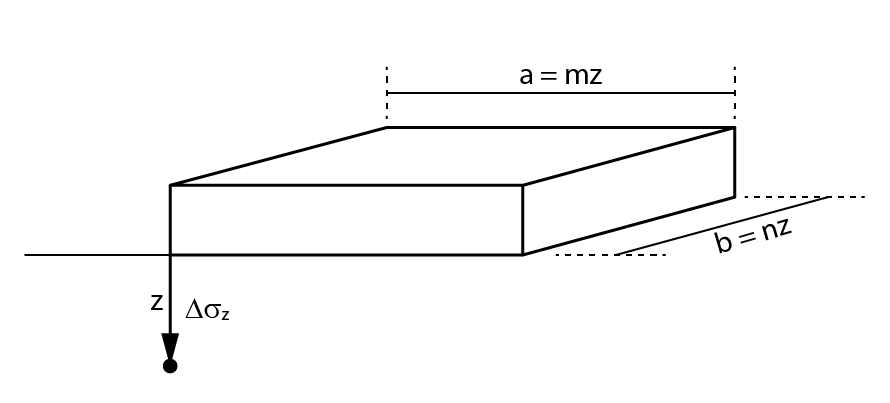
\mathrm{\Delta\sigma_{z}=\dfrac{\Delta q}{2\pi}\cdot P}
\mathrm{P=\left[arctg\dfrac{ab}{z\cdot R_3}+\dfrac{abz}{R_3}\cdot\left(\dfrac{1}{R_{1}^2}+\dfrac{1}{R_{2}^2}\right)\right]}
Onde:
- \mathrm{R_{1}=\left(m^2+z^2\right)^{1/2}}
- \mathrm{R_{2}=\left(n^2+z^2\right)^{1/2}}
- \mathrm{R_{3}=\left(m^2+n^2+z^2\right)^{1/2}}
Por simplificação, adota-se a resolução através do ábaco apresentado abaixo.
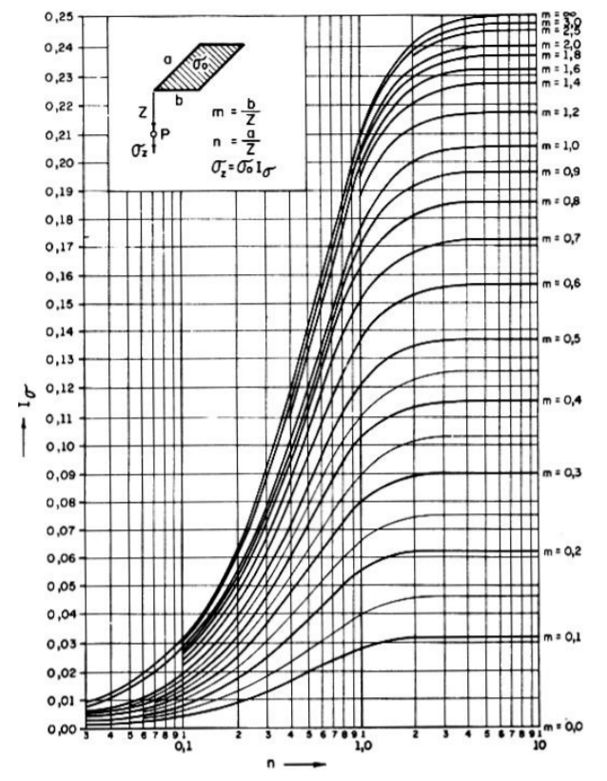
Os dados de entrada do ábaco são as relações entre a profundidade do ponto analisado e ambos lados da fundação, chamados de “m” e “n” que se encontram nas faces inferior e direita do ábaco.
O único dado de saída é o fator de influência “I”, de tal forma que:
\mathrm{\sigma_{z}=\sigma_{0} \cdot I}
Onde:
- \mathrm{\sigma_{z}}: tensão vertical no ponto analisado;
- \mathrm{\sigma_{0}}: tensão uniformemente distribuída na fundação;
- I: Fator de influência obtido pelo ábaco.
E aí, conseguiu entender tudo?
Para melhor fixação do conteúdo, apresentarei a seguir um exemplo resolvido do conteúdo apresentado nesse post.
Exemplo Proposto
Você pode acompanhar a resolução do exemplo proposto assistindo o vídeo abaixo ou simplesmente acompanhando a leitura do post!
Agora, vamos à questão:
Considere a vista em planta de duas fundações (uma circular e uma retangular) apresentada a seguir.
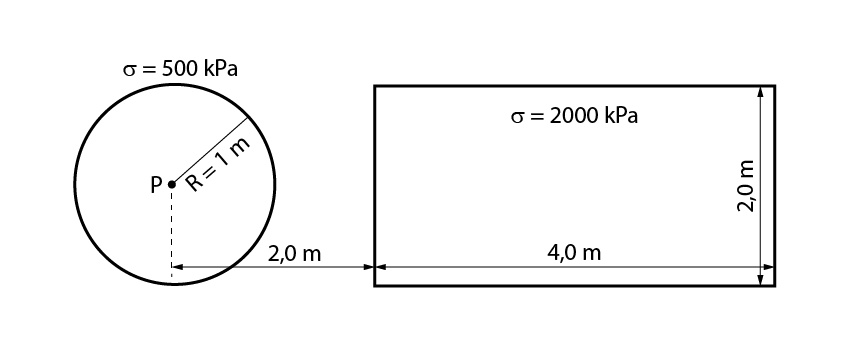
Calcule a tensão induzida por essas fundações em um ponto “P” localizado 2 m abaixo do centro da fundação circular.
Resolução
Passo 1
Então, inicialmente, vamos calcular a tensão induzida pela fundação circular, através da fórmula de Love:
\mathrm{\sigma_{z_{1}}=\sigma_{0} \cdot I}
\mathrm{I=1-\left[\dfrac{1}{1+\left (\dfrac{1}{2}\right )^2}\right]^{3/2}=0,284}
\mathrm{\sigma_{z_{1}}=500 \cdot 0,284}
\mathrm{\sigma_{z_{1}}=142 kPa}
Agora que já sabemos qual a tensão proveniente da fundação circular, iremos calcular a influência da fundação retangular.
Passo 2
Lembrando que através do ábaco de Newmark conseguimos determinar a tensão em um ponto sobre um dos vértices da fundação, precisamos encontrar alguma configuração em que o vértice da fundação circular seja o centro da fundação circular.
Para isso, faremos uso de fundações fictícias, da seguinte forma:
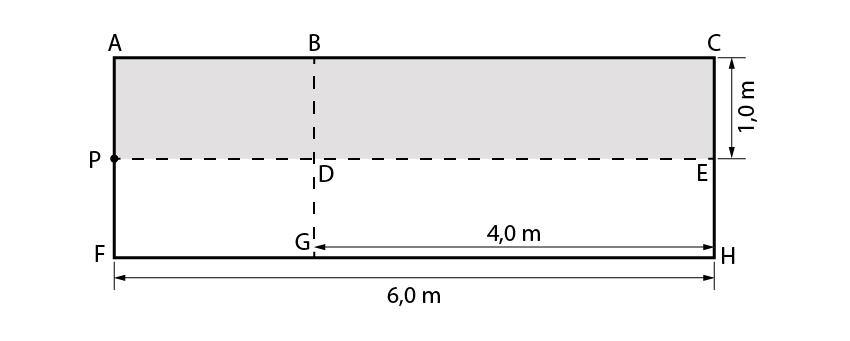
Nossa fundação analisada é a representada pelo retângulo BCHG. Que pode ser ainda entendida como 2 x BCED.
Como dito anteriormente, precisamos considerar fundações com algum vértice no ponto “P” analisado. Logo, podemos dizer que:
\mathrm{BCHG=2\cdot BCED}
\mathrm{2\cdot BCED=2 \cdot \left(ACEP - ABDP\right)}
Ou, em termos de fatores de influência, obtidos através do ábaco de Newmark:
\mathrm{I_{BCHG}=2\cdot I_{BCED}=2 \cdot \left(I_{ACEP} - I_{ABDP}\right)}
Passo 3
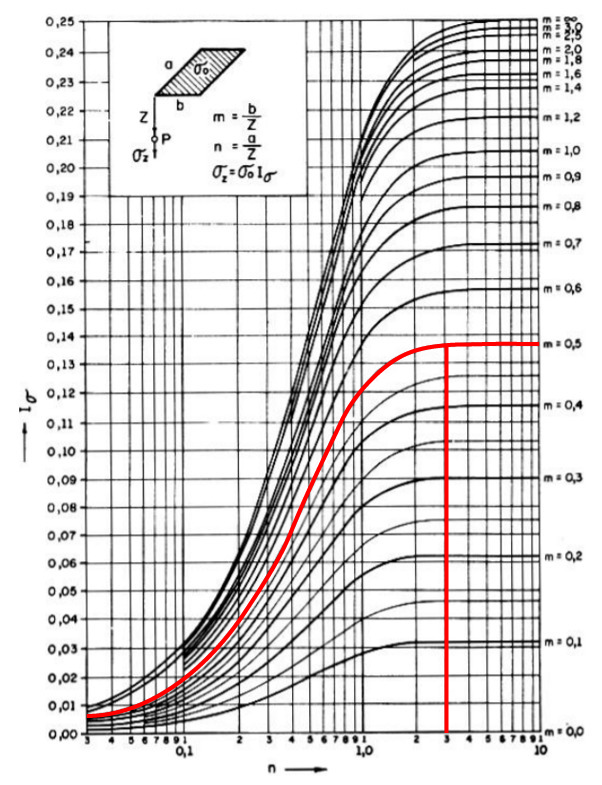
Vamos agora, então, determinar \mathrm{I_{ACEP}}, conforme figura acima e com o uso do ábaco de Newmark.
Calcularemos os dados de entrada no ábaco: m e n. Utilizando a=6,0m e b=1,0m, que são as dimensões da fundação representada por ACEP. Logo:
\mathrm{m=\dfrac{b}{z}=\dfrac{1}{2}=0,5}
\mathrm{n=\dfrac{a}{z}=\dfrac{6}{2}=3,0}
Fazendo a entrada de dados no ábaco, conforme ilustrado abaixo, encontramos o fator de influência I na face esquerda do ábaco:
\mathrm{I_{ACEP}=0,137}
Passo 4
Realizando o mesmo método, mas agora para analisar a fundação fictícia ABDP, temos:
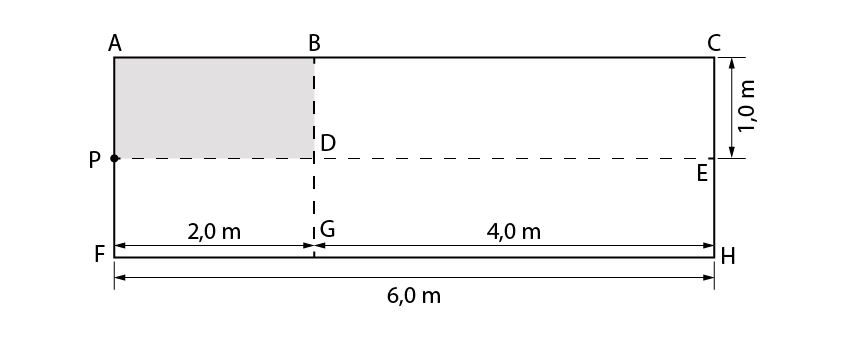
\mathrm{m=\dfrac{b}{z}=\dfrac{1}{2}=0,5}
\mathrm{n=\dfrac{a}{z}=\dfrac{2}{2}=1,0}
Fazendo a entrada de dados no ábaco encontramos o fator de influência I:
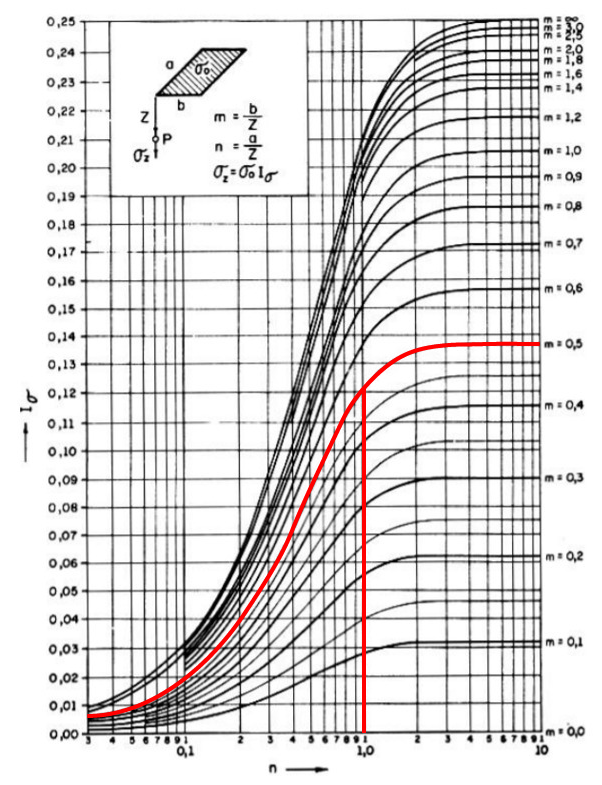
\mathrm{I_{ACEP}=0,121}
Agora já podemos determinar o fator de influência da nossa fundação analisada.
Como visto anteriormente:
\mathrm{I_{BCHG}=2\cdot I_{BCED}=2\cdot \left(I_{ACEP} - I_{ABDP}\right)}
\mathrm{I_{BCHG}=2\cdot \left(0,137 - 0,121\right)}
\mathrm{I_{BCHG}=0,032}
Logo, a tensão induzida pela fundação retangular é:
\mathrm{\sigma_{z_{2}}=\sigma_{0} \cdot I_{BCHG}}
\mathrm{\sigma_{z_{2}}=2.000\cdot 0,032}
\mathrm{\sigma_{z_{2}}=64 kPa}
Passo 5
Finalizando, a tensão induzida total no ponto P será a soma das tensões induzidas pela fundação circular e pela fundação retangular:
\mathrm{\sigma_{z}=142+64}
\mathrm{\sigma_{z}=206 kPa}
Esperamos que esse post tenha ajudado você a sanar todas suas dúvidas sobre tensões induzidas nos solos.
Se você tem interesse pela área de engenharia geotécnica e quer aprender ainda mais, indico o livro Mecânica dos Solos e suas Aplicações. O livro possui amplo conteúdo, leitura simples e que podem agregar bastante na sua formação.
Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
E não deixe de continuar seguindo nosso blog e de nos acompanhar também no YouTube.
Até a próxima, pessoal! =)
Fonte:
GERSCOVICH, D. M. S. Tensões em solos. Notas de aula. Rio de Janeiro, 2008.
CAPUTO, Homero Pinto. Mecânica dos solos e suas aplicações. Volume 1. 7ª edição. Rio de Janeiro, LTC, 2015.
DAS, Braja M. Fundamentos de engenharia geotécnica. São Paulo, Thomson Learning, 2007.
Engenheiro Civil, Especialista em Estruturas e Fundações. Ex-goleiro, Pseudosommelier de Cervejas e Poeta Freelancer Fajuto.

Amigo, parabéns pelo trabalho.
Abraços.
Eng. Ramon – Belo Horizonte
Opa, Ramon. Muito obrigado!
Abraço.
Felipe, é possível estimar através desse acréscimo de tensão o recalque em cada subcamada? Porque é possível ver uma “semelhança” na equação do método direto para estimativa de recalque inicial…
Bom dia, Guilherme. Tudo bem? O recalque de cada subcamada, de fato, é dependente da tensão nessa camada!
Para calcular o recalque em solos com várias camadas, recomendo que você utilize o método de Schmertmann.
Temos inclusive um post com uma questão resolvida. Dá uma conferida: https://www.guiadaengenharia.com/metodo-schmertmann-exercicio-resolvido/
Espero que tenha te ajudado!
Abraço.
Eu já tinha visto essa pagina, acho o site muito legal. Quanto a calcular o recalque utilizando os acréscimos de tensão, é porque queria levar em consideração as pressões de outras fundações próximas sobre a que estou calculando. E nas demais teoria não consegui nada parecido.
Entendi. No caso, seria interessante tentar analisar, por bulbo de tensões, a porcentagem de acréscimo de tensão das fundações vizinhas na camada analisada da fundação.
Acredito que seja a maneira mais simples de você fazer essa consideração.
Tenta aí, qualquer dúvida, pode me perguntar!
Abraço!
Parabéns, amigo! Muito bom sua síntese. Uma curiosidade: percebi que utilizou como fonte de consulta o material da Denise Gerscovich. Fui aluno dela, posso dizer que é uma excelente professora, porém suas turmas têm um alto índice de reprovação, extremamente difícil ser aprovado rs, um abraço