Se você já aprendeu a calcular a armação necessária de lajes nervuradas unidirecionais o próximo passo é verificar os estados limites de serviço (ELS). Nesse post verificaremos a deformação excessiva (ELS-DEF).
Limites e carregamentos de norma
A norma brasileira ABNT/NBR: 6118 (2014) informa, na Tabela 13.3, o deslocamento limite para aceitabilidade visual, que é 1 sobre 250 do vão. Sendo que, para esse limite, a norma indica que deve ser utilizado a combinação quase permanente:
\mathrm{F_D = F_G + \psi_2 \cdot F_Q}
Os valores de \mathrm{\psi_2} podem ser obtidos tanto na ABNT/NBR: 6118 (2014) quanto na ABNT/NBR: 8681 (2004) e para cargas acidentais valem:
| Situação | \mathrm{\psi_2} |
| Locais em que não há predominância de pesos e de equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas | 0,3 |
| Locais em que há predominância de pesos de equipamentos que permanecem fixos por longos períodos de tempo, ou de elevadas concentrações de pessoas | 0,4 |
| Bibliotecas, arquivos, depósitos, oficinas e garagens | 0,6 |
Ou seja, para obras residenciais, o carregamento utilizado na verificação da deformação excessiva deve ser o valor característico das cargas permanentes somando com o valor característico das cargas acidentais minorados por 0,3. Logo, para verificar os estados limites acima apresentados é necessário apenas calcular a flecha da laje devido a esse carregamento. A flecha máxima pode ser calculada através da equação diferencial da linha elástica.
As lajes nervuradas, conforme comentado em posts anteriores, usualmente são consideradas como simplesmente apoiadas e submetidas a carregamentos distribuídos ao longo de todo o vão. Dessa forma é possível obter o máximo deslocamento apresentado na laje pela equação abaixo:
\mathrm{\delta = \dfrac{5 \cdot p \cdot L^4}{384 \cdot E \cdot I}}
Modelo de Branson
Conforme estudado nos estádios de deformação do concreto armado a inércia de uma seção submetida a flexão simples pode variar drasticamente devido ao efeito da fissuração.
Mesmo o momento máximo atuante superando o momento de fissuração, tal solicitação só estará aplicada em algumas seções do elemento. Logo, as seções ao longo de toda a peça estarão trabalhando entre os estádios I e II. A norma brasileira ABNT/NBR: 6118 (2014) sugere o modelo de Branson (1968) para obter uma inércia equivalente para todo elemento a fim de considerar o efeito de fissuração:
\mathrm{I_{eq} = \left(\dfrac{M_r}{M_a} \right)^3 \cdot I_I + \left[ 1 - \left(\dfrac{M_r}{M_a} \right)^3 \right]\cdot I_{II}}
Efeito da fluência
Além da flecha imediata é necessário considerar as flechas surgidas pelo efeito da fluência. Esse efeito é caracterizado pelas deformações apresentadas ao longo do tempo por um elemento solicitado por uma tensão constante.
A norma brasileira recomenda o cálculo da flecha diferida no tempo pela multiplicação da flecha imediata por um fator \mathrm{\alpha_f}:
\mathrm{\alpha_f = \dfrac{\Delta \xi}{1+ 50 \cdot \rho '}}
Onde:
\mathrm{\rho ' = \dfrac{As'}{b \cdot d}}
\mathrm{\Delta \xi = \xi \left( t \right) -\xi \left( t_0 \right)}
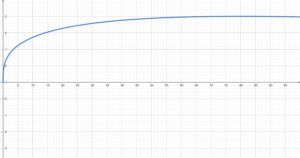
\mathrm { \xi (t) = \left\{ \begin{array}{ll} 0,68 \cdot 0,996^t \cdot t^{0,32}\; se\; t \leq 70 \\ 2\; se\; t\geq 70 \end{array} \right. }
Observe que para valores infinitos de tempo a norma limita o valor de \mathrm{\xi} em 2 devido a equação apresentada acima apresentar um ponto de máximo nesse valor, conforme pode ser observado na figura abaixo.
\mathrm{A_s} – área da armadura de compressão
\mathrm{t} – o tempo, em meses, quando se deseja o valor da flecha diferida
\mathrm{t_0} – a idade, em meses, relativa à data de aplicação da carga de longa duração
Por fim, a flecha diferida no tempo pode ser calculada com utilização da formulação abaixo:
\mathrm{\delta_{t,\infty} = \delta_{t,0} \cdot (1+\alpha_f )}
Obs1: A norma ainda permite compensar os deslocamentos com a aplicação de contraflechas. As mesmas devem ser limitadas a 1 sobre 350 do vão do elemento.
Obs2: É importante observar que a aplicação de Branson e as formulações de fluência não são válidas apenas para lajes nervuradas e podem ser utilizadas para outras seções submetidas a flexão simples.
Exemplo aplicado
Para o desenvolvimento desse exemplo, utilizaremos a mesma laje nervurada que já calculamos a armação utilizada. A mesma vence um vão de 3,0 m, possui enchimento cerâmico de 33 cm de largura por 8 cm de altura e possui 5 cm de capa. Os carregamentos já calculados na publicação anterior são:
Caso você prefira, é possível acompanhar essa resolução também por vídeo:
Carregamento e esforços solicitantes
\mathrm{g_{peso próprio}=0,3075 \; kN/m}
\mathrm{g_{revestimento}=0,45 \; kN/m}
\mathrm{g_{enchimento}=0,4752 \; kN/m}
\mathrm{q=0,675 \; kN/m}
Calculando inicialmente o carregamento quase permanente:
\mathrm{p = 0,3075+0,45+ \cdots}
\mathrm{+ 0,4752+0,3 \cdot 0,6750}
\mathrm{p=1,4352 \; kN/m}
Com esse carregamento temos que verificar o estádio em que a peça se encontra, uma vez que isso irá afetar a inércia da mesma e a flecha apresentada. Para isso, é necessário calcular a razão entre o momento de fissuração e o momento máximo atuante na laje.
\mathrm{M_a= \dfrac{1,4352 \cdot 3^2}{8}}
\mathrm{M_a = 1,6146 \; kN \cdot m = 161,46 \; kN \cdot cm}
Momento de fissuração
Para o cálculo das propriedades das lajes nervuradas pode-se levar em consideração as formulações apresentadas para seções no formato T.
\mathrm { f_{ct,m} = 0,3 \cdot {f_{ck}}^{\frac{2}{3}} = 0,3 \cdot 20^{\frac{2}{3}} }
\mathrm {f_{ct,m} = 2,21 \; MPa = 0,221 \; kN/cm^2}
\mathrm { M_r = \dfrac {\alpha \cdot f_{ct,m} \cdot I} {y_t} }
Área da seção homogeneizada:
\mathrm{A_g=(b_f-b_w) \cdot h_f + b_w \cdot h + \cdots}
\mathrm{+ A_s \cdot (\alpha - 1)}
\mathrm{A_g=(45-12) \cdot 5 + 12 \cdot 13 + \cdots}
\mathrm{+ 0,6 \cdot (9,865 - 1)}
\mathrm{A_g= 326,319 \; cm^2}
Centro de gravidade da seção homogeneizada:
\mathrm{y_{h}= \dfrac{(b_f-b_w) \cdot \dfrac{h_f^2}{2} + b_w \cdot \dfrac{h^2}{2}}{A_h} + \cdots}
\mathrm{+ \dfrac{A_s \cdot (\alpha - 1) \cdot d}{A_h}}
\mathrm{y_{h}= \dfrac{(45-12) \cdot \dfrac{5^2}{2} + 12 \cdot \dfrac{13^2}{2}}{326,319} + \cdots}
\mathrm{+ \dfrac{0,6 \cdot (9,865 - 1) \cdot 10,5}{326,319}}
\mathrm{y_{h}= 4,543 \; cm}
Momento de inércia à flexão da seção homogeneizada:
\mathrm{I_h = \dfrac{(b_f - b_w) \cdot h_f^3}{12} + \dfrac{b_w \cdot h^3}{12} + \cdots}
\mathrm{+ (b_f - b_w) \cdot h_f \cdot (y_h - \dfrac{h_f}{2})^2 + \cdots}
\mathrm{+ b_w \cdot h \cdot (y_h - \dfrac{h}{2})^2 + \cdots}
\mathrm{+ A_s \cdot (\alpha - 1) \cdot (y_h - d)^2}
\mathrm{I_h = \dfrac{(45 - 12) \cdot 5^3}{12} + \dfrac{12 \cdot 13^3}{12} + \cdots}
\mathrm{+ (45 - 12) \cdot 5 \cdot (4,543 - \dfrac{5}{2})^2 + \cdots}
\mathrm{+ 12 \cdot 13 \cdot (4,543 - \dfrac{13}{2})^2 + \cdots}
\mathrm{+ 0,6 \cdot (9,865 - 1) \cdot (4,543 - 10,5)^2}
\mathrm{I_h = 4015,641 \; cm^4}
Como a formulação de \mathrm{y_h} fornece a distância do centro de gravidade para o topo da seção e na equação do \mathrm{M_r} o \mathrm{y_t} significa a distância do centro de gravidade à fibra mais tracionada, devemos calcular o valor do mesmo (lembrando que a fibra mais tracionada encontra-se na face inferior, uma vez que a seção está solicitada a um momento fletor positivo):
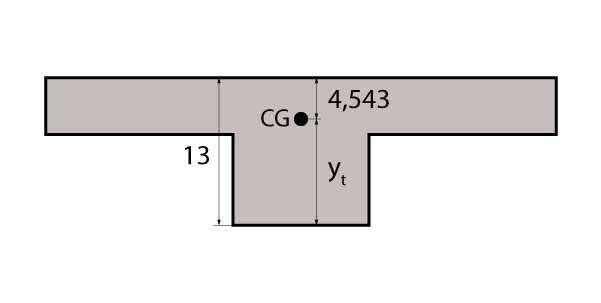
\mathrm{y_t = 13 - 4,543 = 8,457 \; cm}
\mathrm { M_r = \dfrac {\alpha \cdot f_{ct,m} \cdot I} {y_t} }
\mathrm { M_r = \dfrac {1,2 \cdot 0,221 \cdot 4015,641} {8,457}}
\mathrm { M_r = 125,925 \; kN \cdot cm}
Cálculo da inércia equivalente
Como o momento solicitante foi superior ao momento de fissuração, devemos corrigir a inércia da peça através da formulação de Branson:
\mathrm{I_{eq} = \left(\dfrac{M_r}{M_a} \right)^3 \cdot I_I + \left[ 1 - \left(\dfrac{M_r}{M_a} \right)^3 \right]\cdot I_{II}}
Para isso é necessário calcular antes a inércia no estádio II puro. Iniciando pela altura da linha neutra:
\mathrm{a= \dfrac{b_w}{2}}
\mathrm{a= \dfrac{12}{2} = 6}
\mathrm{b = h_f \cdot (b_f - b_w) + \cdots}
\mathrm{+ \alpha_e \cdot A_s}
\mathrm{b = 5 \cdot (45 - 12) + \cdots}
\mathrm{+ 9,865 \cdot 0,6}
\mathrm{b = 170,919}
\mathrm {c = - d \cdot \alpha_e \cdot A_s - \dfrac{h_f^2}{2} \cdot (b_f - b_w) }
\mathrm {c = - 10,5 \cdot 9,865 \cdot 0,6 - \dfrac{5^2}{2} \cdot (45 - 12) }
\mathrm {c = - 474,65 }
\mathrm{x_{II} = \dfrac{-b \pm \sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a}}
\mathrm{x_{II} = \dfrac{-170,919}{2 \cdot 6}} + \cdots
\mathrm{\pm \dfrac{ \sqrt{170,919^2 - 4 \cdot 6 \cdot (-474,65)}}{2 \cdot 6}}
\mathrm { x_{II} = \left\{ \begin{array}{ll} 2,549 \; cm \\ -31,035 \; cm \end{array} \right. }
Partindo agora para o cálculo do momento de inércia para o estádio II puro:
\mathrm{I_{II} = \dfrac{b_f \cdot x_{II}^3}{3} + \alpha_e \cdot A_s \cdot (x_{II}-d)^2}
\mathrm{I_{II} = \dfrac{45 \cdot 2,549^3}{3} + \cdots}
\mathrm{+ 9,865 \cdot 0,6 \cdot (2,549-10,5)^2}
\mathrm{I_{II} = 622,62 \; cm^4}
A partir dos momento atuante máximo, momento de fissuração, inércia no estádio I e inércia no estádio II puro, é possível calcular uma inércia equivalente para todo o elemento:
\mathrm{I_{eq} = \left(\dfrac{125,93}{161,46} \right)^3 \cdot 4015,64 + \cdots}
\mathrm{+ \left[ 1 - \left(\dfrac{125,93}{161,46} \right)^3 \right]\cdot 622,62}
\mathrm{I_{eq}= 2233,51 \; cm^4}
Cálculo da flecha imediata
\mathrm{\delta = \dfrac{5 \cdot p \cdot L^4}{384 \cdot E \cdot I_{eq}}}
\mathrm{ \delta = \dfrac{5 \cdot 0,014352 \cdot 300^4}{384 \cdot 2128,74 \cdot 2233,51}}
\mathrm{ \delta = 0,32 \; cm}
Cálculo da flecha diferida no tempo
Analisando agora o fenômeno da fluência. Para o mesmo não será considerada a armação comprimida, o tempo de aplicação das cargas igual a 7 dias e o tempo final igual no limite acima de 70 meses:
\mathrm{t_0 = \dfrac{7}{30} = 0,23 \; meses}
\mathrm{t_{\infty} = 70 \; meses}
\mathrm{\xi (t_0) = 0,68 \cdot 0,996^t \cdot t^{0,32}}
\mathrm{\xi (0,23) = 0,68 \cdot 0,996^{0,23} \cdot {0,23}^{0,32}}
\mathrm{\xi (0,23) = 0,42}
\mathrm{\Delta \xi = \xi (t_{\infty}) - \xi (0,23)}
\mathrm{\Delta \xi = 2 - 0,42 = 1,58}
\mathrm{\alpha_f = \dfrac{\Delta \xi}{1+ 50 \cdot \rho '}}
\mathrm{\alpha_f = \dfrac{1,58}{1+ 50 \cdot 0} = 1,58}
Com o valor de \mathrm{\alpha_f} calculado é possível calcular a flecha diferida no tempo a partir da flecha imediata:
\mathrm{\delta_{t,\infty} = \delta_{t,0} \cdot (1+\alpha_f )}
\mathrm{\delta_{t,\infty} = 0,32 \cdot (1+1,58 )=0,83 \; cm}
Comparação com os deslocamentos limites
O valor de 0,83 cm seria o valor do máximo deslocamento vertical apresentado pela laje já considerando os efeitos da fissuração e da fluência. Observe que esse valor deve ser comparado com o deslocamento limite:
\mathrm{\delta_{lim} = \dfrac{L}{250} = \dfrac{300}{250} = 1,2 \; cm}
Para esse problema a laje respeitou a condição de deformação excessiva. É importante lembrar que ainda teríamos o recurso de aplicar uma contraflecha limitada a 0,85 cm (300/350) caso a laje apresentasse uma flecha um pouco superior ao limite admissível.
Nesse post você aprendeu a calcular os deslocamentos apresentados por lajes nervuradas considerando os efeitos da fissuração e da fluência e compara-los com os limites admissíveis na norma brasileira.
Se você gostou desse texto ou se ainda possui alguma dúvida, deixe uma mensagem nos comentários abaixo!
Otimize seus cálculos de engenharia em minutos. Experimente o Calculadoras de Engenharia.
