Ação do Vento em Estruturas: Distribuição e Exercícios Práticos [Guia Completo]

Se você já nos acompanha deve ter percebi a importância que damos a resolução de exercícios para o aprendizado. Julgamos ser uma excelente forma de consolidar o conhecimento.

Nessa publicação vamos aproveitar o que estudamos sobre repartição da força de arrasto em estruturas de concreto armado para continuarmos um exercício já iniciado anteriormente. O objetivo do exercício é repartirmos a Força de Arrasto apenas para uma das direções, deixando a outra para você fazer sozinho como forma de estudo.

Apresentação do problema

Até então, nós calculamos a pressão dinâmica em cada pavimento de um edifício com as dimensões em planta 20 m x 30 m e 18 m de altura. Agora, além das dimensões de base, para distribuirmos a Força de Arrasto também precisaremos alocar e pré-dimensionar os pilares e vigas.

A figura abaixo apresenta um arranjo para o pré-dimensionamento dos pilares, em que foram consideradas as dimensões 20 cm x 80 cm para os pilares centrais, 20 cm x 50 cm para os pilares laterais e 20 cm x 40 cm para os pilares de canto. Todas as vigas foram consideradas com as dimensões de 20 cm x 50 cm.

Caso tenha interesse em estimar também os elementos de sua estrutura, recomendo que confira nossa conteúdo sobre pré-dimensionamento de vigas, pilares e lajes.

Tenho mais uma vantagem para você, caso prefira, ainda pode conferir a resolução pelo vídeo abaixo:

Força de Arrasto do Vento

Para calcular a força de arrasto na estrutura, temos que obter inicialmente o coeficiente de arrasto para as duas direções. Na nossa edificação vamos considerar que atua um vento de alta turbulência.

Coeficiente de Arrasto

Nessa resolução faremos apenas o vento incidindo na direção da maior fachada, ou seja, considerando \mathrm{l_1 = 30}.

\mathrm{\dfrac{l_1}{l_2} = \dfrac{30}{20} = 1,5}

\mathrm{\dfrac{h}{l_1} = \dfrac{18}{30} = 0,6}

Ao entrar no ábaco para alta turbulência, chegamos na seguinte situação:

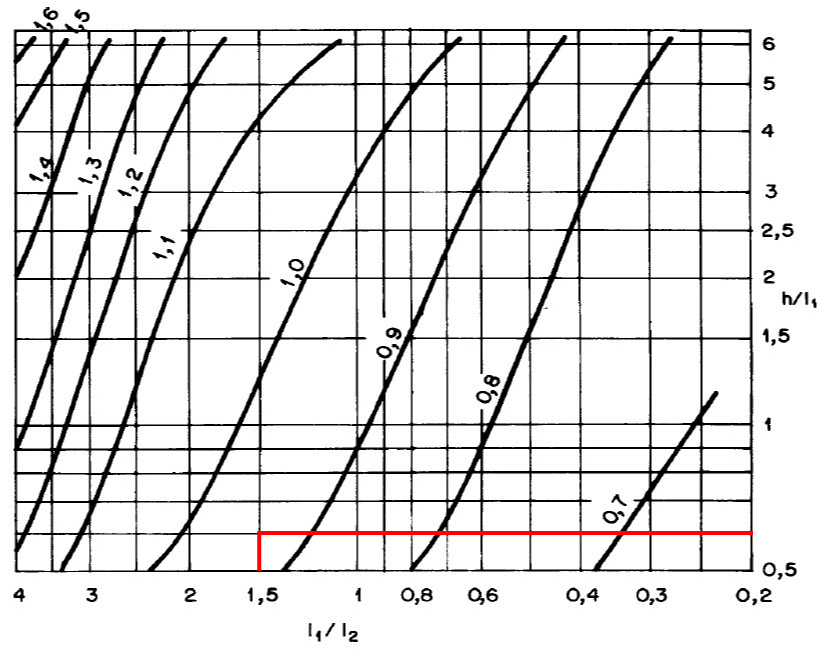
Assim sendo, como o ponto encontrado está entre as curvas 1,0 e 0,9, podemos ou utilizar o maior valor ou interpolar linearmente os valores. No nosso exemplo, utilizarei o valor de 0,95, que é uma interpolação aproximada.

Apenas para facilitar o acompanhamento dessa publicação, vou repetir as pressões dinâmicas em cada pavimento encontradas no exercício anterior:

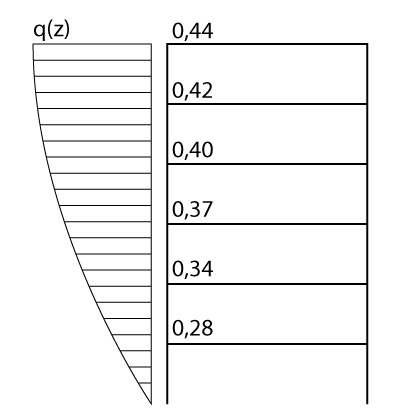
Agora utilizaremos a formulação abaixo para calcular a Força de Arrasto aplicada em cada pavimento.

\mathrm{F_a = C_a \cdot q \cdot A_e}

Área efetiva

O valor da área efetiva para o vento atuando na maior fachada vale o produto entre essa largura e o pé-direito do edifício. A figura abaixo destaca a área efetiva para o último pavimento e para o nível +9,0 m (que é similar aos demais).

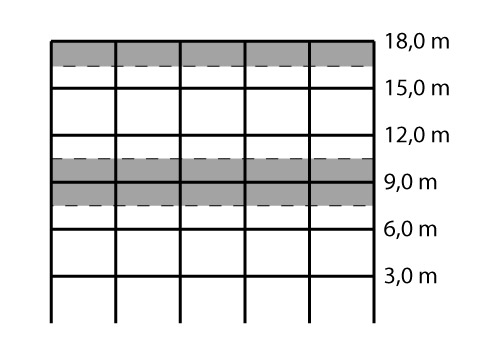
\mathrm{A_e = 30 \cdot 3 = 90 \; m^2}

Vale chamar atenção que o último pavimento possui uma área efetiva menor que os demais, devido a ter uma altura efetivo pela metade.

Agora devemos multiplicar cada um dos valores acima pelo coeficiente de arrasto e por sua área efetiva (esta só irá variar no último pavimento). A tabela abaixo apresenta a força horizontal do vento que atua em cada pavimento naquela direção.

z (m)	\mathrm{F_a \; (kN)}
		3,0	23,9
6,0	29,1
9,0	31,6
12,0	34,2
15,0	35,9
18,0	18,8

Apenas para melhorar o entendimento, vou repetir a mesma informação no formato de figura.

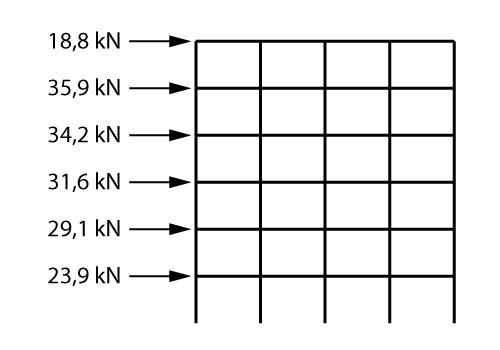
Apesar da figura acima apresentar um pórtico, o valor destacado atua em toda a estrutura naquele pavimento.

Repartição da ação do vento

Analisando a estrutura em questão percebemos que, na direção analisada, temos a presença de dois pórticos diferentes. O pórtico de extremidade se repete duas vezes e o pórtico central se repete quatro vezes, vide figura abaixo.

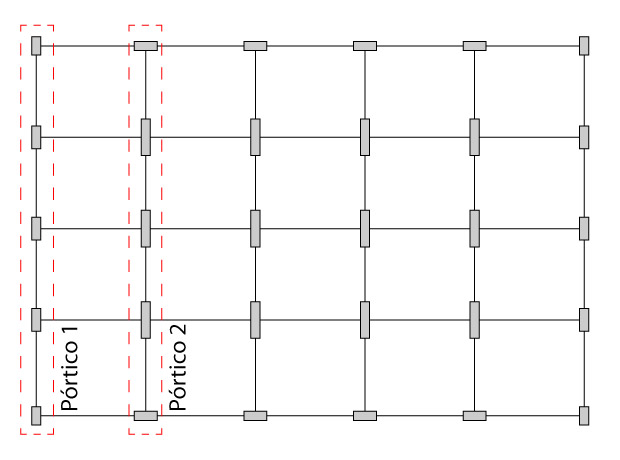
Análise dos Pórticos no Ftool

Os dois pórticos foram lançados no Ftool e submetidos a uma força horizontal de 100 kN no último pavimento (nó 31 da figura abaixo). Todas as barras dos dois pórticos foram lançadas com o mesmo módulo de elasticidade e as inércias correspondendo as dimensões reais do pilar.

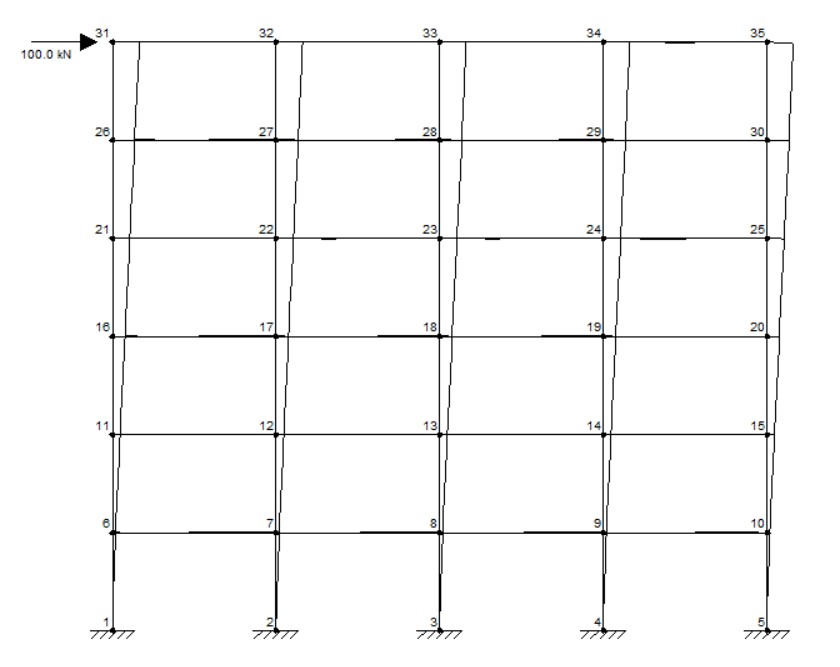
Para o pórtico de extremidade obtivemos um deslocamento no nó 35 de 15,95 mm e para o pórtico intermediário obtivemos um deslocamento, no mesmo nó, de 12,79 mm.

Aqui podemos partir para uma abordagem diferente da realizada com o processo de pilar equivalente. Como aplicamos a mesma força arbitrária e utilizamos o mesmo módulo de elasticidade, podemos calcular a proporção da força que vai para cada pórtico simplesmente pela proporção dos deslocamentos.

Repartição da Força de Arrasto

Vamos à prática calculando a relação entre os deslocamentos:

\mathrm{\dfrac{15,95}{12,79} = 1,247}

Se com o mesmo módulo de elasticidade e a mesma força horizontal arbitrária o pórtico de extremidade apresentou um deslocamento 24,7% superior ao pórtico central, este portanto, é 24,7% mais rígido do que o de extremidade.

Lembre-se que, essa força arbitrária que aplicamos e o deslocamento que obtivemos servem apenas para analisar a rigidez do pórtico como um todo. Na realidade, nem a força é de 100 kN condiz com a realidade nem os deslocamentos são diferentes entre os pórticos (devido ao efeito de diafragma rígido e a desconsideração da torção do edifício).

Dessa forma, vamos pensar o seguinte: se o pórtico central é 24,7% mais rígido que o pórtico de extremidade e assumndo que todos os pórticos no mesmo pavimento tem o mesmo deslocamento, o pórtico central tem que absorver 24,7% mais força que o pórtico de extremidade.

Logo, considerando a força que será aplicada apenas em um pórtico de extremidade como \mathrm{F^*}, a força a ser aplicada em um pórtico central será \mathrm{1,247 \cdot \; F^*}.

Assim sendo, a figura abaixo resume a proporção das forças absorvida entre os pórticos.

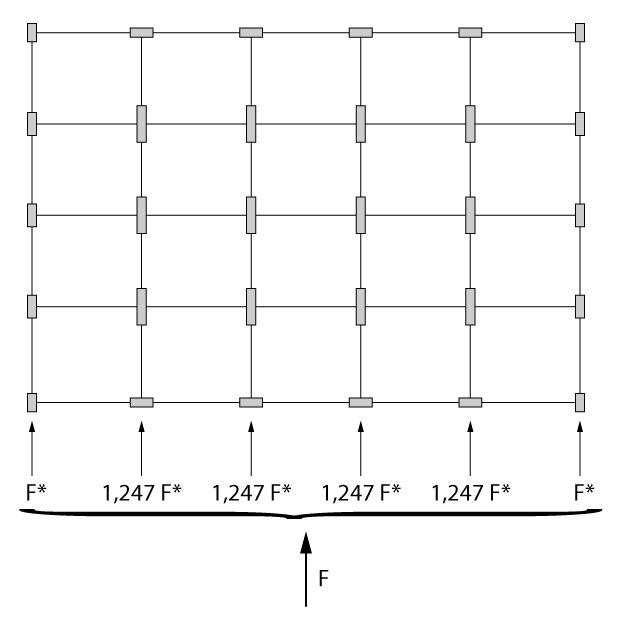
Consideramos aqui uma força qualquer \mathrm{F} como a força de arrasto de um pavimento, uma vez que temos várias forças de arrasto diferente (uma por pavimento), mas queremos apenas a distribuição entre os pórticos.

\mathrm{4 \cdot \left( 1,247 \cdot F^* \right) + 2 \cdot F^* = F}

\mathrm{F^* = 0,143 \cdot F}

Resultado da distribuição da ação do vento

Ou seja, após distribuir a Força de Arrasto, cada pórtico de extremidade recebe 14,3% do total e cada pórtico central recebe 17,85% da força de arrasto total.

Agora sim, podemos montar uma tabela com as forças a serem aplicada em cada pórtico e cada pavimento:

z (m)	\mathrm{F_a \; (kN)}	Força no pórtico de extremidade (kN)	Força no pórtico central (kN)
				3,0	23,9	3,42	4,27
6,0	29,1	4,16	5,19
9,0	31,6	4,52	5,64
12,0	34,2	4,89	6,10
15,0	35,9	5,13	6,41
18,0	18,8	2,69	3,36

Recado final

Parabéns por ter chegado até essa quarta publicação sobre ação do vento em estruturas. Com certeza agora você está mais um passo a frente no seu nível de conhecimentos sobre dimensionamentos de estruturas.

O próximo passo para esse assunto é estudar maneiras mais diretas para repartição das cargas de vento e também análises mais realistas, considerando a torção do edifício.