Dimensionamento de muro de gravidade: exemplo prático

Se você já leu nossos posts anteriores sobre muros de arrimo, determinação de empuxos do solo e etapas para o dimensionamento de um muro de gravidade, tenho certeza que você está preparado para esse post!

Agora nós iremos dimensionar um muro de arrimo de gravidade.

Vamos lá?

Apresentação do problema

Dimensionar um muro de gravidade em concreto ciclópico (\mathrm{\gamma_{conc} = 25kN/m^3}) para um desnível de 3,0 m, utilizando como solução um muro de seção escalonada. Dados do solo local:

• \mathrm{{\gamma _{solo}} = 19kN/m};
• Ângulo de atrito interno \mathrm{\varphi = 35};
• Coeficiente de atrito entre base do muro e solo \mathrm{\mu = 0,4};
• c=0 (areia pura);
• Tensão admissível de compressão do solo \mathrm{{\sigma _{adm}} = 150kN/m^2}.

Pré-dimensionamento do muro

Para o pré-dimensionamento do muro de gravidade escalonado, vamos utilizar os valores indicados no post sobre etapas de dimensionamento de um muro de gravidade.

Realizando o pré-dimensionamento como indicado no post anterior, teremos a seguinte configuração para o mesmo:

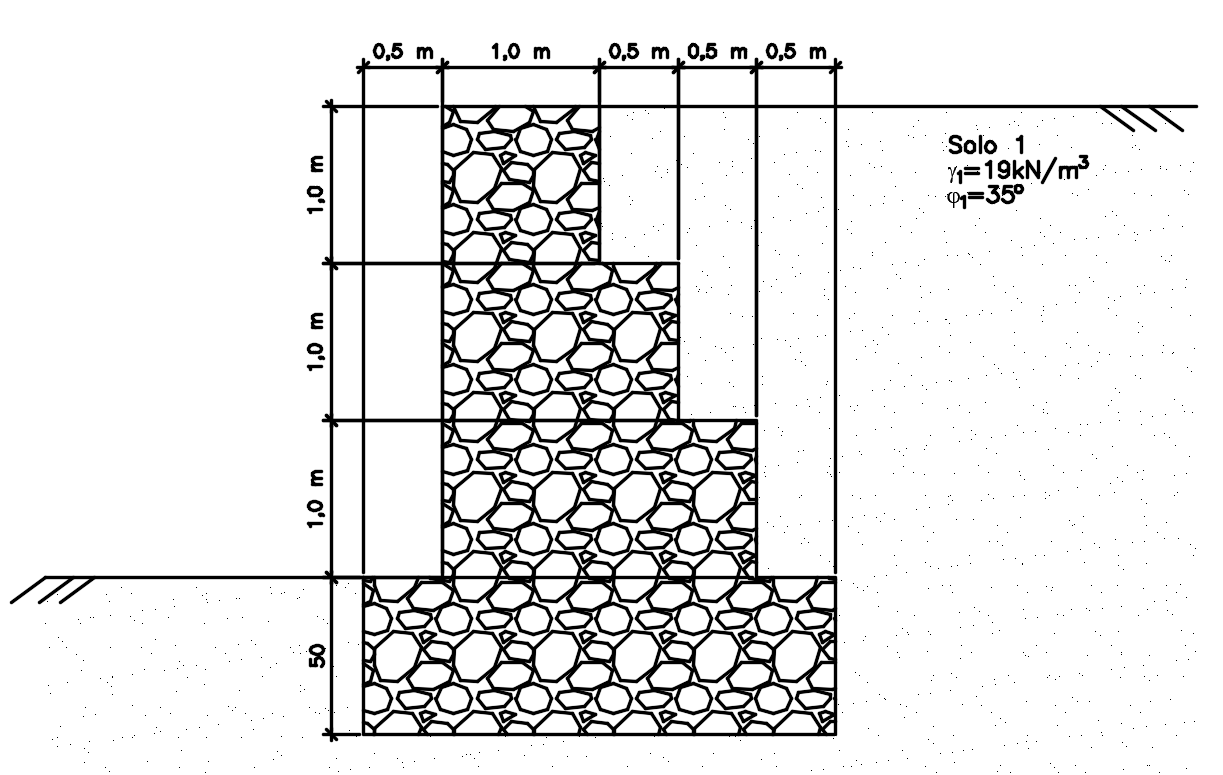
Agora que já fizemos o pré-dimensionamento, vamos para etapa de determinar as forças que estão atuando sobre o muro.

Determinação das forças atuantes

Para o muro de gravidade em questão, podemos dizer que as forças atuantes sobre o mesmo são:

• Empuxos do solo (ativo e passivo);
• Peso próprio do muro;
• Peso de solo sobre o muro, na região escalonada;
• Força de atrito na base do muro.

Você pode acompanhar o cálculo de cada uma dessas forças atuantes através do vídeo abaixo:

Representando essas forças sobre o muro, temos:

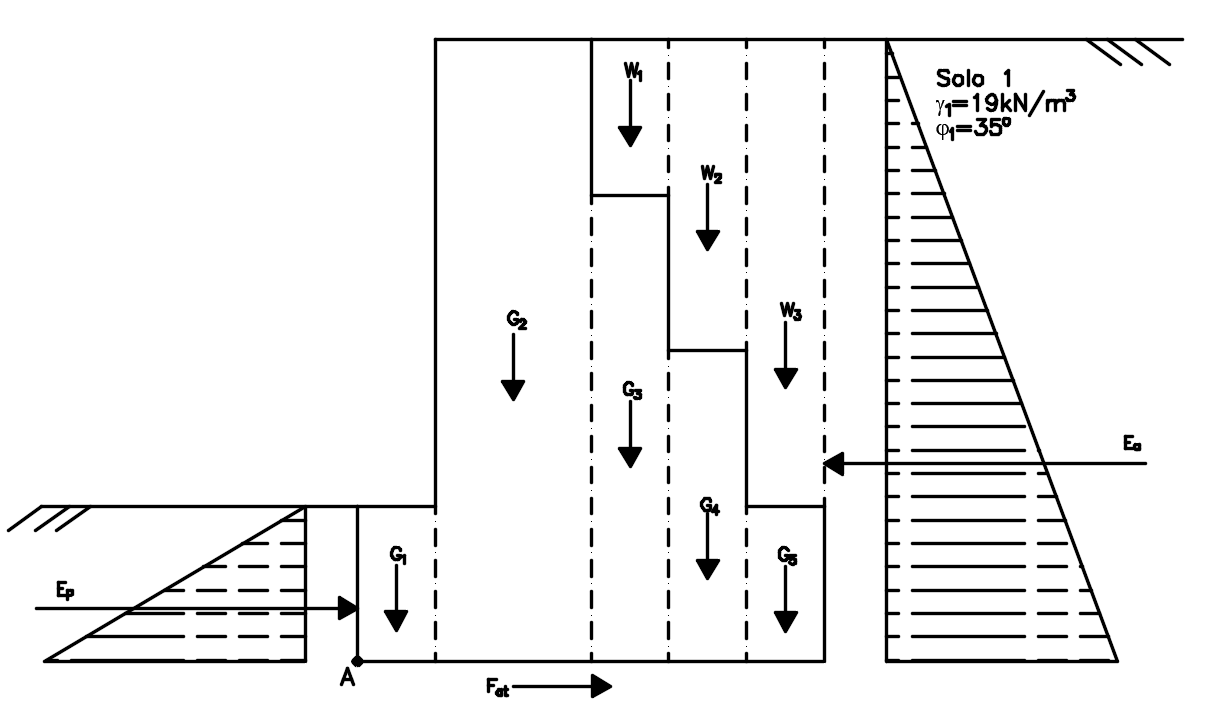
Perceba que nós separamos o peso próprio do muro, bem como o peso de solo sobre o mesmo, em várias parcelas para facilitar seu cálculo e posteriormente seus pontos de aplicações.

Como já citado no post sobre cálculo de empuxos, podemos calcular os empuxos através do volume do prisma de tensões horizontais representados na figura acima.

Para o cálculo do peso próprio, tanto de solo, quanto do muro, basta calcular o volume de material e multiplicar pelo seu peso específico.

A seguir, vamos calcular todas as ações atuantes sobre o muro para cada metro de largura do mesmo. Ou seja, para os cálculos a seguir, vamos considerar a largura de 1,0 m de muro.

Determinação dos empuxos

Vamos agora realizar o cálculo dos empuxos ativo e passivo atuantes sobre o muro de gravidade. Para tal, iniciaremos com o cálculo dos coeficientes de empuxo.

\mathrm{{k_a} = \tan^2 \left( {45 - \varphi /2} \right)}

\mathrm{{k_a} = \tan^2 \left( {45 - 35/2} \right) = 0,27}

\mathrm{{k_p} = \dfrac{1}{{{k_a}}} = 3,69}

Agora que já calculamos os valores dos coeficientes de empuxo, conseguimos calcular as tensões horizontais, e por consequência, os empuxos atuantes no muro.

Então, as tensões horizontais ativa e passiva de na base do muro são:

\mathrm{{\sigma _{ha}} = \gamma \cdot h \cdot {k_a} = 19 \cdot 4 \cdot 0,27 = 20,52kN}

\mathrm{{\sigma _{hp}} = \gamma \cdot h \cdot {k_p} = 19 \cdot 1 \cdot 3,69 = 70,11kN}

Por fim, determinaremos o empuxo ativo e passivo e seus pontos de aplicação no muro, que são o centroide dos respectivos prismas de tensões.

\mathrm{{E_a} = \dfrac{{h \cdot {\sigma _{ha}}}}{2} = \dfrac{{4 \cdot 20,52}}{2} = 41,04kN}

\mathrm{{E_p} = \dfrac{{h \cdot {\sigma _{hp}}}}{2} = \dfrac{{1 \cdot 70,11}}{2} = 35,06kN}

\mathrm{{y_a} = \dfrac{h}{3} = \dfrac{4}{3} = 1,33m}

\mathrm{{y_p} = \dfrac{h}{3} = \dfrac{1}{3} = 0,33m}

Lembrando que tais cotas de aplicação de carga estão sendo calculados em relação ao ponto A, na base do muro (vide figura acima), que é o ponto de verificação de tombamento da estrutura.

Cálculos dos pesos próprios

Para o cálculo dos pesos próprios, do muro e do solo acima do muro, como mostrado na figura acima, separamos em várias parcelas. Vamos calcular cada uma, com seu respectivo ponto de aplicação em relação ao ponto A, e por fim, determinar o peso total e seu ponto de aplicação.

\mathrm{{G_1} = 0,5 \cdot 1 \cdot 25 = 12,5kN}

\mathrm{{x_{G1}} = 0,25m}

\mathrm{{G_2} = 1 \cdot 4 \cdot 25 = 100kN}

\mathrm{{x_{G2}} = 1,0m}

\mathrm{{G_3} = 0,5 \cdot 3 \cdot 25 = 37,5kN}

\mathrm{{x_{G3}} = 1,75m}

\mathrm{{G_4} = 0,5 \cdot 2 \cdot 25 = 25kN}

\mathrm{{x_{G4}} = 2,25m}

\mathrm{{G_5} = 0,5 \cdot 1 \cdot 25 = 12,5kN}

\mathrm{{x_{G5}} = 2,75m}

Agora que já sabemos todas as parcelas do peso próprio do muro, sabemos que o peso total é a soma de todas as parcelas e que o ponto de aplicação do peso total, poderá ser calculado segundo conceitos de mecânica, através da seguinte formulação:

\mathrm{{G_T} = \sum {{G_i} = 187,5kN} }

\mathrm{{x_{GT}} = \dfrac{{\sum {{G_i} \cdot {x_i}} }}{{{G_T}}}}

\mathrm{{x_{GT}} = 1,38m}

Para o cálculo do peso de solo acima do muro, utilizaremos o mesmo raciocínio, logo temos:

\mathrm{{W_1} = 0,5 \cdot 1 \cdot 19 = 9,5kN}

\mathrm{{x_{W1}} = 1,75m}

\mathrm{{W_2} = 0,5 \cdot 2 \cdot 19 = 19kN}

\mathrm{{x_{W2}} = 2,25m}

\mathrm{{W_3} = 0,5 \cdot 3 \cdot 19 = 28,5kN}

\mathrm{{x_{W3}} = 2,75m}

\mathrm{{W_T} = \sum {{W_i} = 57kN} }

\mathrm{{x_{WT}} = \dfrac{{\sum {{W_i}} \cdot {x_i}}}{{{W_T}}} = 2,42m}

Agora que já calculamos todas as forças atuantes sobre o muro de gravidade, vamos para as verificações de deslizamento, tombamento e capacidade de carga do solo.

Tais verificações podem ser acompanhadas também através do vídeo a seguir:

Verificação ao deslizamento

Analisando as forças atuantes no muro de gravidade que estamos dimensionando, temos o seguinte esquema:

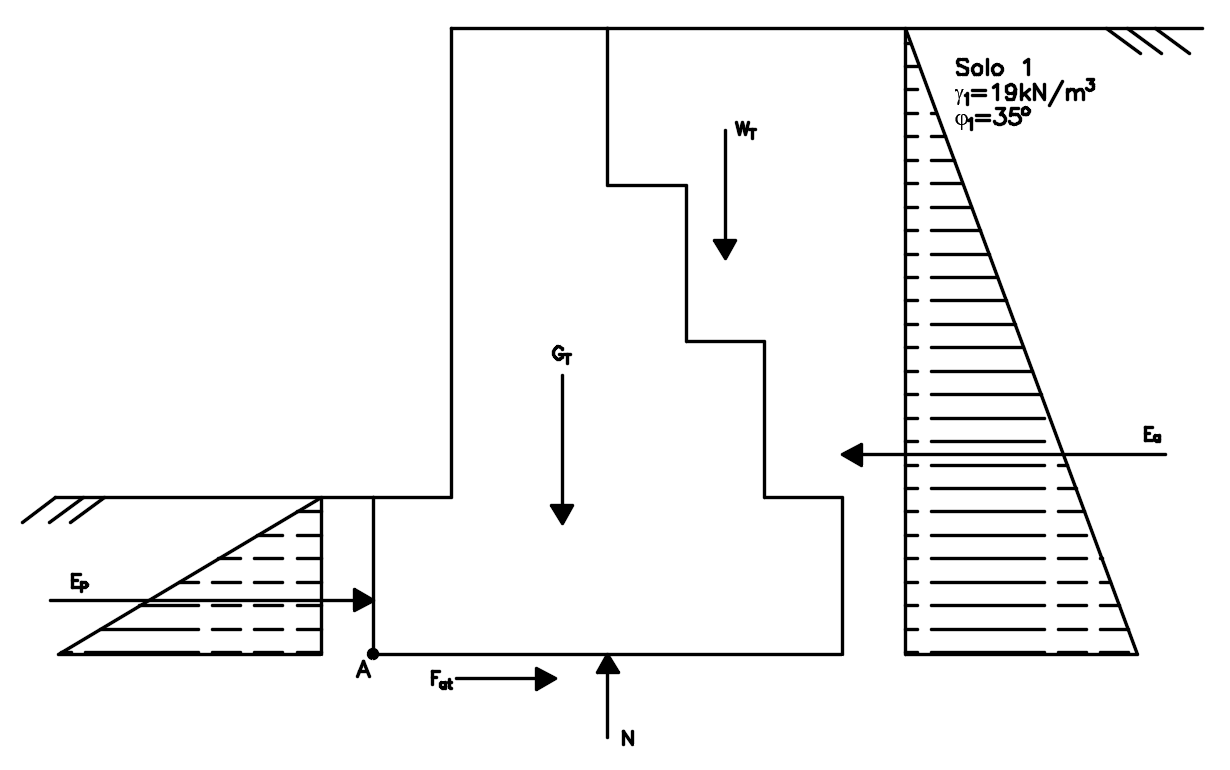
Para a verificação de deslizamento, temos que:

\mathrm{FS = \dfrac{{{F_R}}}{{{F_D}}} = \dfrac{{{E_p} + {F_{at}}}}{{{E_a}}} \ge 1,5 }

Por equilíbrio de forças verticais, podemos deduzir:

\mathrm{N = {G_T} + {W_T}}

Logo:

\mathrm{{F_{at}} = N \cdot \mu = (187,5 + 57) \cdot 0,4 = 97,8kN}

Temos, portanto, que:

\mathrm{FS = \dfrac{{35,06 + 97,8}}{{41,04}} = 3,24 \ge 1,5}

Ou seja, podemos garantir que nosso muro de gravidade está seguro quanto ao deslizamento.

Perceba também que como o fator de segurança é muito maior do que 1,5, poderíamos também voltar à etapa de pré-dimensionamento e propor um muro menos robusto, mas como estamos realizando um estudo acadêmico, vamos continuar com as próximas verificações.

Verificação ao tombamento

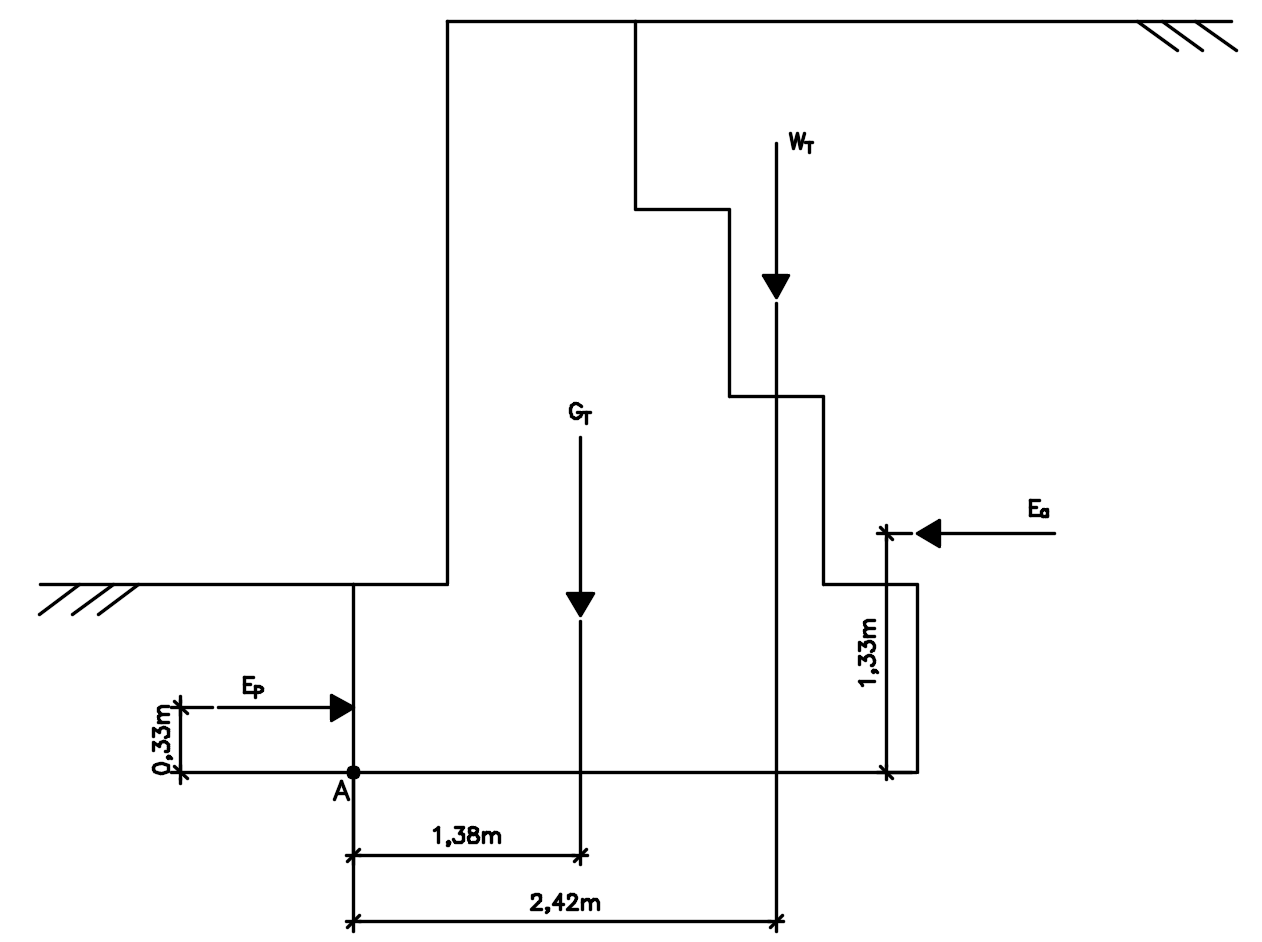
A seguir, vamos apresentar as forças já calculadas com seus pontos de aplicação, e calcular os momentos em relação ao ponto de tombamento A.

Percebemos que os momentos causados pelo peso próprio do muro, pelo peso do solo e pelo empuxo passivo tendem a estabilizar o muro. Já o momento ocasionado empuxo ativo tende a tombar o muro de gravidade. Temos então que os momentos resistente e tombante são:

\mathrm{{M_T} = {E_a} \cdot 1,33 = 54,58kN.m}

\mathrm{{M_R} = {E_p} \cdot 0,33 + G_{T} \cdot 1,38 + {W_T} \cdot 2,42}

\mathrm{{M_R} = 408,26kN.m}

Logo, o fator de segurança ao tombamento, será:

\mathrm{FS = \dfrac{{{M_R}}}{{{M_T}}} = \dfrac{{408,26}}{{54,58}} = 7,48 \ge 1,5}

Podemos garantir também a segurança do muro quanto ao tombamento!

Agora, basta verificarmos a capacidade de carga no solo, na região da base do muro de gravidade.

Verificação da capacidade de carga da base

Para a verificação da capacidade de carga da base do muro de gravidade, devemos analisar os momentos e as forças de compressão que atuam na base do muro de gravidade, sempre em relação ao centro de gravidade dessa base.

Vamos então, considerar o ponto C, na figura abaixo, como o centro da base, ou seja, se encontra a 1,5m do ponto A, já demarcado anteriormente.

Temos então que as forças e momentos atuando na base do muro são:

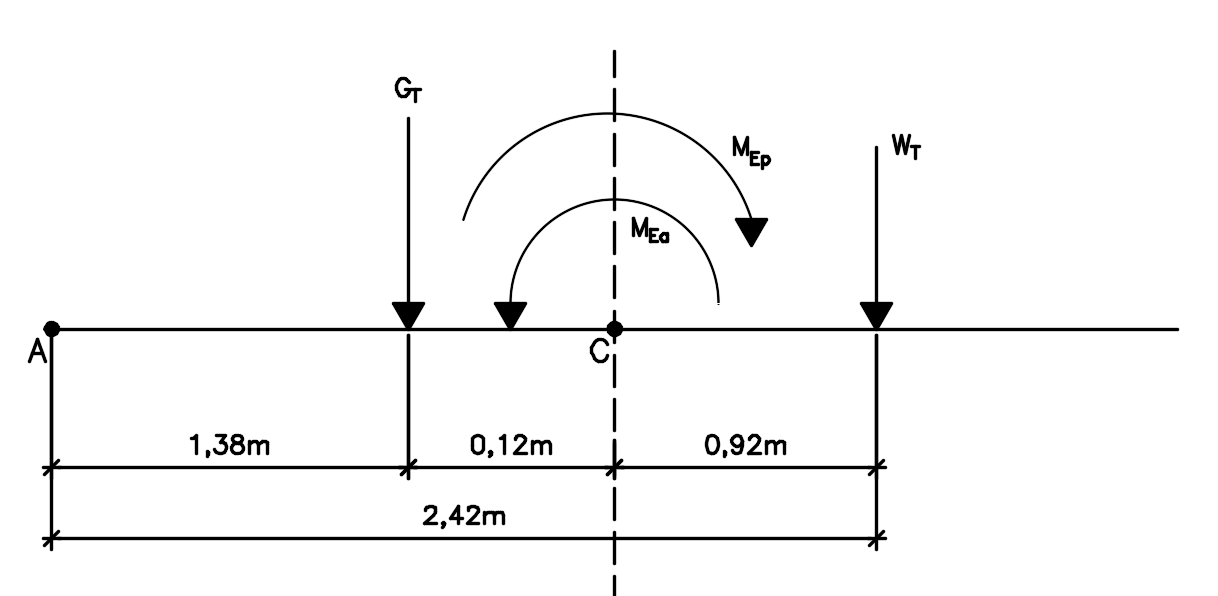
Ao levarmos as forças verticais ao centro da base (ponto C), devemos levar também seus respectivos momentos eu relação a esse ponto, temos então que os momentos de G_T e W_T em relação ao ponto C, são:

\mathrm{{M_{GT}} = {G_T} \cdot 0,12 = 22,5kN.m}

\mathrm{{M_{WT}} = - {W_T} \cdot 0,92 = 52,44kN.m}

Perceba que estamos utilizando o sinal de negativo para o momento ocasionado por W_T por convenção de momentos negativos tem sentido anti-horário, ou seja, agora temos a seguinte configuração:

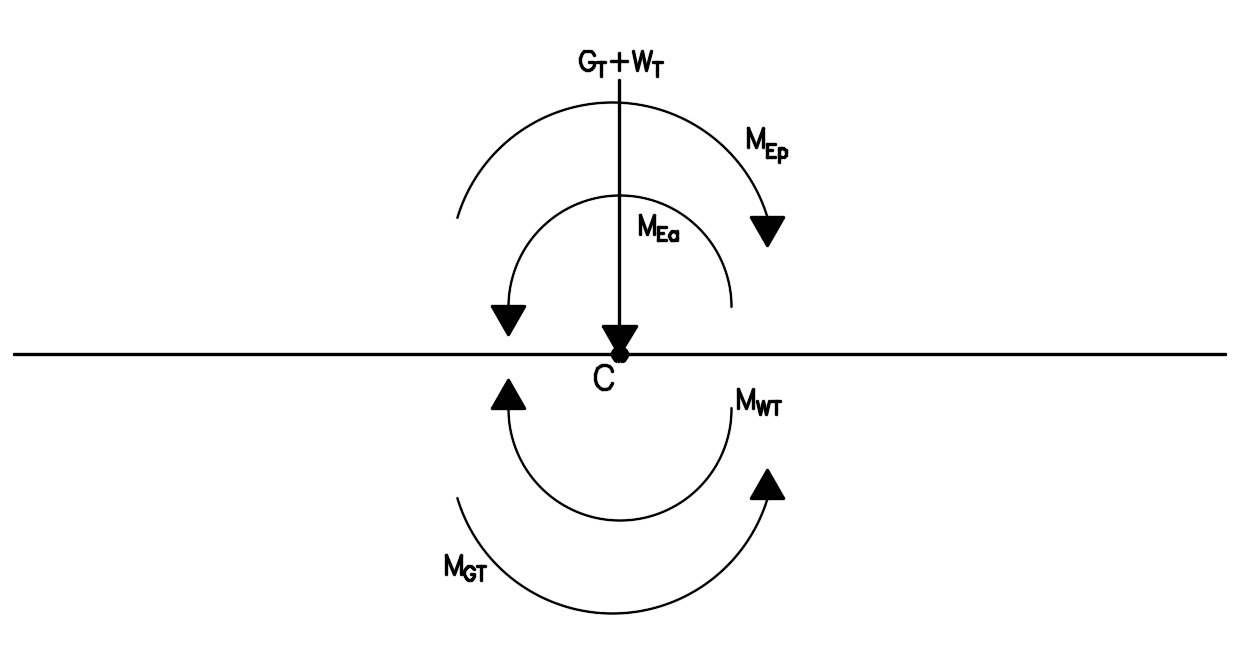
Então, calculando o momento resultante do ponto C:

\mathrm{{M_C} = {M_{Ea}} + {M_{GT}} - {M_{Ep}} - {M_{WT}}}

\mathrm{{M_C} = 54,58 + 22,5 - 11,57 - 52,44 = 13,07kN.m}

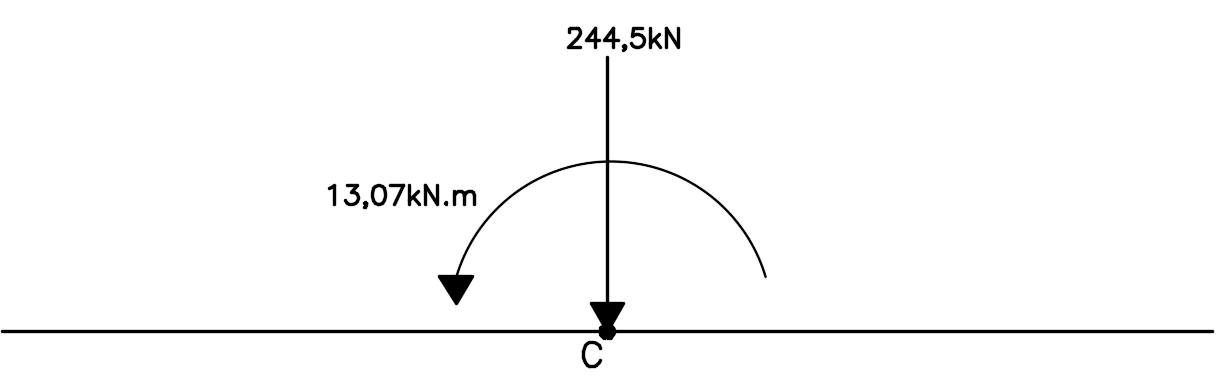
Agora que já temos a carga concentrada no centro da base e o momento resultante nesse ponto, podemos utilizar da formulação apresentada no post anterior para determinar as tensões máxima e mínima.

\mathrm{{\sigma _{máx}} = \dfrac{N}{A} + \dfrac{{6 \cdot M}}{{b}}}

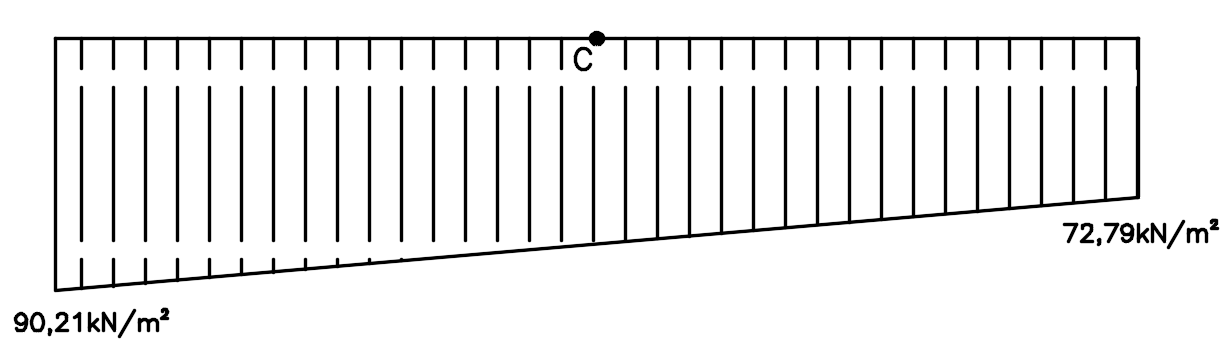
\mathrm{{\sigma _{máx}} = \dfrac{{244,5}}{{3 \cdot 1}} + \dfrac{{6 \cdot 13,07}}{9} = 90,21kN/m}

\mathrm{{\sigma _{mín}} = \dfrac{N}{A} - \dfrac{{6 \cdot M}}{{b}}}

\mathrm{{\sigma _{mín}} = \dfrac{{244,5}}{{3 \cdot 1}} - \dfrac{{6 \cdot 13,07}}{9} = 72,79kN/m}

Podemos perceber então que a tensão máxima é menor do que a tensão admissível do solo \mathrm{{\sigma _{adm}} = 150kN/m}, ou seja, podemos garantir também a estabilidade do muro quanto à capacidade de carga do solo na região da base.

Além disso, podemos perceber, visto que não ocorreram tensões negativas ao longo da base, que o solo está sofrendo compressão em toda a fundação do muro, o que é o indicado.

Pronto! Fizemos o dimensionamento e s verificações de estabilidade para um muro de gravidade. Eu disse que não seria complicado. Espero que você tenha entendido tudo!

Mas caso você ainda tenha alguma dúvida, deixa nos comentários que a gente responde!

Não deixe de seguir nosso blog, assinar nossa newsletter, além de acompanhar nosso canal no Youtube e ficar por dentro das novidades!

Até a próxima!