O caminho natural para a aprendizagem sobre o dimensionamento de sapatas submetidas a cargas excêntricas em uma direção é que você já saiba como obter as dimensões e como dimensionar a área de aço de sapatas submetidas a cargas centradas, uma vez que os procedimentos serão bem similares.
Antes de entrar nesse post eu recomendo que você percorra o caminho apresentado acima. Após isso, entraremos no dimensionamento da área de aço necessária para sapatas submetidas à cargas excêntricas em uma direção.
Método CEB-70 para sapatas
Nós utilizaremos o mesmo método utilizado para sapatas sob cargas centradas, que é o método de flexão encontrado na norma CEB-70.
Condição de aplicação do método
Apenas para relembrarmos, vou apresentar novamente a condição para aplicação do método da CEB-70.
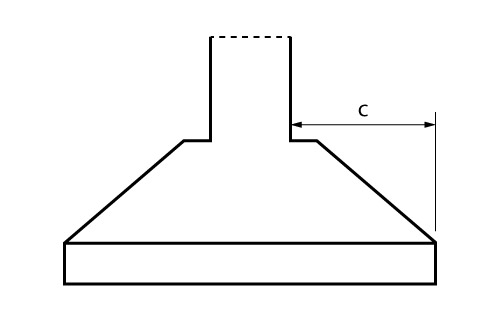
Conforme proposto na norma, para aplicação desta formulação em sapatas, as mesmas devem apresentar a seguinte condição geométrica:
\mathrm{\dfrac{h}{2} \leq c \leq 2 \cdot h }
Conceitos do método
Agora sim podemos conferir o entendimento do método para o cálculo de sapatas de concreto armado.
Esse método consiste em analisar a sapata como uma viga em balanço. Dessa forma, essa viga estaria submetida a um carregamento vertical de baixo para cima referente a reação do solo, decorrente dos esforços solicitantes, na sapata.
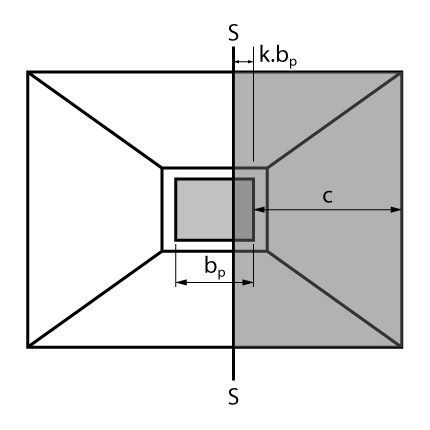
Como apresentado na figura acima, a seção S-S utilizada para dimensionamento passa a uma distância \mathrm{x = c + k \cdot b_p} da face da sapata.
Onde \mathrm{c}, vale o balanço (ou aba) da sapata naquela direção e como comentado em publicações anteriores vale:
\mathrm{c = \dfrac{B-b_p}{2}}
O \mathrm{b_p} vale a dimensão do pilar naquela direção e o \mathrm{k} vale o percentual da dimensão do pilar que a seção de dimensionamento irá avançar na direção do pilar.
O valor de \mathrm{k} varia de acordo com a literatura pesquisada, mas comumente utiliza-se \mathrm{k=0,15}. Assim sendo, podemos calcula o comprimento da viga em balanço a partir da equação abaixo:
\mathrm{x = \dfrac{B - b_p}{2} + 0,15 \cdot b_p}
Cálculo da reação na base das sapatas
Como temos agora sapatas submetidas a cargas excêntricas em uma direção, é interessante observarmos dois pontos:
- a tensão na base da sapata não será igual em todos os pontos da mesma;
- existe a possibilidade da tração ocasionada pelo momento fletor ser superior a compressão ocasionada pela carga axial.
Conforme exposto pelo trecho abaixo da norma ABNT NBR: 6122 (2019), temos que garantir o equilíbrio da seção considerando o solo como um elemento não resistente à tração.
Dessa forma, vamos dividir o dimensionamento de sapatas sob cargas excêntricas em duas situações:
a) \mathrm{e \leq \dfrac{A}{6}}, em que toda a base da sapata estará comprimida
b) \mathrm{e > \dfrac{A}{6}}
Onde \mathrm{e} vale a excentricidade da carga aplicada e pode ser calculada por \mathrm{e=\dfrac{M}{N}} e \mathrm{A} é a dimensão da sapata na direção da carga excêntrica.
É interessante lembrarmos de onde vem esse limite de \mathrm{\dfrac{A}{6}}. O mesmo tem origem do conceito de núcleo central de inércia, de Resistência dos Materiais, em que uma força de compressão localizada dentro do mesmo não provará tensões de tração na seção.
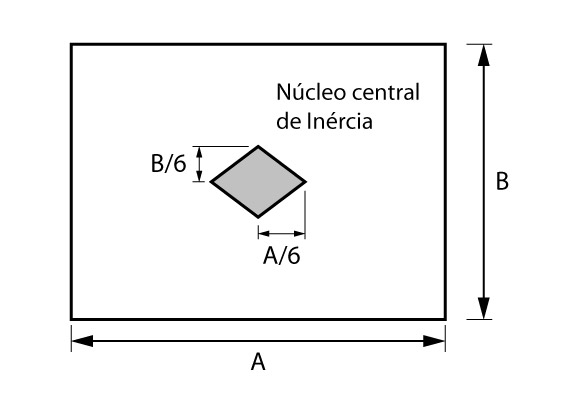
Caso \mathrm{e \leq \dfrac{A}{6}}
Para essa situação, toda a base da sapata estará comprimida. Dessa forma, as tensões podem ser obtidas diretamente por resistência dos materiais, apenas somando a tensão oriunda da força axial e a tensão ocasionada pelo momento fletor:
\mathrm{\sigma = \dfrac{N}{A \cdot B} + \dfrac{M \cdot x}{I}}
Considerando a força excêntrica na direção x, teremos a inercia como:
\mathrm{I = \dfrac{B \cdot A^3}{12}}
Realizando a substituição \mathrm{M = N \cdot e}, teremos a seguinte formulação:
\mathrm{\sigma = \dfrac{N}{A \cdot B} + \dfrac{N \cdot e \cdot \dfrac{A}{2}}{\dfrac{B \cdot A^3}{12}}}
\mathrm{\sigma_{max} = \dfrac{N}{A \cdot B} \cdot \left( 1 + \dfrac{6 \cdot e}{A} \right)}
Essa formulação nos dará a reação do solo por unidade de área, que será utilizada para o dimensionamento da armação.
No outro lado da sapata, a tensão mínima pode ser calculada de forma análoga, apenas trocando o sinal da fórmula:
\mathrm{\sigma_{min} = \dfrac{N}{A \cdot B} \cdot \left( 1 - \dfrac{6 \cdot e}{A} \right)}
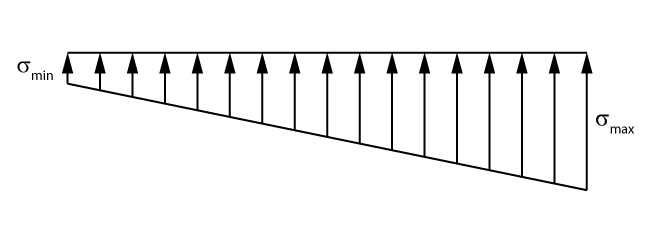
Caso \mathrm{e > \dfrac{A}{6}}
Agora com a força aplicada fora do núcleo central de inércia, parte da base da sapata estaria sob tensões de tração. Assim sendo, deve ser realizado um novo diagrama, em que a parte tracionada é excluída.
O primeiro passo é garantir que a resultante da reação coincida com a posição da carga aplicada:
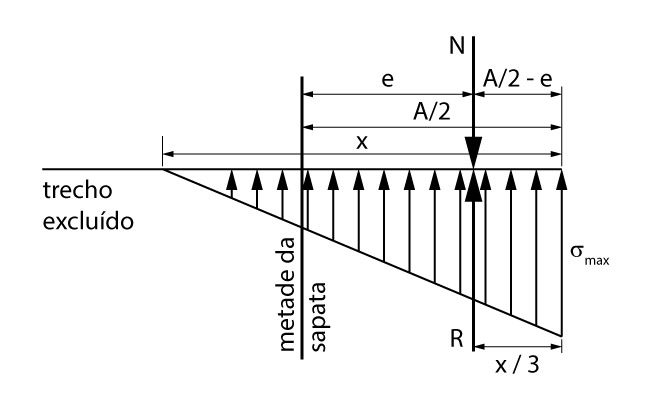
Pela figura acima, podemos constatar geometricamente que a força normal está aplicada a uma distância \mathrm{\left( \dfrac{A}{2} - e \right)} da extremidade mais comprimida. Considerando \mathrm{x} a base do triangulo de tensões, ou seja, o valor do trecho comprimido e sabendo que o baricentro do triangulo se encontra a 1/3 do ângulo reto, temos que:
\mathrm{\dfrac{x}{3} = \dfrac{A}{2} - e}
Assim sendo, o comprimento do trecho comprimido vale:
\mathrm{x = 3 \cdot \left( \dfrac{A}{2} - e \right)}
O próximo passo é garantir que a resultante da força de reação seja igual a normal aplicada.
Como \mathrm{\sigma_max} se refere a uma tensão, vamos multiplicar esse valor pela outra dimensão da sapata (\mathrm{B}) a fim de obter um carregamento distribuído.
Agora basta calcularmos a área do triangulo para obtermos a força total de reação do solo:
\mathrm{\dfrac{\sigma_{max} \cdot B \cdot x}{2} = N}
\mathrm{\dfrac{\sigma_{max} \cdot B \cdot 3 \cdot \left( \dfrac{A}{2} - 2 \right)}{2} = N}
Assim, a tensão máxima na base da sapata será:
\mathrm{\sigma_{max} = \dfrac{2 \cdot N}{3 \cdot B \cdot \left( \dfrac{A}{2} - e \right)}}

Trecho comprimido mínimo
Para situações em que a carga se encontra fora do núcleo central de inércia, ou seja, parte da base da sapata não está comprimida, a norma limita o percentual mínimo de zona comprimida:
Como sabemos que o trecho comprimido vale \mathrm{x}, podemos colocar que:
\mathrm{x \geq \dfrac{2}{3} \cdot A}
\mathrm{3 \cdot \left( \dfrac{A}{2} - e \right) \geq \dfrac{2}{3} \cdot A}
\mathrm{e \leq \dfrac{5 \cdot A}{18}}
Obtenção do momento solicitante nas sapatas
Agora que já conhecemos a distribuição de tensões na base da sapata, basta multiplicarmos a tensão por uma largura qualquer, a fim de obter uma distribuição por unidade de comprimento.
Recomendo multiplicar a reação por área por uma largura de 1,0 m. Uma vez que, com isso teremos uma carregamento linear representando uma largura de 1,0 m da sapata e consequentemente, a área de aço calculada será também obtida para cada metro.
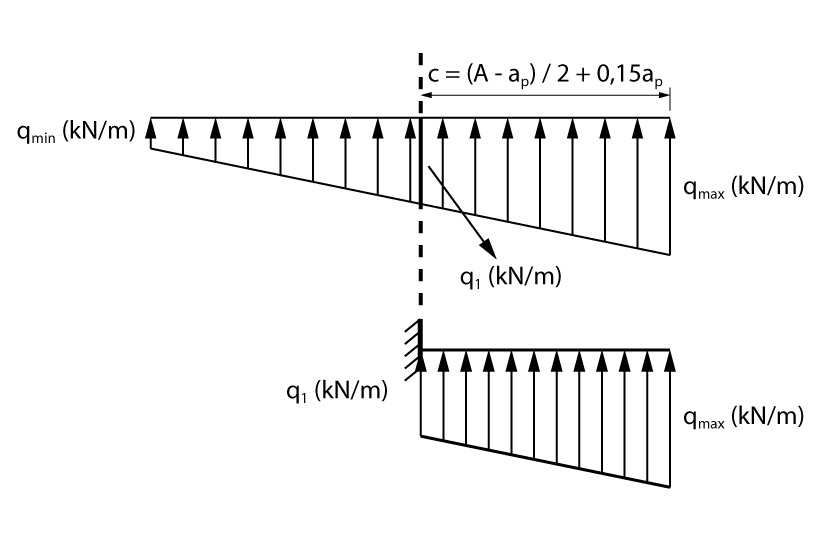
Agora que já temos o esquema de reação distribuída para a viga em balanço que representa uma seção da sapata, basta calcularmos o momento atuante na mesma (seção S-S).
Para obtenção do momento da seção do engaste, basta dividirmos o bloco trapezoidal em um bloco retangular e outro bloco triangular, conforme mostra a figura abaixo:
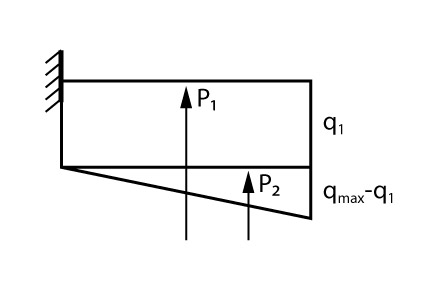
Como se trata de um retângulo e um triangulo, fica fácil calcularmos a área e o ponto de aplicação das forças resultantes. Assim podemos calcular o momento máximo:
\mathrm{ M_{máx} = q_1 \cdot c \cdot \dfrac{c}{2} + \dfrac{\left( q_max - q_1 \right) \cdot c}{2} \cdot \dfrac{2 \cdot c}{3} }
Área de aço de sapatas
É possível utilizarmos o mesmo entendimento utilizado para o dimensionamento de vigas para o dimensionamento de sapatas.
Sendo assim, a área de aço necessária será basicamente um momento atuante dividido pelo produto do braço de alavanca e tensão de escoamento do aço utilizado.
\mathrm{ As = \dfrac{M}{Z \cdot f_{yd}} }
Conforme Machado (1985) afirma, para o caso sapata com regiões inclinadas, podemos aproximar o braço de alavanca para \mathrm{z = 0,85 \cdot d}, garantindo um erro máximo de 10%.
Dessa forma, a área de aço pode ser calculada pela seguinte formulação:
\mathrm{ As = \dfrac{M_{Sd}}{0,85 \cdot d \cdot f_{yd}} }
Vale lembrar que como o momento utilizado nessa etapa foi obtido para uma faixa de 1,0 m de largura, a área de aço também equivale a uma faixa de mesma largura.
Armadura mínima para sapatas
Na literatura é possível encontrar algumas proposições para armadura mínima em sapatas.
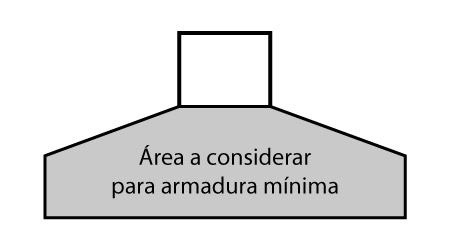
[interesse-fundacoes-rasas]Nessa publicação iremos considerar como armadura mínima como uma taxa da área de concreto da seção levando em consideração a superfície inclinada, conforme ilustra a figura abaixo.
Área para armadura mínima de sapatas
Como se trata de um trapézio somado a um retângulo, esta área pode ser calculada pela seguinte expressão:
\mathrm{ A_c = B \cdot h_0 + \dfrac{B + b_p}{2} \cdot (h - h_0) }
Analisando agora a taxa que multiplica a área de concreto, iremos utilizar o mesmo \mathrm{\rho_{min}} utilizado para vigas de concreto armado.
O valor de \mathrm{\rho_{min}} pode ser obtido na tabela abaixo, fornecida na ABNT/NBR: 6118 (2014), para cada classe de concreto.
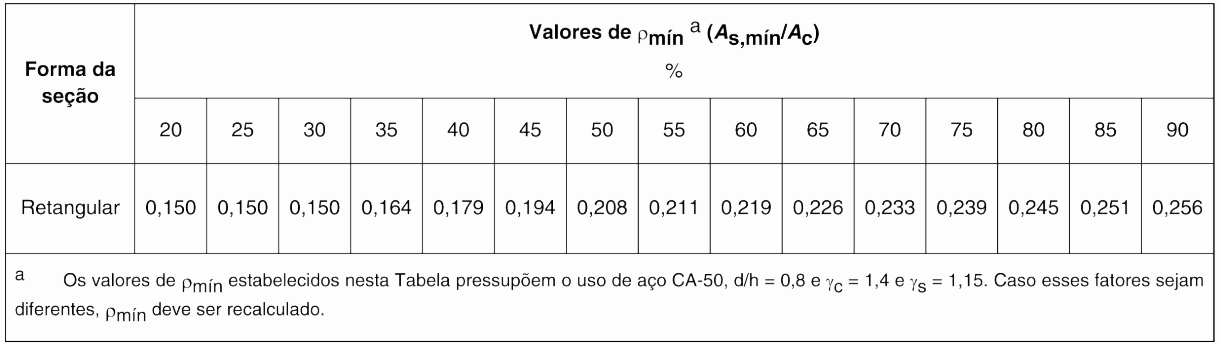
Dessa forma, o cálculo da área de aço mínima será:
\mathrm{As_{min} = \rho_{min} \cdot A_c}
É interessante que ao obtermos essa área também dividirmos a mesma pela largura da seção analisada, a fim de obter também uma área de aço por metro de largura. Com isso, poderemos comparar a mesma com a área de aço calculada
Recado final
Por fim, acredito que ao final desse leitura você tenha aprendido como dimensionar sapatas submetidas à cargas excêntricas em uma direção. Se ainda ficou com alguma dúvida ou tem sugestão para conteúdos futuros basta escrever nos comentários abaixo.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

Material muito bom. Parabéns 🙂
Muito obrigado, Fernanda!
Parabéns José Moura! Sua didática valoriza seus conhecimentos!
Vamos em frente!
Obrigado, Osmar!
Abraço!