Nessa série de posts você vai acompanhar o dimensionamento completo de um reservatório elevado na prática.
Na primeira parte vamos focar apenas na obtenção dos esforços para os dimensionamentos como placas.
Caso você desconheça a teoria sobre o dimensionamento de reservatórios elevados, eu recomendo que confira a publicação anterior.
Geometria do reservatório
Vamos analisar inicialmente a geometria de nosso reservatório. O mesmo possui as dimensões internas de 400 cm por 250 cm em vista superior e possui 210 cm internamente na direção da altura. As paredes do reservatório são apoiadas em pilares localizados nos quatro cantos.
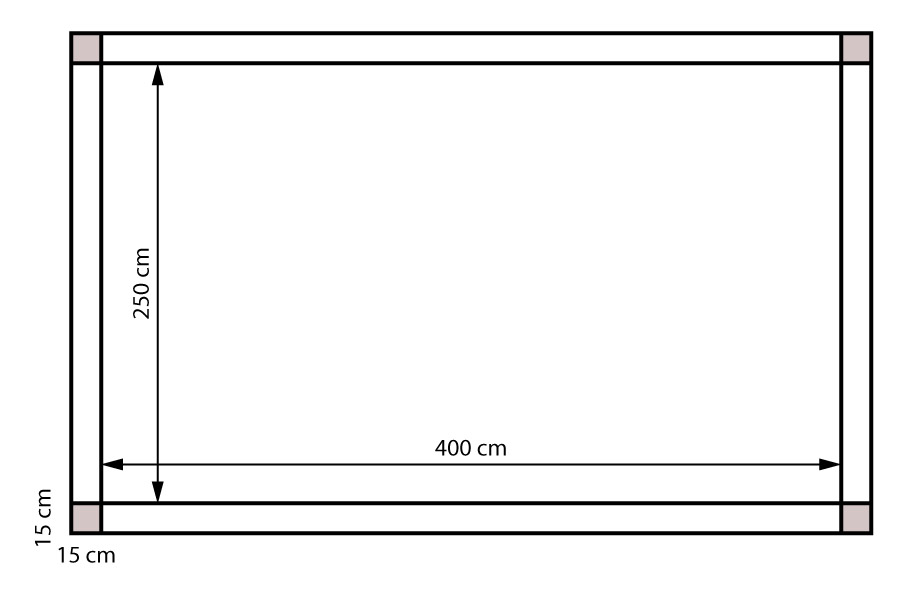
O corte abaixo indica as espessuras utilizadas para as lajes: 15 cm para a laje de fundo e para as paredes e 10 cm para a laje de tampa.
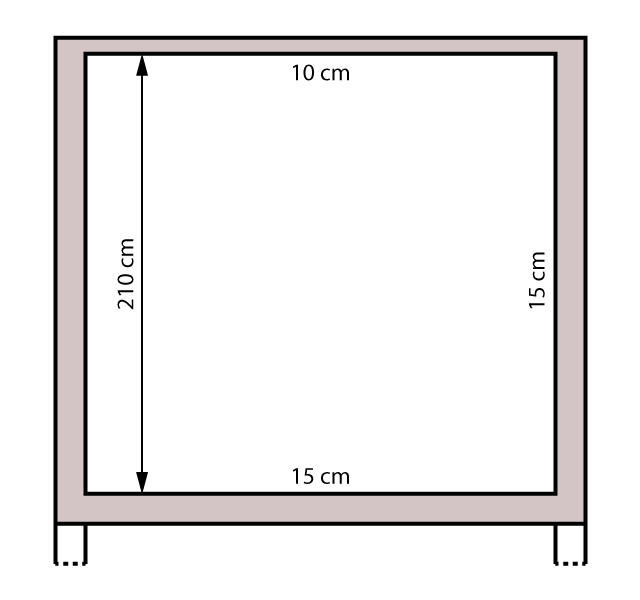
Cálculo como lajes
Como sabemos, é necessário dimensionar as paredes como as lajes de fundo e de tampa. As paredes devem ser dimensionadas tanto como laje como dimensionadas como vigas ou vigas-parede. Vamos iniciar com os dimensionamento como placas.
Obtenção dos carregamento
Vamos calcular as cargas atuantes em cada um dos elementos estudados.
Laje de tampa
Na laje de tampa temos a atuação do peso próprio, do revestimento e da sobrecarga de utilização (também denominada de carga acidental).
Calcularemos o peso próprio pela seguinte formulação:
\mathrm{0,1 \cdot 25 = 2,5 \; kN/m^2}
No revestimento e na sobrecarga de utilização utilizaremos carregamentos padrões de, respectivamente, \mathrm{1,0 \; kN/m^2} e \mathrm{0,5 \; kN/m^2}.
Dessa forma, a carga total na laje de tampa será \mathrm{4,0 \; kN/m^2}.
Laje de fundo
Já para a laje de fundo temos o peso próprio, o revestimento e o carregamento correspondente a água acima da laje.
No revestimento também utilizaremos \mathrm{1,0 \; kN/m^2}.
Para o peso próprio utilizaremos a mesma formulação mas alterando a espessura:
\mathrm{0,15 \cdot 25 = 3,75 \; kN/m^2}
Vamos calcular agora a pressão hidrostática sobre a laje de fundo:
\mathrm{10 \cdot 2,1 = 21 \; kN/m^2}
Totalizando, temos uma carga de \mathrm{25,75 \; kN/m^2} aplicada na laje de fundo.
Paredes
A única carga que atua na parede perpendicularmente ao seu plano médio é o empuxo causado pela água armazenada. O mesmo pode ser calculado pela equação abaixo:
\mathrm{10 \cdot 2,1 = 21 \; kN/m^2}
Lembre-se que esse é somente o valor máximo do empuxo, localizado no fundo do reservatório. O carregamento de empuxo será um carga triangular variando de zero, no topo do reservatório, até o valor máximo, na base do reservatório.
Esforços no reservatório
Utilizaremos nessa análise de esforços as tabelas de Czerny, que por conveniência colocarei novamente abaixo:
Laje de tampa
Conforme vimos em lajes maciças, não necessariamente temos que avançar o vão de cálculo até o eixo da viga de apoio. Podemos utilizar o menor valor entre metade da largura de apoio e 30% da espessura da laje:
\mathrm{ b \leq \left\{ \begin{array}{ll} \dfrac{15}{2} = 7,5 \; cm \\ 0,3 \cdot 10 = 3 \; cm \end{array} \right. }
Dessa forma o vão de cálculo (também denominado de vão efetivo ou teórico) será:
\mathrm{\left( 400 + 3 + 3 \right) = 406 \; cm} e \mathrm{\left( 250 + 3 + 3 \right) = 256 \; cm}
Agora sabemos que estamos atrás do esforço de uma laje simplesmente apoiada nas quatro bordas, com um carregamento distribuído de \mathrm{4,0 \; kN/m^2} e com as dimensões internas de 4,06 m e 2,56 m podemos entrar na tabela de Czerny.
Calculando a relação entre as dimensões:
\mathrm{\dfrac{l_y}{l_x} = \dfrac{4,06}{2,56} = 1,6}
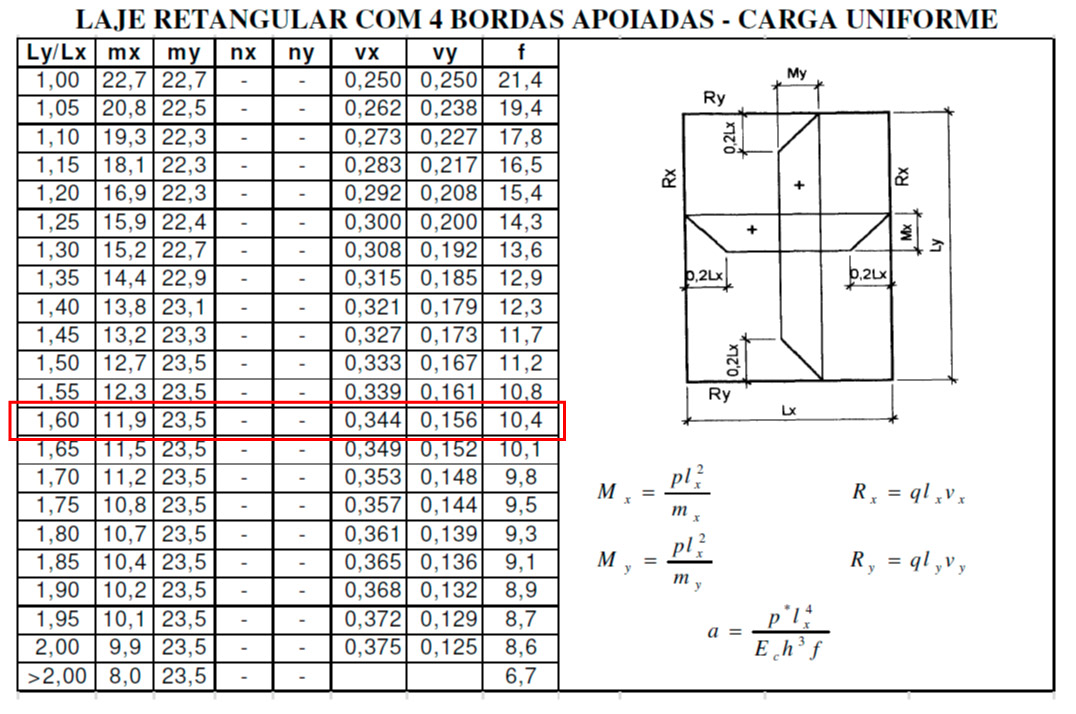
Com os valores de 11,9 e 23,5 retirados na tabela de Czerny podemos calcular os momentos nas duas direções.
Para a direção menor temos:
\mathrm{M_x = \dfrac{p \cdot l_x ^2}{m_x}}
\mathrm{M_x = \dfrac{4 \cdot 2,56 ^2}{11,9} = 2,2 \; kN \cdot m / m}
Calculando agora o momento na direção maior:
\mathrm{M_y = \dfrac{p \cdot l_x ^2}{m_y}}
\mathrm{M_x = \dfrac{4 \cdot 2,56 ^2}{23,5} = 1,12 \; kN \cdot m / m}
Para as reações de apoio nas duas direções, teremos:
\mathrm{R_x = q \cdot l_x \cdot v_x = 4 \cdot 2,56 \cdot 0,344 = 3,52 \; kN / m}
\mathrm{R_y = q \cdot l_y \cdot v_y = 4 \cdot 4,06 \cdot 0,156 = 2,53 \; kN / m}
Laje de fundo do reservatório
Vamos calcular o vão teórico também para laje de fundo da mesma maneira como calculamos a laje de tampa:
\mathrm{ b \leq \left\{ \begin{array}{ll} \dfrac{15}{2} = 7,5 \; cm \\ 0,3 \cdot 15 = 4,5 \; cm \end{array} \right. }.
Assim sendo, teremos os seguintes vãos de cálculo:
\mathrm{\left( 400 + 4,5 + 4,5 \right) = 409 \; cm} e \mathrm{\left( 250 + 4,5 + 4,5 \right) = 259 \; cm}
A pequena diferença nas dimensões da laje de tampa para laje de fundo faz com que não haja alterações na razão entre as dimensões, permanecendo assim em 1,6.
Mesmo mantendo a razão entre as duas direções igual, temos alteração tanto nas condições de contorno (agora engastada nas quatro bordas) quanto no carregamento em si.
Entrando na tabela de Czerny novamente:
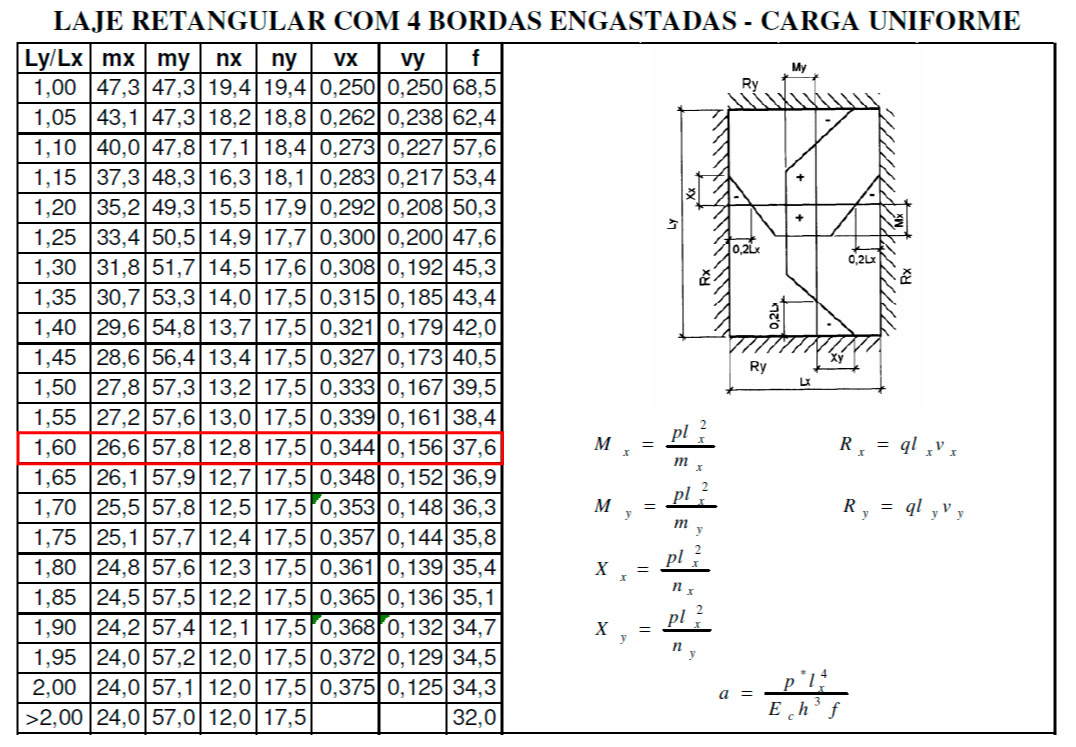
Utilizando agora os valores encontrados na tabela, teremos para menor direção:
\mathrm{M_x = \dfrac{25,75 \cdot 2,59 ^2}{26,6} = 6,49 \; kN \cdot m / m}
\mathrm{X_x = \dfrac{25,75 \cdot 2,59 ^2}{12,8} = 13,49 \; kN \cdot m / m}
Podemos calcular também os momentos para a maior dimensão:
\mathrm{M_y = \dfrac{25,75 \cdot 2,59 ^2}{57,8} = 2,99 \; kN \cdot m / m}
\mathrm{X_y = \dfrac{25,75 \cdot 2,59 ^2}{17,5} = 9,87 \; kN \cdot m / m}
As reações de apoio para as duas direções serão:
\mathrm{R_x = q \cdot l_x \cdot v_x = 25,75 \cdot 2,59 \cdot 0,344 = 22,94 \; kN / m}
\mathrm{R_y = q \cdot l_y \cdot v_y = 25,75 \cdot 4,09 \cdot 0,156 = 16,43 \; kN / m}
Paredes 1 e 2
Chamarei aqui de paredes 1 e 2 aquelas dispostas na direção horizontal na vista superior, apresentada no início dessa publicação.
Inicialmente, vamos calcular logo quanto avançaremos além do vão livre:
\mathrm{ b_1 \leq \left\{ \begin{array}{ll} \dfrac{10}{2} = 5 \; cm \\ 0,3 \cdot 15 = 4,5 \; cm \end{array} \right. = 4,5 \; cm}.
\mathrm{ b_2 \leq \left\{ \begin{array}{ll} \dfrac{15}{2} = 5 \; cm \\ 0,3 \cdot 15 = 4,5 \; cm \end{array} \right. = 4,5 \; cm}.
Os valores de \mathrm{b_1} e \mathrm{b_2}, representam o quanto deveremos avançar em direção, respectivamente, da laje de topo e da laje de fundo e paredes.
Assim sendo, os vãos efetivos para as paredes 1 e 2 são:
\mathrm{\left( 400 + 4,5 + 4,5 \right) = 409 \; cm} e \mathrm{\left( 210 + 4,5 + 4,5 \right) = 219 \; cm}
Vamos entrar na tabela de Czerny para um carregamento triangular e para uma laje simplesmente apoiada em uma borda e engastada nas outras três com relação entre as dimensões:
\mathrm{\dfrac{l_y}{l_x} = \dfrac{4,09}{2,19} = 1,87 \rightarrow 2,00}
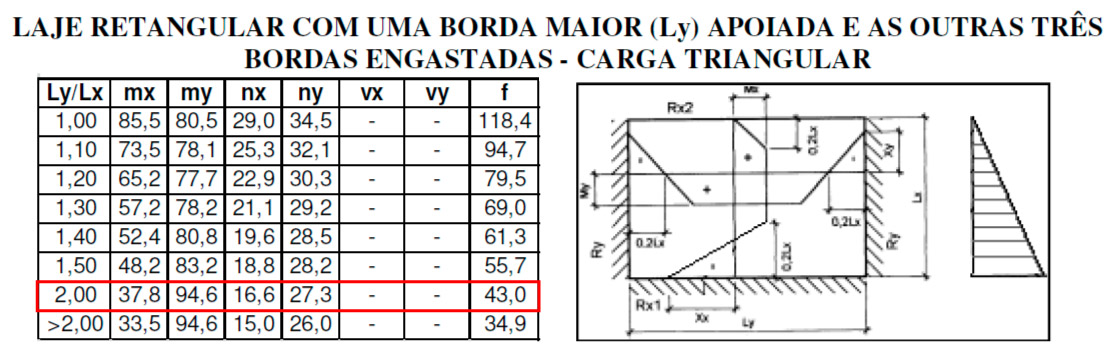
Assim, podemos calcular os esforços nas duas direções. Iniciando pela menor direção, temos:
\mathrm{M_x = \dfrac{21 \cdot 2,19 ^2}{37,8} = 2,66 \; kN \cdot m / m}
\mathrm{X_x = \dfrac{21 \cdot 2,19 ^2}{16,6 }= 6,06 \; kN \cdot m / m}
Agora na maior direção:
\mathrm{M_y = \dfrac{21 \cdot 2,19 ^2}{94,6} = 1,06 \; kN \cdot m / m}
\mathrm{X_y = \dfrac{21 \cdot 2,19 ^2}{27,3} = 3,69 \; kN \cdot m / m}
Como a tabela de Czerny não fornece as reações de apoio para o caso de carga triangular, utilizaremos aqui as mesmas condições de contorno mas com um carregamento médio, ou seja, \mathrm{10,5 \; kN \; m^2}.
Assim sendo, teremos:
\mathrm{R_{x1} = q \cdot l_x \cdot v_{x1} = 21 \cdot 2,19\cdot 0,437 = 19,18 \; kN / m}
\mathrm{R_{x2} = q \cdot l_x \cdot v_{x2} = 21 \cdot 2,19 \cdot 0,245 = 10,75 \; kN / m}
\mathrm{R_y = q \cdot l_y \cdot v_y = 21 \cdot 4,09 \cdot 0,159 = 13,66 \; kN / m}
Paredes 3 e 4
De forma similar ao que fizemos com as paredes 1 e 2, os vãos efetivos das paredes 3 e 4 serão:
\mathrm{\left( 250 + 4,5 + 4,5 \right) = 259 \; cm} e \mathrm{\left( 210 + 4,5 + 4,5 \right) = 219 \; cm}
Com a relação \mathrm{\dfrac{l_y}{l_x} = \dfrac{2,59}{2,19} = 1,18 \rightarrow 1,20} podemos obtemos nossos esforços:
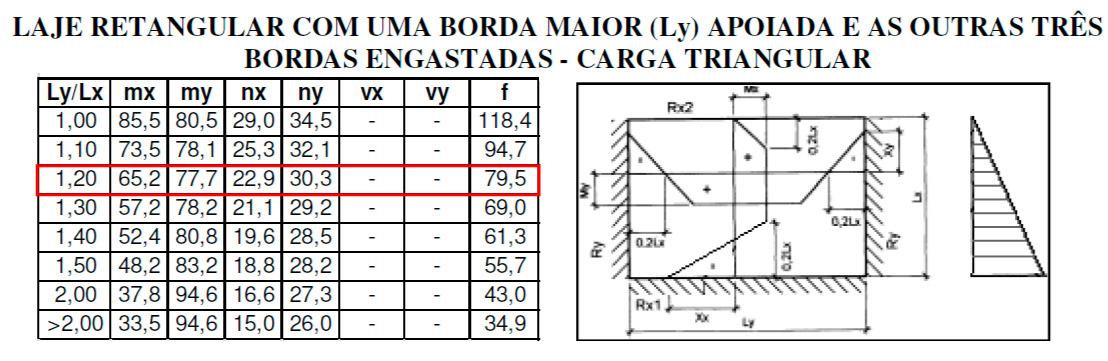
Assim, podemos calcular os esforços nas duas direções. Iniciando pela menor direção, temos:
\mathrm{M_x = \dfrac{21 \cdot 2,19 ^2}{65,2} = 1,54 \; kN \cdot m / m}
\mathrm{X_x = \dfrac{21 \cdot 2,19 ^2}{22,9} = 4,40 \; kN \cdot m / m}
Agora na maior direção:
\mathrm{M_y = \dfrac{21 \cdot 2,19 ^2}{77,7} = 1,30 \; kN \cdot m / m}
\mathrm{X_y = \dfrac{21 \cdot 2,19 ^2}{30,3} = 3,32 \; kN \cdot m / m}
Conforme realizado nas outras paredes, também utilizaremos aqui um carregamento médio de \mathrm{10,5 \; kN \; m^2}.
Assim sendo, teremos:
\mathrm{R_{x1} = q \cdot l_x \cdot v_{x1} = 21 \cdot 2,19\cdot 0,301 = 13,84 \; kN / m}
\mathrm{R_{x2} = q \cdot l_x \cdot v_{x2} = 21 \cdot 2,19 \cdot 0,171 = 7,86 \; kN / m}
\mathrm{R_y = q \cdot l_y \cdot v_y = 21 \cdot 2,59 \cdot 0,264 = 14,36 \; kN / m}
Resumo dos esforços calculados antes da compatibilização
A imagem abaixo resume todos os esforços encontrados em nosso reservatório.
Nessa representação, a direção do esforço indicado é representada pela rotação do texto. Além disso, as linhas mais espessas representam a condição de engastamento.
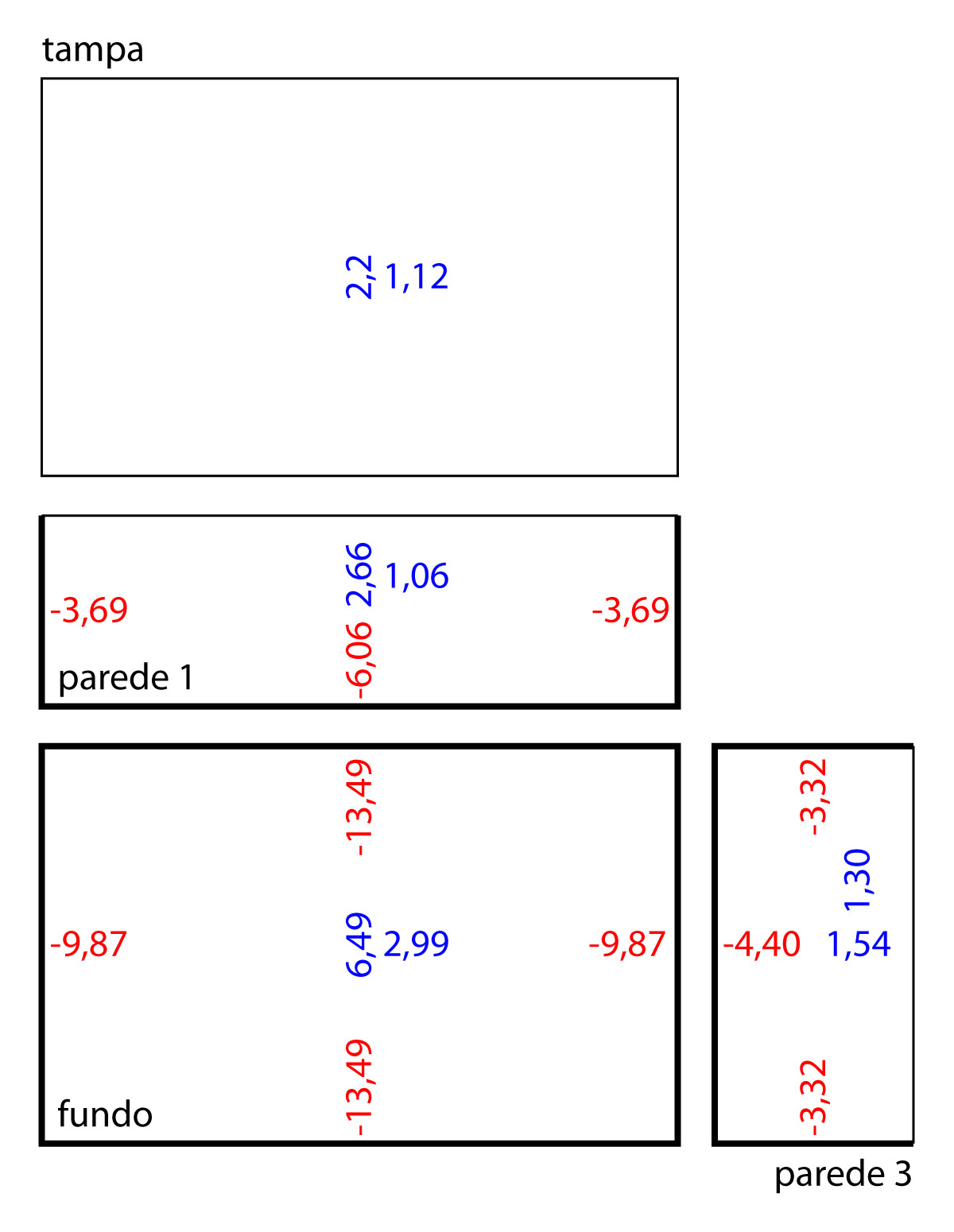
Compatibilização dos momentos
Vamos agora iniciar a etapa de compatibilização dos momentos entre os elementos isolados. Vale lembrar que além ajustarmos o momento negativo nos encontros devem ser corrigidos os momentos positivos.
Laje de fundo e parede 1
Utilizaremos o maior valor entre a média dos momentos e 80% do maior dos momentos para obter o momento negativo compatibilizado:
\mathrm{ X_x ^* \geq \left\{ \begin{array}{ll} \dfrac{13,49+6,06}{2} = 9,78 \; kN \cdot m /m \\ 0,8 \cdot 13,49 = 10,79 \; kN \cdot m /m \end{array} \right. = 10,79 \; kN \cdot m /m}
Corrigindo agora o momento positivo na laje de fundo:
\mathrm{M_x ^* = 6,49 + \dfrac{13,49-10,79}{2} + \dfrac{13,49-10,79}{2} = 9,19 \; kN \cdot m /m }
Laje de fundo e parede 3
Partindo das mesmas condições apresentadas anteriormente, temos o momento negativo compatibilizado:
\mathrm{ X_y ^* \geq \left\{ \begin{array}{ll} \dfrac{9,87+4,40}{2} = 7,14 \; kN \cdot m /m \\ 0,8 \cdot 9,87 = 7,90 \; kN \cdot m /m \end{array} \right. = 7,90 \; kN \cdot m /m}
Alterando agora o momento positivo para outra direção da laje do fundo:
\mathrm{M_y ^* = 2,99 + \dfrac{9,87-7,90}{2} + \dfrac{9,87-7,90}{2} = 4,96 \; kN \cdot m /m }
Parede 1 e parede 3
Vamos compatibilizar inicialmente o momento negativo:
\mathrm{ X_y ^* \geq \left\{ \begin{array}{ll} \dfrac{3,69+3,32}{2} = 3,51 \; kN \cdot m /m \\ 0,8 \cdot 3,69 = 2,95 \; kN \cdot m /m \end{array} \right. = 3,51 \; kN \cdot m /m}
E então vamos corrigir o momento positivo na parede 1:
\mathrm{M_y ^* = 1,06 + \dfrac{3,69-3,51}{2} + \dfrac{3,69-3,51}{2} = 1,24 \; kN \cdot m /m }
Resumo dos esforços após a compatibilização
Após a compatibilização nós teremos a imagem apresentada acima mas resumindo os esforços já ajustados. Preferi dar um destaque na representação para os esforços que sofreram alteração.
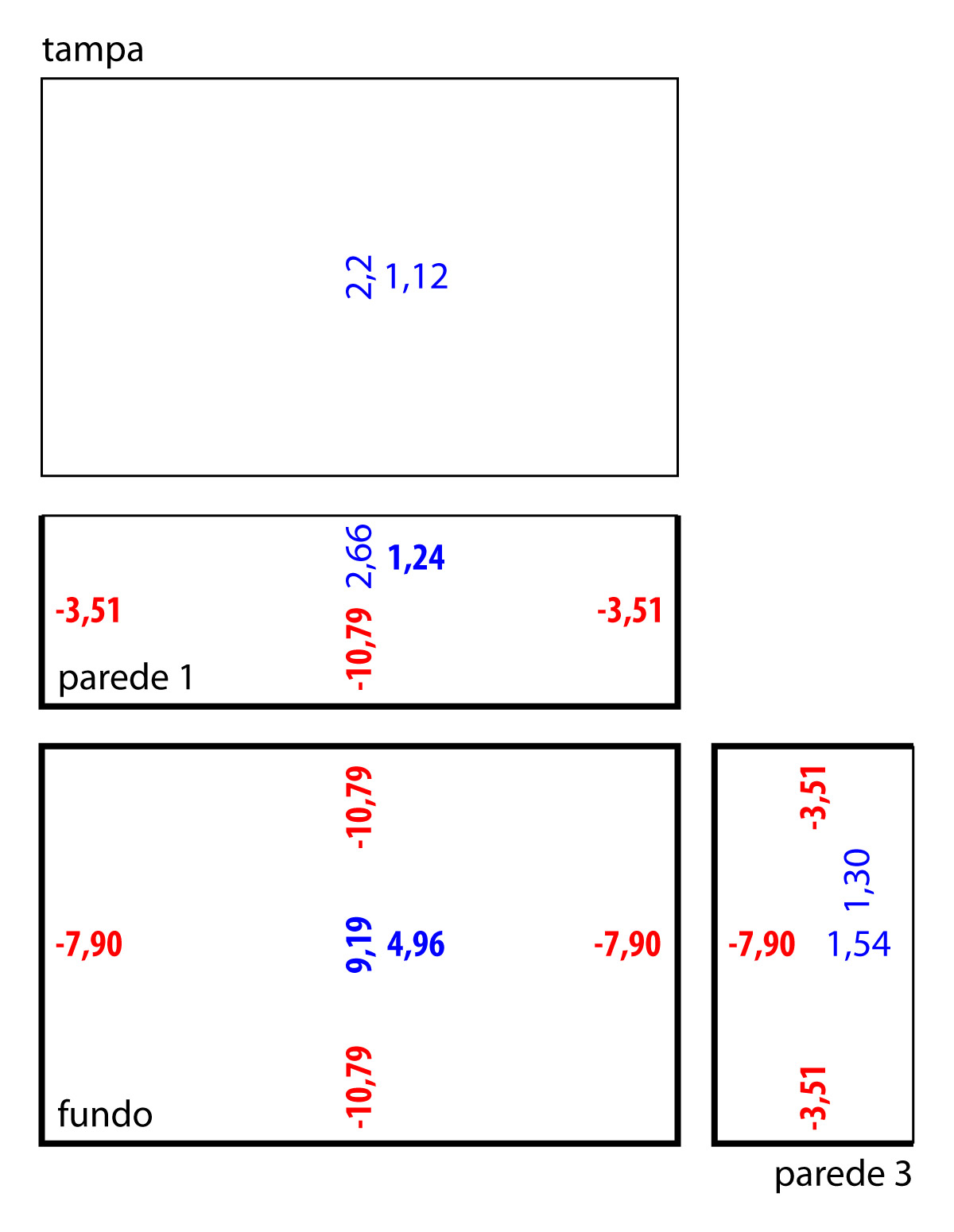
Recado final
Parabéns por ter avançado até aqui! Em breve continuaremos essa resolução entrando na parte de dimensionamento da área de aço como laje, dimensionamento como viga ou viga-parede, verificação de fissuras e detalhamento dos elementos. Não deixe de acompanhar o blog para conferir!
Caso ainda tenha sobrado alguma dúvida, não hesite em escrever nos comentários abaixo.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
