Por experiência própria eu sei que dimensionar reservatórios de concreto armado pode ser uma tarefa bem complexa. Mas fique tranquilo, nesse post eu vou explicar da maneira mais simplificada possível como você irá dimensionar seus reservatórios.
Introdução
Um reservatório é composto com um conjunto de paredes cujo objetivo é o armazenamento de água.
Apesar de que podermos dimensionar paredes com 12 cm de espessura, devido aos cobrimentos mínimos presentes na ABNT/NBR: 6118 (2014), é recomendado uma espessura mínima de 15 cm para as paredes.
Essas paredes estão apoiadas em pilares, normalmente os pilares que circundam a caixa de elevador.
Carregamentos atuantes nos reservatórios
As cargas atuantes nas paredes dos reservatórios são tanto perpendiculares ao plano médio da parede, ocasionando o funcionamento como placas (como exemplo de placas temos as lajes), e também atuam no próprio plano médio da parede, trabalhando assim como vigas ou vigas-parede.
Laje de tampa
Na laje de tampa atuam o peso próprio, o revestimento e o carregamento acidental.
O peso próprio é calculado conforme fazemos em lajes maciças, apenas multiplicando a espessura em metros pelo peso específico do concreto armado, que vale \mathrm{25 \; kN/m^3}.
Em situações usuais utiliza-se como revestimento \mathrm{1,0 \; kN/m^2} e como carregamento acidental \mathrm{0,5 \; kN/m^2}.
Laje de fundo
Os carregamentos atuantes na laje de fundo serão bem similares aos atuantes na laje de tampa. Como diferença, removeremos o carregamento acidental e incluiremos o carregamento decorrente da água acima da laje, apenas multiplicando a altura de água por \mathrm{10 \; kN/m^3}, resultando em um carregamento por unidade de área \mathrm{kN/m^2}.
Paredes
Na parede consideraremos o uma carga horizontal e triangular decorrente do empuxo da água. Essa carga parte de zero no topo dos reservatórios e vai até seu valor máximo, \mathrm{10 \cdot h \; kN/m^2}, no fundo dos reservatórios.
Calculando os reservatórios como lajes
Para realizarmos cálculos manuais é comum isolarmos cada elemento e analisarmos separadamente. Da mesma forma como fazemos com lajes maciças, podemos utilizar tabelas simplificadas para obtermos os esforços nas paredes.
Condições de contorno
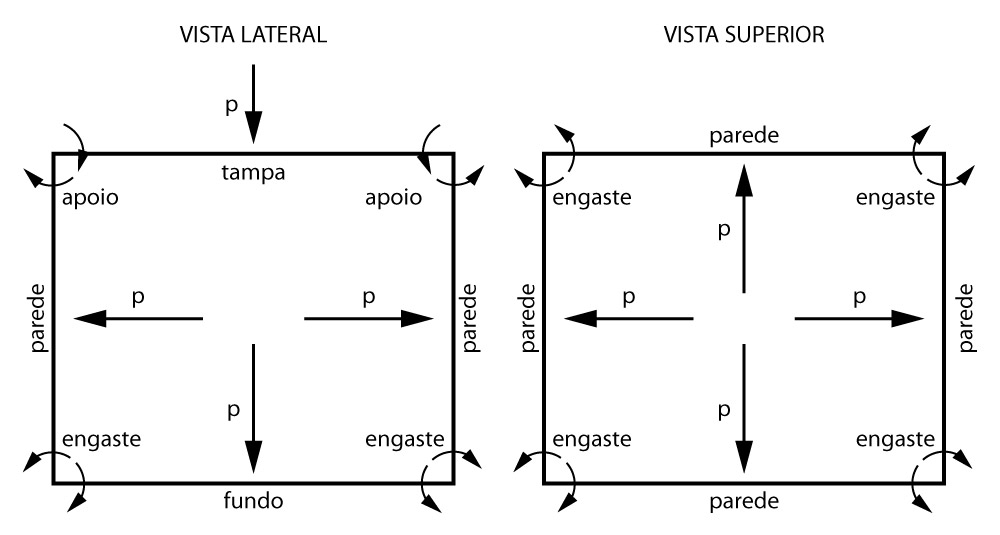
Analisando as condições de contorno vamos seguir a seguinte premissa: quando duas lajes tende à girar no mesmo sentido consideraremos aquele encontro como um apoio simples. Em caso contrário, ou seja, se tendem a girar em sentido oposto, consideraremos aquela extremidade como um engaste, uma vez que, ali existirá uma restrição à rotação.
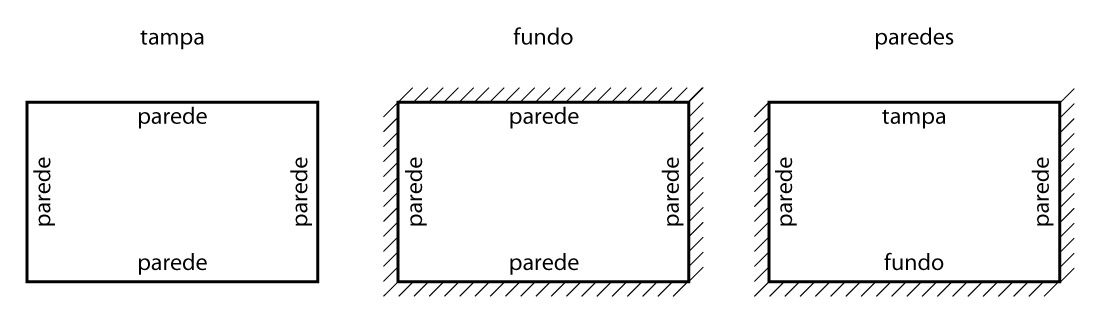
Nas vistas apresentadas acima, podemos concluir que:
- cada parede é engastada nas paredes de extremidade e na laje de fundo e é simplesmente apoiada na tampa;
- a laje de fundo é considerada engastada em todas as paredes;
- a tampa é simplesmente apoiada nas paredes laterais.
As condições de contorno recém apresentadas são resumidas na imagem abaixo:
Tabelas de Czerny
Para facilitar a sua vida vou repetir as tabelas de Czerny também nessa publicação:
Nos casos mais gerais, utilizaremos apenas a primeira tabela para tampa, a antepenúltima para o fundo e as duas últimas para as paredes.
Compatibilização dos momentos fletores
Lembrando do processo que fizemos com lajes maciças, ainda temos que compatibilizar os momentos negativos entre as lajes. Para isso, observe a situação apresentada na figura abaixo:
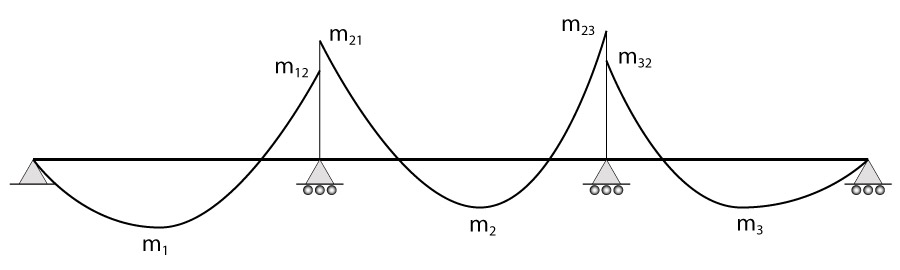
Como os esforços nas lajes foram obtidos separadamente, observe que os momentos negativos nos encontros são diferentes. Os momentos \mathrm {m_{12}} e \mathrm {m_{21}} resultam em um momento compatibilizado a partir da formulação abaixo:
\mathrm{ {m_{12}}^* \geq \left\{ \begin{array}{ll} \dfrac{m_{12} + m_{21}}{2} \\ 0,8 \cdot m_{21} \end{array} \right. }
Nesse caso, \mathrm {m_{12}} e \mathrm {m_{21}} representam os momentos negativos entre das lajes, sendo o último o maior dos dois.
De modo similar podemos, obtemos o momento negativo compatibilizado no encontro entre a laje 2 e a laje 3:
\mathrm{ {m_{23}}^* \geq \left\{ \begin{array}{ll} \dfrac{m_{23} + m_{32}}{2} \\ 0,8 \cdot m_{23} \end{array} \right. }
Observe que chegamos a momentos negativos inferiores a \mathrm {m_{21}} e \mathrm {m_{23}}. Dessa forma, como o diagrama da laje 2 foi deslocado para baixo também devemos aumentar o valor do momento fletor positivo nessa laje. Podemos seguir a seguinte formulação:
\mathrm{{m_2}^* = m_2 + \dfrac{m_{21} - {m_{12}}^*}{2} + \dfrac{m_{23} - {m_{23}}^*}{2}}
Dimensionamento como viga ou viga-parede
No caso das paredes, além do dimensionamento como laje, também é necessário o dimensionamento como viga ou viga-parede, uma vez que o carregamento também atua paralelamente ao plano médio do elemento.
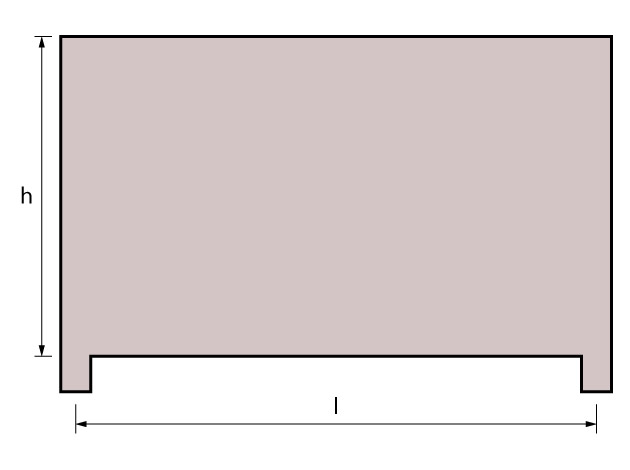
Inicialmente vamos verificar se a mesma deve ser considerada uma viga-parede ou viga esbelta. Considerando \mathrm {l} o vão de cálculo e \mathrm {h} a altura da viga, uma viga biapoiada pode ser considerada viga-parede quando:
\mathrm{\dfrac{l}{h} < 2,0}
As formulações apresentadas nessa publicação são para o caso de vigas-parede que seguem a seguinte proporção:
\mathrm{1,0 < \dfrac{l}{h} <2,0}
Dessa forma, no caso das dimensões indicarem que a parede se trata de uma viga usual, não repetiremos aqui pois já foi tratado em publicações anteriores.
Armadura do banzo tracionado
O cálculo da área de aço para vigas-parede utiliza a mesma formulação para vigas esbeltas:
\mathrm{A_s = \dfrac{M_d}{Z \cdot f_{yd}}}
A primeira grande diferença nas duas considerações é a forma como obteremos o braço de alavanca (\mathrm{Z}. Para vigas-parede biapoiadas podemos adotar o seguinte valor como braço de alavanca:
\mathrm{Z = 0,15 \cdot h \cdot \left( 3 + \dfrac{l}{h} \right)}
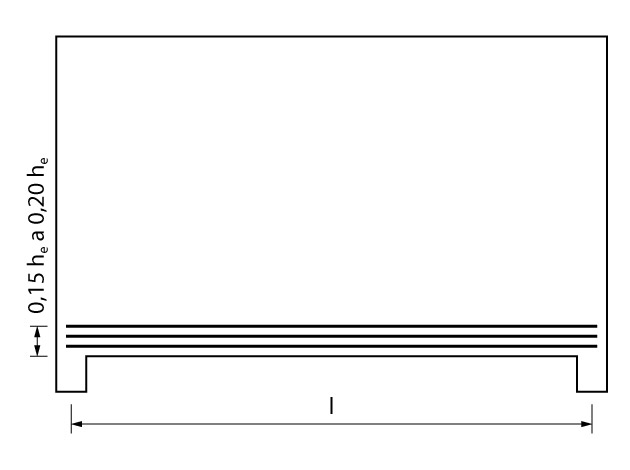
A área de aço encontrada para o banzo deve ser distribuída em uma faixa de \mathrm{0,15 \cdot h_e} e \mathrm{0,20 \cdot h_e}. Onde \mathrm{h_e} é o menor valor entre \mathrm{h} e \mathrm{l}.
Armadura mínima para vigas-parede
Araújo (2014) propõe uma relação entre a armadura mínima de vigas-parede e a armadura mínima de vigas esbeltas:
\mathrm{A_{s,minVP} = \lambda \cdot A_{s,minVE}}
Onde o \mathrm{\lambda} pode obtido na tabela abaixo:
| \mathrm{\dfrac{l}{h}} | \mathrm{\lambda} |
|---|---|
| 2,0 | 1,00 |
| 1,5 | 0,90 |
| 1,25 | 0,75 |
| 1,0 | 0,55 |
Tensões de compressão apoio das paredes dos reservatórios
Ao verificarmos vigas-parede é necessário também a verificação do esmagamento do concreto da região dos apoios. Para isso verificaremos a tensão na biela inclinada (\mathrm{\sigma_{2d}}) e a tensão na direção vertical no apoio em si (\mathrm{\sigma_d})
Podemos calcular \mathrm{\sigma_d} pela equação abaixo:
\mathrm{\sigma_d = \dfrac{R_d}{b \cdot c}}
Onde:
- \mathrm{R_d} vale o valor de cálculo da reação de apoio;
- \mathrm{b} equivale á largura da viga;
- \mathrm{c} vale o comprimento do apoio.
A tensão na biela inclinada vale:
\mathrm{\sigma_d = \dfrac{R_d}{b \cdot (c + cotg \theta) \cdot sen^2 \theta}}
Onde \mathrm{\theta} vale a inclinação da biela e pode ser calculado por:
\mathrm{\theta = arctg \left( \dfrac{4 \cdot Z}{l} \right) }
Os valores de tensão acima apresentados devem ser inferiores a \mathrm{f_{cdr} = 0,60 \cdot \left( 1 - \dfrac {f_{fck}}{250} \right) \cdot f_{cd}}.
De maneira geral, podemos fazer a seguinte consideração:
- caso \mathrm{u = 2 \cdot d' \geq c \cdot cotg \theta \rightarrow \sigma_d \leq f_{cdr}}
- caso \mathrm{u = 2 \cdot d' < c \cdot cotg \theta \rightarrow \sigma_{2d} \leq f_{cdr}}
Ancoragem da armadura de flexão para paredes de reservatórios
Por fim, vamos verificar agora a ancoragem da armadura de flexão das paredes.
É possível considerar uma redução do comprimento de ancoragem no caso de utilização de ganchos, que em reservatórios é recomendado utilizar-los no plano horizontal. Desse modo, o comprimento de ancoragem será \mathrm{0,7 \cdot l_b}.
Na região do apoio é necessário ancorar um área de aço de 80 % da área calculada para o banzo tracionado.
Assim sendo, ainda é possível reduzir o comprimento de ancoragem pela razão entre área de aço necessária por área de aço efetiva:
\mathrm{l_{b,nec} = 0,7 \cdot l_b \cdot \dfrac{0,8 \cdot A_s}{A_{s,ef}}}
Recado final
Espero que essa publicação tenha tratado todas as suas dúvidas referentes à dimensionamento de reservatórios elevados. Além do dimensionamento da área de aço ainda trataremos sobre detalhamento, verificações de fissuração além de exemplos práticos em posts futuros.
Caso ainda tenha sobrado alguma dúvida, não hesite em escrever nos comentários abaixo.
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 4
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

São excelentes as aulas.
Muito obrigado, Joaquim!
FIQUEI GRATAMENTE IMPRESSIONADO PELA ABORDAGEM SIMPLES.OBRIGADO
Valeu, Carlos!