Você saberia o que fazer caso o sua verificação com o parâmetro de instabilidade alfa retornasse em uma estrutura de nós móveis? Pois é, um dos problemas do parâmetro alfa é que o mesmo não fornece o valor do efeito de segunda ordem em si.
Dessa forma, uma outra solução é utilizarmos o coeficiente Gama-z, também presente na ABNT/NBR: 6118 (2014), tanto para classificarmos a estrutura em nós fixos e nós móveis, quanto para majorarmos os esforços a fim de considerar os esforços de segunda ordem.
Introdução ao Coeficiente Gama-Z
O coeficiente gama-z, dado para cada combinação de carregamento, é obtido a partir da equação abaixo:
\mathrm{\gamma_z = \dfrac{1}{1 - \dfrac{\Delta M_{tot,d}}{M_{1,tot,d}}}}
Em que \mathrm{M_{1,tot,d}} é dado pelos momentos de primeira ordem, ou seja, soma dos momentos de todas as forças horizontais em relação à base da estrutura e \mathrm{\Delta M_{tot,d}} equivale ao somatório dos produtos das forças verticais pelos respectivos deslocamentos horizontais.
Ao subtrairmos o resultado obtido por 1,0, teremos o percentual dos esforços de segunda ordem.
Vamos lembrar que, a norma brasileira considera como estruturas de nós fixos aquela em que os esforços de segunda ordem são inferiores a 10% dos esforços de primeira ordem. Assim sendo, são estruturas de nós fixos aquelas em que o coeficiente é inferior a 1,1.
Caso você prefira, também pode acompanhar esse conteúdo a partir do vídeo abaixo:
Consideração dos esforços de segunda ordem
A norma brasileira nos fornece uma metodologia para considerarmos, de maneira aproximada, os esforços globais de segunda ordem. Para isso, basta que majoremos os esforços horizontais por \mathrm{0,95 \cdot \gamma_z}. Esse processo só é válido para edifícios em que \mathrm{\gamma_z \leq 1,3}.
Apenas como exemplo, imagine um edifício em que calculamos um gama-z de 1,2. Como o valor encontrado é superior a 1,1, a estrutura é considerada como nós móveis e devemos considerar os efeitos de segunda ordem. Assim, vamos majorar as ações horizontais pelo fator abaixo:
\mathrm{0,95 \cdot \gamma_z = 0,95 \cdot 1,2 = 1,14}
Consideração da não-linearidade física
A fim de calcular os esforços e os deslocamentos considerando, de modo simplificado, a não-linearidade física, podemos reduzir a rigidez das lajes, vigas e dos pilares.
No caso de lajes, teremos:
\mathrm{\left( E \cdot I \right)_{sec} = 0,3 \cdot E_c \cdot I_c}
Para as vigas, a redução irá variar de acordo com a relação de armação comprimida e tracionada:
\mathrm{\left( E \cdot I \right)_{sec} = 0,4 \cdot E_c \cdot I_c} para \mathrm{A_s' \neq A_s}
\mathrm{\left( E \cdot I \right)_{sec} = 0,5 \cdot E_c \cdot I_c} para \mathrm{A_s' = A_s}
Por fim, para pilares segue a redução abaixo:
\mathrm{\left( E \cdot I \right)_{sec} = 0,8 \cdot E_c \cdot I_c}
O valor de \mathrm{E_c}, analogamente ao feito para o parâmetro alfa, será o módulo de deformação secante do concreto majorado em 10%.
Exemplo sobre Coeficiente Gama-Z
Com o intuito de aplicarmos o estudado nessa publicação, vamos prosseguir com nosso edifício exemplo e assim, calcularmos o coeficiente gama-z para o mesmo.

Para esse edifício, nós já obtivemos a ação de vento repartida para cada pórtico, assim como a ação de decorrente da imperfeição geométrica global. Ainda na publicação de imperfeição geométrica, obtivemos que deveremos considerar a ação conjunta do vento e do desaprumo.
Combinações de carregamento
Para esse exemplo, vamos considerar o caso em que o vento é a ação variável principal. Dessa forma, teremos:
\mathrm{1,4 \cdot g + 1,4 \cdot 0,5 \cdot q + 1,4 \cdot \left( v + d \right)}
Em que \mathrm{g} equivale aos carregamentos permanentes, \mathrm{q} representa a sobrecarga de utilização, \mathrm{v} indica a ação do vento e \mathrm{d} equivale ao desaprumo.
A fim de simplificarmos a resolução, vamos considerar que \mathrm{q \approx 0,15 \cdot g}. Assim sendo, e sabendo que \mathrm{p = g + q}, teremos a seguinte combinação:
\mathrm{1,3 \cdot p + 1,4 \cdot \left( v + d \right)}
Onde \mathrm{p} vale o somatório das forças verticais.
Esforços de primeira ordem
Com o intuito de obter os esforços de primeira ordem, podemos simplesmente utilizar os momentos já calculados do vento e da imperfeição geométrica e multiplica-los por 1,4.
\mathrm{M_{1,tot,d} = 1,4 \cdot \left( 1.818 + 789 \right)}
\mathrm{M_{1,tot,d} = 3.650 \; kN \cdot m}
Observação: as valores dos momentos utilizados acima foram obtidos na publicação de imperfeição geométrica global.
Esforços de segunda ordem
Em primeiro lugar, vamos obter o módulo de deformação a ser utilizado em nosso modelo numérico.
Módulo de deformação
Para isso, vamos começar com o módulo de elasticidade inicial:
\mathrm{E_{ci} = \alpha_E \cdot 5.600 \cdot \sqrt{f_{ck}}}
\mathrm{E_{ci} = 1,0 \cdot 5.600 \cdot \sqrt{30} = 30.672 \; MPa}
E, posteriormente, o módulo de elasticidade secante:
\mathrm{E_{cs} = \left( 0,8 + 0,2 \cdot \dfrac{f_{ck}}{80} \right) \cdot E_{ci}}
\mathrm{\left( 0,8 + 0,2 \cdot \dfrac{30}{80} \right) \cdot E_{ci} = 26.838 \; MPa}
Podemos agora aplicar a majoração de 10% no módulo de deformação secante:
\mathrm{E_c = 1,1 \cdot E_{cs} = 29.522 \; MPa}
A fim de considerar a não-linearidade física, vamos utilizar em nosso modelo no Ftool \mathrm{0,4 \cdot E_c} para as vigas e \mathrm{0,8 \cdot E_c} para os pilares.
Deslocamentos horizontais
Em segundo lugar, vamos calcular os deslocamentos ocasionados pelas forças horizontais de cálculo: \mathrm{1,4 \cdot \left( v + d \right)}.
Como exemplo, analisaremos assim o pórtico central. As ações do vento e do desaprumo aplicadas à esse pórtico já foram calculadas anteriormente. A tabela abaixo apresenta os valores em cada basicamente o valor combinado.
| z (m) | Vento (kN) | Desaprumo (kN) | 1,4 (V + D) (kN) |
|---|---|---|---|
| 3,0 | 4,27 | 2,35 | 9,3 |
| 6,0 | 5,19 | 2,35 | 10,6 |
| 9,0 | 5,64 | 2,35 | 11,2 |
| 12,0 | 6,10 | 2,35 | 11,8 |
| 15,0 | 6,41 | 2,35 | 12,3 |
| 18,0 | 3,36 | 1,95 | 7,4 |
Em seguida, aplicando a ação combinada para cada pavimento e alterando o módulo de deformação do concreto para vigas e pilares, encontraremos os deslocamentos horizontais em cada pavimento:
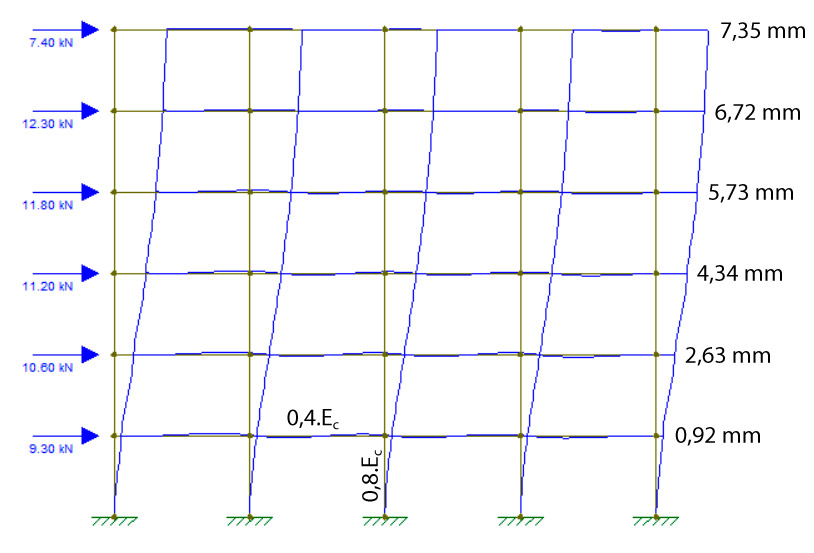
Nós utilizaremos o valor médio de deslocamento:
\mathrm{\delta = \dfrac{0,92+ \cdots +7,35}{6} = 4,62 \; mm}
Resultado dos esforços de segunda ordem
Como somatório das forças verticais, podemos utilizar o valor encontrado na verificação do parâmetro de instabilidade alfa. O mesmo foi obtido considerando 12 kN/m² para laje de piso e 10 kN/m² para laje de cobertura, totalizando assim 42.000 kN.
Dessa forma, multiplicando o somatório das forças verticais pelo deslocamento médio, teremos os esforços de segunda ordem:
\mathrm{\Delta M_{tot,d} = 1,3 \cdot 42.000 \cdot 0,462}
\mathrm{\Delta M_{tot,d} = 25.225 \; kN \cdot cm}
Cálculo do Coeficiente Gama-Z
Por fim, vamos utilizar a formulação do gama-z:
\mathrm{\gamma_z = \dfrac{1}{1 - \dfrac{\Delta M_{tot,d}}{M_{1,tot,d}}}}
\mathrm{\gamma_z = \dfrac{1}{1 - \dfrac{25.225}{365.000}} = 1,07}
Assim sendo, o esforços de segunda ordem equivalem a 7% dos esforços de primeira ordem. Dessa forma, podemos classificar a estrutura como nós fixos, desconsiderando assim os esforços de segunda ordem.
Recado final
Ao final dessa publicação, eu espero que você seja capaz de obter o Coeficiente Gama-Z de um edifício e assim analisar a magnitude dos esforços globais de segunda ordem.
Não esqueça de compartilhar esse conteúdo com aquele seu amigo que também tem interesse em estruturas.
Um forte abraço e até a próxima!
Otimize seus cálculos de engenharia em minutos. Experimente o Calculadoras de Engenharia.

muito, bom gostei
Valeu, Ronio!