Visto que já conhecemos o valor da ação do vento em edificações de concreto armado, vamos estudar outra ação horizontal que deve ser avaliada em toda edificação: a imperfeição geométrica global, também conhecida como desaprumo, uma vez que, não podemos evitar esse tipo de imprecisão em nossas estruturas.
Cálculo da imperfeição geométrica
Conforme presente na norma brasileira ABNT/NBR: 6118 (2014), a imperfeição geométrica deve ser considerada através de uma inclinação de desaprumo, assim como ilustra a figura a seguir:
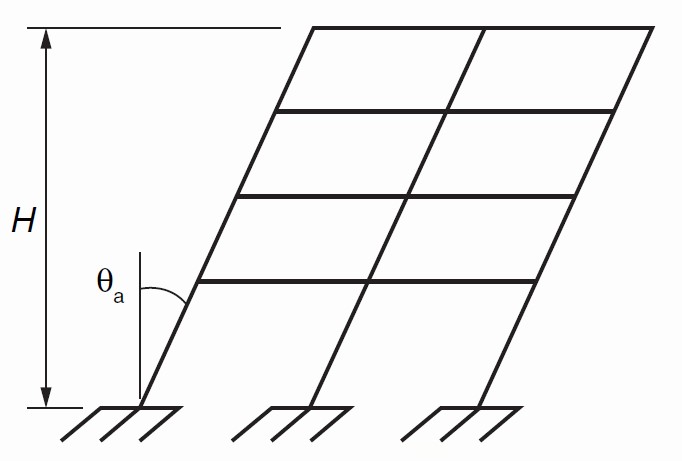
O valor de \mathrm{\theta_a} é fornecido pela equação abaixo:
\mathrm{\theta_a = \theta_1 \cdot \sqrt{\dfrac{1 + 1/n}{2}}}
Onde \mathrm{n} vale o número de pilares no pórtico e \mathrm{\theta_1} é dado pela formulação abaixo:
\mathrm{\theta_1 = \dfrac{1}{100 \cdot \sqrt{H}}}
Em que \mathrm{H}, bem como ilustra a figura, equivale a altura total da edificação em metros.
Ainda segundo a norma supracitada, o valor máximo para o \mathrm{\theta_1} é 1/200 e, no caso de estruturas reticuladas e imperfeições locais, o valor mínimo é 1/300.
Além disso, para edifícios com predominância de lajes lisas ou cogumelo, teremos \mathrm{\theta_a=\theta_1} e, para pilares isolados em balanços, \mathrm{\theta_1= 1/200}.
Encontrando uma força equivalente
Uma vez que já conhecemos o valor do desaprumo. Vamos obter agora a força equivalente para representar o seu efeito.
Em primeiro lugar, vamos imaginar um pilar submetido a um desaprumo \mathrm{\theta} e um carregamento \mathrm{F_v}, que representa as cargas verticais atuantes em um pavimento.
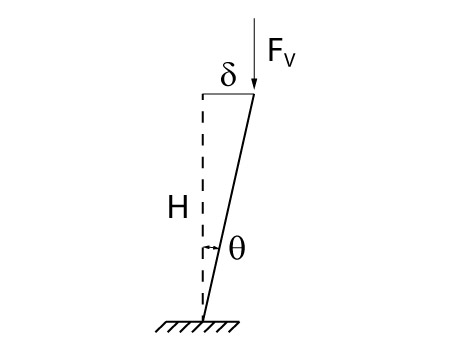
Em segundo lugar, vamos obter, através da relação \mathrm{H} e \mathrm{\theta} o deslocamento no pavimento analisado:
\mathrm{\delta = H \cdot \theta}
Logo após, vamos calcular o momento na base ocasionado pela força vertical e assim, calcular uma força horizontal que cause esse mesmo momento na base.
\mathrm{M_V = F_V \cdot \delta}
\mathrm{M_H = F_H \cdot H = F_V \cdot H \cdot \theta}
Por fim, simplificando a equação acima, chegaremos em uma força horizontal equivalente para a imperfeição geométrica global nesse pavimento:
\mathrm{F_H = F_V \cdot \theta}
Assim sendo, podemos calcular uma força horizontal de desaprumo para cada pavimento apenas multiplicando a força vertical naquele pavimento pelo valor da imperfeição geométrica.
Em síntese, calculamos uma força horizontal que gere o mesmo momento ocasionado pelo deslocamento da força vertical.
Considerações das imperfeições geométricas
Ainda de acordo com a norma brasileira, a consideração ou não da ação do desaprumo é analisada de acordo com as seguintes possibilidades:
b) Quando a ação do vento for inferior a 30 % da ação do desaprumo, considera-se somente o desaprumo respeitando a consideração de \mathrm{\theta_{1min}}, conforme definido acima.
c) Nos demais casos, combina-se a ação do vento e desaprumo, sem necessidade da consideração do \mathrm{\theta_{1min}}. Nessa combinação, admite-se considerar ambas as ações atuando na mesma direção e sentido como equivalentes a uma ação do vento, portanto como carga variável, artificialmente amplificada para cobrir a superposição.ABNT NBR: 6118 (2014)
A fim de simplificar as colocações acima, preparei o fluxograma abaixo:
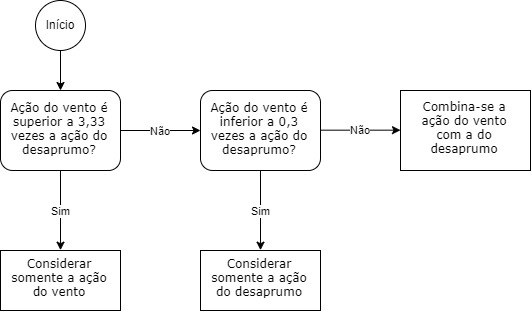
Para a comparação entre vento e desaprumo, a norma recomenda utilizarmos os momentos totais da base da construção para cada direção. No caso do desaprumo, não é necessário considerar o \mathrm{\theta_{1min}}.
Mais um detalhe a se observar é que o desaprumo não precisa ser considerado no Estado Limite de Serviço.
Exemplo de cálculo de imperfeição geométrica
A fim de aplicarmos o conteúdo estudado até o momento, vamos calcular as forças de desaprumo em um edifício que já calculamos a ação do vento e analisarmos se precisaremos ou não considerar as forças de desaprumo.
O edifício em questão tem 20,0 m por 30,0 m de dimensões de base e 6 pés-direitos de 3,0 m, totalizando uma altura de 18,0 m.

Caso você prefira, também pode acompanhar a resolução a partir do vídeo abaixo:
Ação do vento
Primeiramente, vamos calcular o momento total na base da edificação proporcionado pelo vento, a fim de, em seguida, compararmos com os esforços de desaprumo.
Com o intuito de calcular o momento acima citado, vamos utilizar uma tabela, apresentada na publicação anterior, que contém as forças de arrasto aplicadas em cada pavimento.
A fim de encontrarmos o momento na base causado por cada força, basta que multipliquemos a força aplicada em cada pavimento pela ordenada da mesma, vide tabela:
| z (m) | \mathrm{F_a \; (kN)} | M (kN.m) |
|---|---|---|
| 3,0 | 23,9 | 71,7 |
| 6,0 | 29,1 | 174,6 |
| 9,0 | 31,6 | 284,4 |
| 12,0 | 34,2 | 410,4 |
| 15,0 | 35,9 | 538,5 |
| 18,0 | 18,8 | 338,4 |
Assim sendo, o somatório do momentos na base da edificação causados pela ação do vento vale:
\mathrm{M_v = 71,7+174,6+284,4+ \cdots}
\mathrm{\cdots +410,4+538,5+338,4}
\mathrm{M_v = 1.818 \; kN \cdot m}
Imperfeição geométrica global
Com o propósito de calcularmos os momentos da base devido aos esforços ocasionados pela imperfeição geométrica global, vamos primeiramente obter o somatório das forças verticais em cada pavimento.
Para isso, conforme fizemos na análise da estabilidade global, vamos considerar de maneira aproximada, como somatório das cargas verticais, o valor de \mathrm{12 \; kN/cm^2} para lajes de piso e \mathrm{10 \; kN/cm^2} para lajes de forro.
Assim sendo, uma vez que a área do pavimento é de 600 m² (20 m x 30 m), teremos as seguintes cargas verticais:
\mathrm{F_{piso} = 600 \cdot 12 = 7.200 \; kN}
\mathrm{F_{forro} = 600 \cdot 10 = 6.000 \; kN}
Consideração ou não do desaprumo
Em seguida, vamos calcular o valor do desaprumo em si. Vamos começar pelo cálculo do \mathrm{\theta_1}:
\mathrm{\theta_1 = \dfrac{1}{100 \cdot \sqrt{H}}}
\mathrm{\theta_1 = \dfrac{1}{100 \cdot \sqrt{18}} = \dfrac{1}{424}}
Visto que estamos apenas verificando a necessidade de consideração da imperfeição geométrica global, não é necessário levar o \mathrm{\theta_{1min}} em consideração.
Logo depois, vamos calcular o valor do desaprumo, lembrando que para direção verificada temos pórticos com 5 prumadas de pilares:
\mathrm{\theta_a = \theta_1 \cdot \sqrt{\dfrac{1 + 1/n}{2}}}
\mathrm{\theta_a = \dfrac{1}{424} \cdot \sqrt{\dfrac{1 + 1/5}{2}} = \dfrac{1}{548} }
Sendo assim, podemos calcular a força horizontal de desaprumo para os pavimentos tipo e cobertura:
\mathrm{F_{H,piso} = 7.200 \cdot \dfrac{1}{548} = 13,15 \; kN}
\mathrm{F_{H,cobertura} = 6.000 \cdot \dfrac{1}{548} = 10,95 \; kN}
Analogamente ao que fizemos com a ação do vento, vamos calcular o somatório dos momentos causados pelas imperfeições geométricas na base da estrutura:
| z (m) | \mathrm{F_d \; (kN)} | M (kN.m) |
|---|---|---|
| 3,0 | 13,15 | 39,45 |
| 6,0 | 13,15 | 78,90 |
| 9,0 | 13,15 | 118,35 |
| 12,0 | 13,15 | 157,80 |
| 15,0 | 13,15 | 197,25 |
| 18,0 | 10,95 | 197,10 |
Portanto, o somatório de momentos da base da edificação vale 788,85 kN.m.
Por fim, podemos utilizar o fluxograma já apresentado anteriormente para analisar a consideração dos esforços de desaprumo:
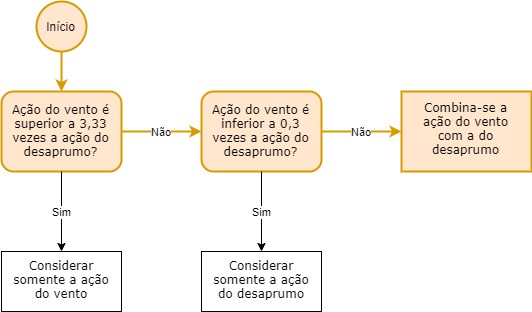
Conforme posto no fluxograma, devemos combinar a ação do vento, juntamente com a ação do desaprumo, em uma mesma direção como uma única ação variável.
Repartição da imperfeição geométrica global entre os pórticos
A fim de repartimos a ação de desaprumo entre os pórticos, podemos utilizar o mesmo processo que fizemos para a ação do vento. Assim sendo, para esse edifício teremos que 14,3% da força de desaprumo (1,88 kN) será aplicada em cada pórtico de extremidade e 17,85% da força de desaprumo (2,35 kN) será aplicada em cada pórtico intermediário.
Recado final
Em suma, o objetivo dessa publicação foi lhe passar os conhecimentos necessários para calcular o esforços oriundos da imperfeição geométrica global e analisar a possibilidade de dispensar a mesma.
Caso tenha ficado com alguma dúvida não esqueça de deixar nos comentários abaixo.
Um forte abraço e até a próxima!
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
