Eu acredito que você já tenha visto no seu estágio, ou mesmo em uma visita a uma obra, lajes nervuradas que apresentam suas nervuras em duas direções.
É comum visualizar diretamente as nervuras em garagens, uma vez que neste local não são usualmente utilizados forros.

Antes de prosseguir nesse post, recomendo bastante que estude sobre o dimensionamento de lajes nervuradas em uma direção.
Introdução
Assim como nas lajes nervuradas em uma direção (as lajes com treliça ou vigotas), nas lajes nervuradas em duas direções também são utilizados enchimentos para que as nervuras sejam formadas. Sendo que, para duas direções, são utilizadas usualmente EPS e cubas plásticas como enchimento.
Essas lajes apresentam economia de concreto quando comparadas com as lajes maciças mas quando comparadas com as lajes nervuradas em uma direção elas apresentam menores deslocamentos, uma vez que trabalham nas duas direções.
Modelo de cálculo
A obtenção de esforços para lajes com nervuras em duas direções é obtida de maneira mais coerente com a utilização de um modelo de grelha. Entretanto, para tornar essa publicação mais aplicável, obteremos o esforço pela utilização da tabela de Czerny.
Método simplificado
Para obtenção dos esforços por métodos simplificados, utilizaremos as tabelas de Czerny, conforme realizado para lajes maciças.
Como dado de entrada para a tabela de Czerny utilizaremos as condições de contorno (livre, apoiada, engastada) e também a relação entre as dimensões nas duas direções da laje, \mathrm{\lambda} .
\mathrm{\lambda = \dfrac{l_y}{l_x}}
Você pode conferir nas tabelas abaixo os valores de \mathrm{m_x} e \mathrm{m_y} para cada situação.
Com os valores retirados é possível obter o momento por metro para as duas direções a partir da formulação abaixo:
\mathrm{M_x = \dfrac{p \cdot l_x^2}{m_x}}
\mathrm{M_y = \dfrac{p \cdot l_x^2}{m_y}}
Como até então obtivemos os esforços conforme as lajes maciças e os mesmos são, normalmente, inferiores aos apresentados por lajes nervuradas, será necessário realizar uma correção nos valores.
Hahn (1972) apresenta o coeficiente que deve multiplicar o esforço encontrado através de tabelas simplificadas a fim de corrigir essa imprecisão:
\mathrm{\delta = \dfrac{1}{1 - \left( \dfrac{5}{6} \cdot \dfrac{ \epsilon^2}{1 + \epsilon^4} \right)} }
Então, o procedimento é basicamente calcular os esforços como uma laje maciça e multiplicar cada esforço por \mathrm{\delta}.
Exemplo aplicado
Para facilitar o entendimento desse assunto, a partir de agora seguiremos com o exemplo aplicado para que você aprenda como dimensionar a armadura de flexão de uma laje com nervuras em duas direções.
Vamos considerar uma laje em que a distância entre eixos das vigas de apoio é de 6,0 m em uma direção e 5,0 m na outra, vide figura abaixo.
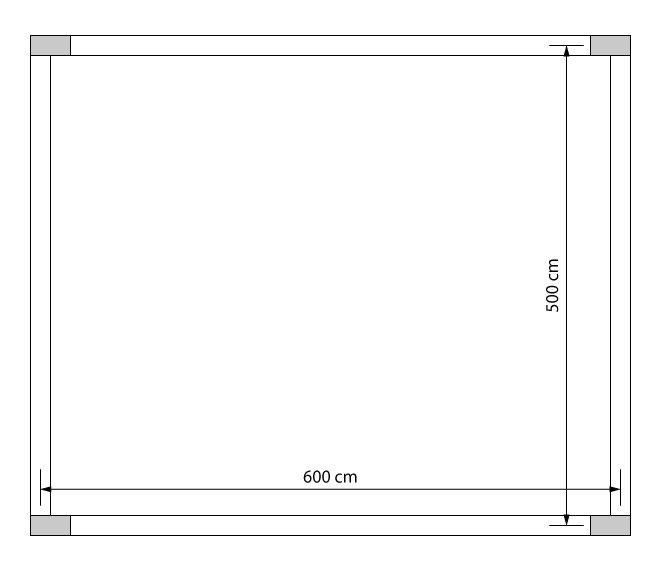
Nessa laje será utilizado EPS, com as dimensões de base 50 cm x 50 cm e 12 cm de altura, como enchimento. A largura da nervura será de 12 cm e a espessura da capa de 4 cm.
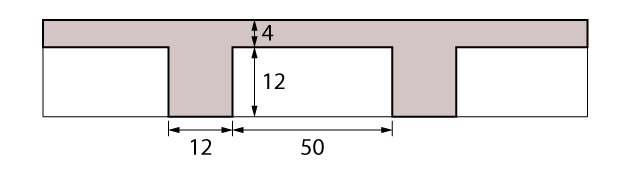
Ainda quanto aos dados de entrada, para o concreto será considerado classe C25 (resistência característica de 25 MPa) e aço CA50 (tensão de escoamento de 500 MPa).
Levantamento das ações
A primeira etapa para o dimensionamento da laje é o levantamento das ações.
Diferentemente das lajes unidirecionais, agora vamos obter os valores distribuídos por unidade de área, uma vez que pretendemos utilizar a tabela de Czerny.
Sobrecarga de utilização e revestimento
A sobrecarga de utilização (também denominado de carga acidental) e o revestimento já valores que estão distribuídos por área.
Os valores de ambos podem ser obtidos a partir da ABNT/NBR: 6120 (2019) e para o exemplo serão considerados, respectivamente, \mathrm{1,5 \; kN/m^2} (considerando um quarto, por exemplo) e \mathrm{1,0 \; kN/m^2}.
Capa de concreto
Para a capa também podemos chegar facilmente a um valor distribuído por unidade de área apenas multiplicando a espessura da mesma pelo peso específico do concreto:
\mathrm{0,04 \cdot 25 = 1,0 \; kN/m^2}
Concreto das nervuras e enchimentos
Vamos calcular agora o peso de concreto na região das nervuras e do enchimento para a área destacada abaixo:
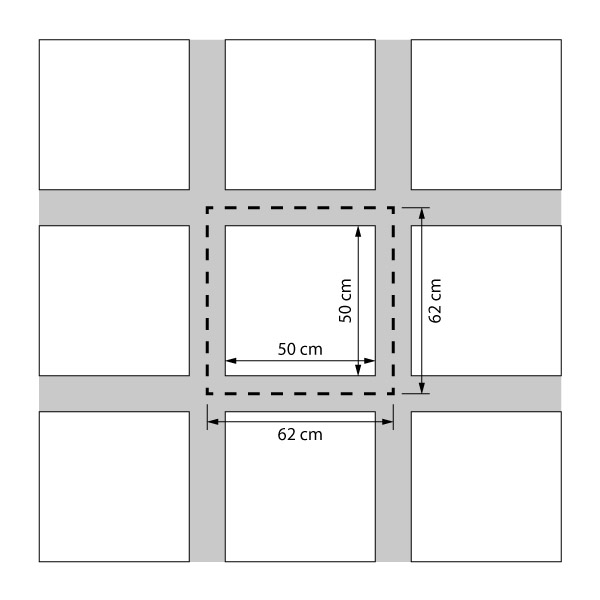
Estamos destacando essa região porque o mesmo valor irá se repetir a cada área de \mathrm{0,62 \cdot 0,62}.
Dentro da área tracejada, nós temos nas nervuras o seguinte volume:
\mathrm{4 \cdot 0,5 \cdot 0,06 \cdot 0,12 + \cdots}
\mathrm{\cdots + 4 \cdots 0,06 \cdot 0,06 \cdot 0,12 = 0,016128 \; m^3}
Com esse volume de concreto das nervuras, podemos calcular o peso apenas multiplicando pelo peso específico do concreto:
\mathrm{0,016128 \cdot 25 = 0,4032 \; kN}
Para calcular o peso do enchimento, vamos considerar o peso específico de 20 kg/m³. Dessa forma, o peso localizado na área tracejada pode ser calculado multiplicando o volume do EPS por seu peso específico:
\mathrm{0,5 \cdot 0,5 \cdot 0,12 \cdot 0,20 = 0,006 \; kN}
Lembrando que o peso de concreto referente as nervuras e o peso do enchimento ocorre a cada área de 0,3844 m² (0,62 x 0,62), podemos obter cada um desses pesos por unidade de comprimento:
\mathrm{\dfrac{ 0,4032 }{0,3844} = 1,05 \; kN/m^2}
\mathrm{\dfrac{0,006}{0,3844} = 0,016 \; kN/m^2}
Carregamento total
Com isso, temos todos os carregamentos atuantes na laje distribuídos por unidade de área:
\mathrm{p = 1,5+1,0+1,0+1,05+0,016= 4,6 \; kN/m^2 }
Obtenção dos esforços
Antes de entrarmos na tabela é necessário calcular o valor de \mathrm{\lambda} que relaciona as dimensões nas duas direções:
\mathrm{\lambda = \dfrac{l_y}{l_x} = \dfrac{600}{500} = 1,2}

Entrando na tabela para a situação de quatro bordas apoiadas e \mathrm{\lambda = 1,2} obtemos 16,9 e 22,3, respectivamente para mx e my.
Sendo assim, podemos agora calcular o momento fletor para cada metro de largura para as duas direções:
\mathrm{M_x = \dfrac{ p \cdot l_x ^2 }{m_x} }
\mathrm{M_x = \dfrac{ 4,6 \cdot 5,0 ^2 }{16,9} = 6,8 \; kN \cdot m/m }
\mathrm{M_y = \dfrac{ p \cdot l_x ^2 }{m_y} }
\mathrm{M_y = \dfrac{ 4,6 \cdot 5,0 ^2 }{22,3} = 5,16 \; kN \cdot m/m }
Correção dos esforços
Agora que já temos os esforços calculados supondo uma laje maciça, vamos corrigir o esforços multiplicando pelo coeficiente citado por Hahn (1972).
\mathrm{\delta = \dfrac{1}{1 - \left( \dfrac{5}{6} \cdot \dfrac{ \epsilon^2}{1 + \epsilon^4} \right)} }
\mathrm{\delta = \dfrac{1}{1 - \left( \dfrac{5}{6} \cdot \dfrac{ 1,2^2}{1 + 1,2^4} \right)} }
Por fim, o coeficiente de Hahn será:
\mathrm{\delta = 1,64}
Corrigindo então os momentos nas duas direções teremos:
\mathrm{M_x^* = 6,8 \cdot 1,64 = 11,15 \; kN \cdot m / m}
\mathrm{M_y^* = 5,16 \cdot 1,64 = 8,46 \; kN \cdot m / m}
Dimensionamento da área de aço
Nesse momento, já possuímos os valores de momentos fletores a cada metro de largura para cada uma das duas direções.
A partir desses valores, seguiremos conforme o dimensionamento de uma viga t.
O que temos que fazer agora é transformar o momento que está em \mathrm{kN \cdot m / m} para um momento que atue apenas em uma nervura.
Lembrando que as nervuras estão espaçadas a cada 62 cm:
\mathrm{M_x = 11,15 \cdot 0,62 = 6,91 \; kN \cdot m}
\mathrm{M_y = 8,46 \cdot 0,62 = 5,25 \; kN \cdot m}
Agora que já possuímos o momento fletor distribuído em uma nervura, basta que calculemos a armadura como uma viga t.
Para o exemplo, utilizarei nossa calculadora gratuita de flexão simples, inserindo o momento de cálculo em kN.cm, para a dimensão de maior esforço.
\mathrm{M_d = 1,4 \cdot 691 = 968 \; kN \cdot cm}
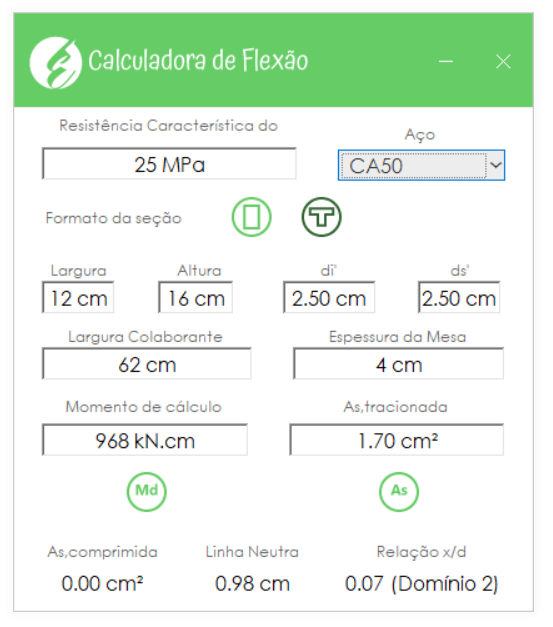
No caso, é necessário uma área de aço de 1,7 cm² em cada nervura. Utilizando a tabela abaixo vamos selecionar armadura necessária.
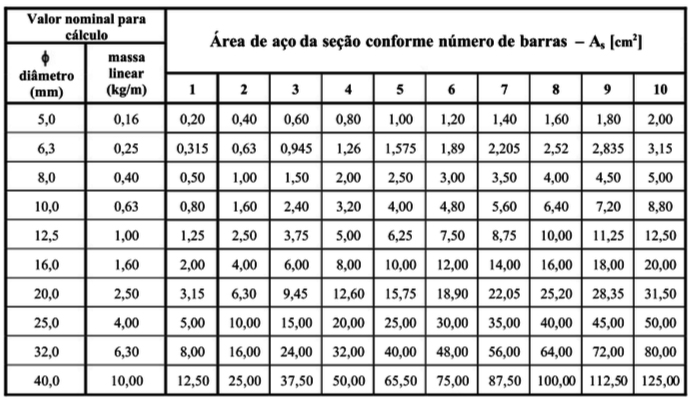
Por fim, podemos utilizar uma barra de 16 mm a cada nervura, o que nos fornece uma área de aço de 2 cm².
Dimensionamento através de softwares
Essa aproximação que utilizamos através das tabelas de Czerny e a correção com o fator apresentado por Hahn geram resultados muitas vezes bem mais elevados do que os reais.
Por isso, é muito importante que o engenheiro domine ferramentas de análise estrutural.
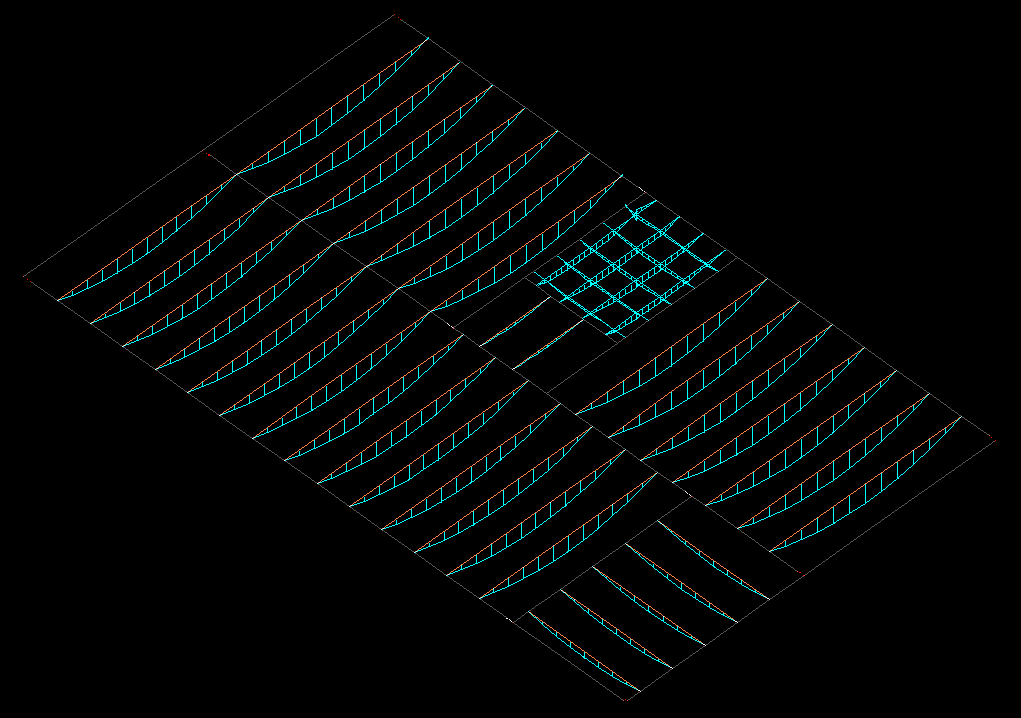
O software TQS possibilita ao engenheiro analisar e dimensionar um conjunto de lajes, inclusive o tipo dimensionado nessa publicação.
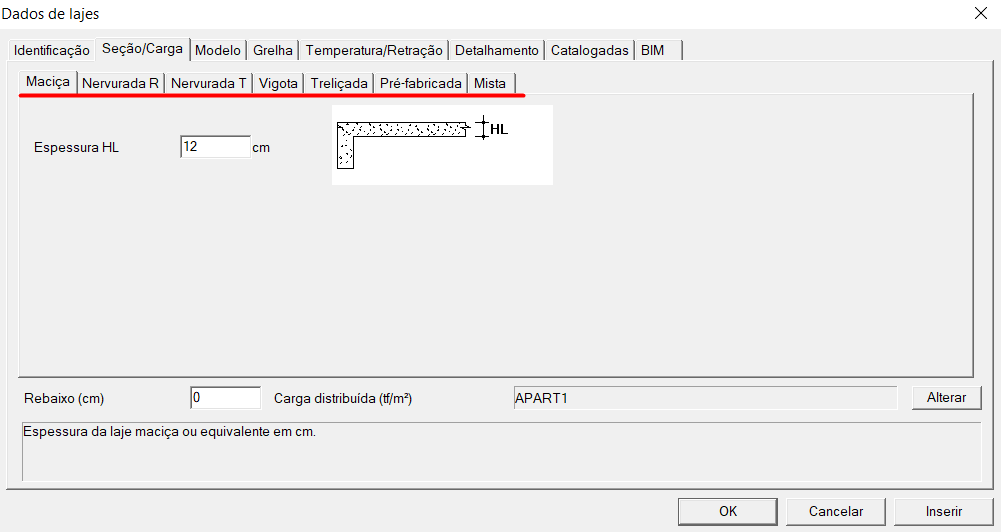
Cabe ao engenheiro configurar completamente os critérios de cálculo para se beneficiar só assim da alta produtividade proporcionada pelo software.
Diante do comentado, convido você a conferir o curso Essencial em Concreto Armado do professor Rangel Lage em que você irá aprender a utilizar o software TQS (na minha opinião, o melhor software do mercado) passando por TODAS as etapas (desde a concepção estrutural até elaboração das pranchas) necessárias para o desenvolvimento de um projeto completo.
Recado final
Esse post tratou apenas da obtenção da armadura de flexão nas nervuras, sendo ainda necessário realizar as verificações de estados limites de serviço, assim como, as demais verificações de estado limite último.
E ai, gostou do post? Deixa um comentário abaixo para que eu possa saber!
Até a próxima!
Fonte:
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014, volume 2. São Carlos: EdUFSCar, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.

muito bom José, fiz um calculo destes utilizando as apostilas do paulo bastos, me gerou algumas duvidas em relação as flechas,
Teria como postar uma verificação das flechas dessa laje.
Obrigado e parabens pelo post.
Fico feliz que tenha gostado, Jefferson!
E obrigado pela sugestão de post.
Abraços!