A análise da estabilidade global de estruturas a princípio pode ser algo um pouco complicado para compreender, mas acredito que com essa leitura você terá um bom início nesse assunto.
Nessa publicação você irá aprender como classificar uma estrutura em nós móveis ou fixos através do parâmetro de instabilidade \mathrm{\alpha}.
Efeitos de segunda ordem
Com o intuito de iniciarmos o estudo sobre a deslocabilidade das estruturas, é importante distinguirmos esforços de primeira e de segunda ordem. Apenas para ilustrar, observe a figura abaixo.
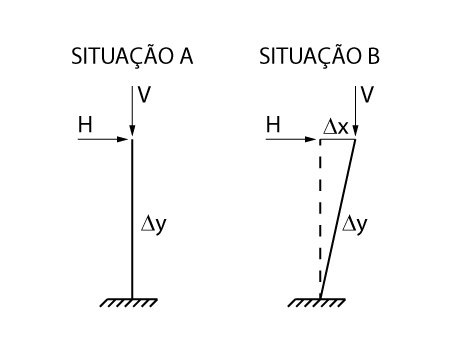
A estrutura em questão, está submetida à uma ação horizontal (esta pode ser uma ação decorrente do vento, empuxo, imperfeição geométrica etc.) e uma ação vertical (peso próprio, sobrecarga de utilização etc.).
Na situação A, em que temos a estrutura ainda indeformada, o momento fletor na base vale \mathrm{M_1 = H \cdot \Delta_y}.
No entanto, observe que a mesma estrutura, após deformada (situação B), apresenta um momento superior ao apresentado acima.
\mathrm{M_2 = H \cdot \Delta_y + V \cdot \Delta_x}
Isso se dá devido ao fato que, após a estrutura deslocada, a ação vertical causa esforços adicionais de flexão no engaste. A esses esforços adicionais, chamamos de esforços de segunda ordem. Enquanto os esforços obtidos com a estrutura indeslocada são chamados de esforços de primeira ordem.
Classificação da estrutura quanto a deslocabilidade
A norma brasileira classifica as estruturas quanto a deslocabilidade em nós fixos e nós móveis. Em primeiro lugar, temos as estruturas de nós fixos, em que os esforços segunda ordem globais, são inferiores a 10% dos esforços de primeira ordem.
No caso da estrutura atender o colocado acima, nós podemos desconsiderar os esforços globais de segunda ordem. Ou seja, durante a nossa análise, caso os esforços de segunda ordem equivalham a 7% (apenas exemplo) dos esforços de primeira ordem, nós podemos desconsiderá-los.
Com o fim de facilitar o entendimento, vamos utilizar o caso apresentado acima. Caso \mathrm{\dfrac{V \cdot \Delta_x}{H \cdot \Delta_y }} seja superior a 0,10, a estrutura é considerada de nós móveis e nós teremos que levar os efeitos globais de segunda ordem em consideração.
Parâmetro de instabilidade alfa
Normalmente o primeiro parâmetro que estudamos a fim de classificar a estrutura em nós móveis ou fixos é o parâmetro de instabilidade \mathrm{\alpha}. O mesmo pode ser obtido a partir da equação abaixo:
\mathrm{\alpha = H_{tot} \cdot \sqrt{\dfrac{N_k}{E_{cs} \cdot I_c}}}
O valor de \mathrm{H_{tot}} indica a altura total da edificação a partir de um ponto pouco deslocável. O \mathrm{N_k} é o somatório de todas as cargas verticais atuantes na estrutura.
Os limites de \mathrm{\alpha} para consideração da estrutura como nós fixos valem:
\mathrm{\alpha_1 = 0,2 + 0,1 \cdot n}, caso n seja igual ou inferior a 3;
\mathrm{\alpha_1 = 0,6}, caso n seja igual ou superior a 4.
Onde \mathrm{n} indica o número pavimentos acima da fundação.
O valor de \mathrm{\alpha_1} varia de acordo com a estrutura de contraventamento, valendo 0,6 para associação de pilares-parede e pórticos, 0,7 para o caso do contravento ser dado apenas por pilares-parede ou 0,5 para o caso em que o contraventamento é dado apenas por pórticos.
Inércia do pilar equivalente para pórticos
A fim de obter a rigidez no caso de pórticos, podemos utilizar a inércia de um pilar equivalente.
Apenas para lembrar da metodologia, devemos aplicar uma força arbitrário no topo do pórtico analisado e então calcularmos o produto de rigidez comparando-o com um pilar engastado na base e e livre no topo.
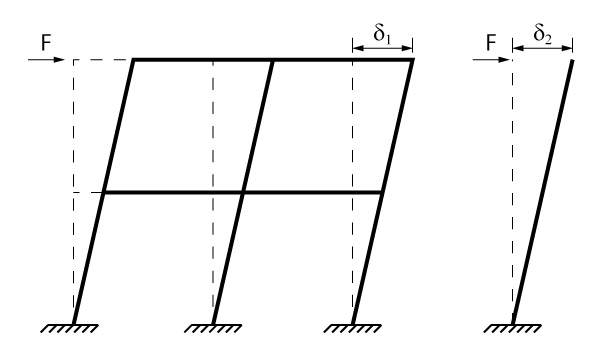
Uma vez que o deslocamento no topo de uma barra engastada na base e livre no topo vale \mathrm{\delta = \dfrac{F \cdot H^3}{3 \cdot \left( E \cdot I \right)}}, podemos calcular o produto de rigidez com base no deslocamento encontrado no topo do pórtico:
\mathrm{\left( E \cdot I \right) = \dfrac{F \cdot H^3}{3 \cdot \delta_2}}
A norma brasileira ainda permite, no caso de uma análise global da estrutura, majorar o módulo de deformação secante em 10%.
Exemplo sobre parâmetro alfa
Com o intuito de colocarmos em prático tudo que foi estudado até o momento, vamos classificar nosso edifício de estudo do vento em nós fixos ou nós móveis. A fim de facilitar o acompanhamento dessa publicação, vou repetir aqui os dados para o edifício.

Caso você prefira, pode acompanhar essa resolução pelo vídeo abaixo:
Esse edifício tem 6 pavimentos, com 3,0 m de pé-direito, totalizando 18,0 m de altura e todas as vigas possuem dimensão de 20 x 50 cm.
Em primeiro lugar, já temos o valor de \mathrm{H_{tot}}, que vale 1800,0 cm.
Em segundo lugar, vamos partir para obtenção do \mathrm{N_k}. Para isso, vou considerar de maneira aproximada, como somatório das cargas verticais, o valor de \mathrm{12 \; kN/cm^2} para lajes de piso e \mathrm{10 \; kN/cm^2} para lajes de forro.
Assim sendo, vamos para o cálculo do somatório das cargas verticais:
\mathrm{N_k = 20 \cdot 30 \cdot \left( 5 \cdot 12 + 1 \cdot 10 \right) = 42.000 \; kN}
Rigidez da estrutura
Por fim, vamos para o cálculo do produto de rigidez da estrutura. Lembre-se que essa verificação deve ser feita para cada direção analisada. Aqui focaremos no vento atuando perpendicular à maior dimensão da edificação.
Módulo de elasticidade secante do concreto
Inicialmente, vamos calcular o módulo de elasticidade secante do concreto. Para isso, consideraremos um concreto de classe C30 (resistência característica de 30 MPa) e granito como agregado graúdo.
Assim sendo, teremos um módulo de elasticidade inicial:
\mathrm{E_{ci} = \alpha_E \cdot 5.600 \cdot \sqrt{f_{ck}}}
\mathrm{E_{ci} = 1,0 \cdot 5.600 \cdot \sqrt{30} = 30.672 \; MPa}
Podemos agora calcular o módulo de elasticidade secante:
\mathrm{E_{cs} = \left( 0,8 + 0,2 \cdot \dfrac{f_{ck}}{80} \right) \cdot E_{ci}}
\mathrm{E_{cs} = \left( 0,8 + 0,2 \cdot \dfrac{30}{80} \right) \cdot 30.672 = 26.838 \; MPa}
Rigidez do pilar equivalente
A estrutura em questão tem dois tipos de pórtico, o de extremidade, que se repete duas vezes, e o intermediário, que se repete 4 vezes, conforme ilustra a figura abaixo:
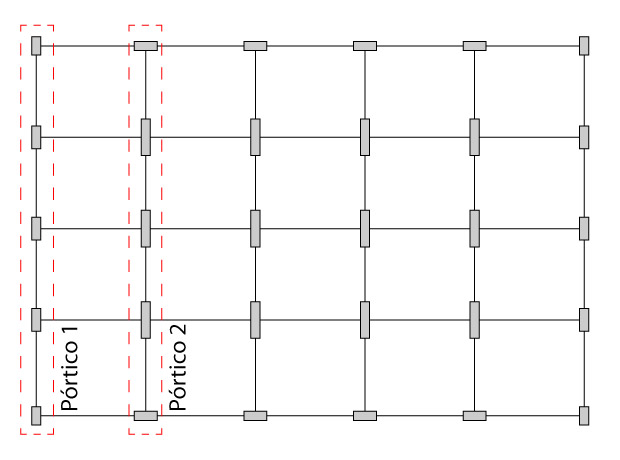
A fim de calcularmos a a rigidez equivalente para os pórticos, vamos obter o deslocamento no topo dos mesmos após a aplicação de uma força arbitrária de 100 kN. Para isso, podemos utilizar algum software comercial, como por exemplo o Ftool.
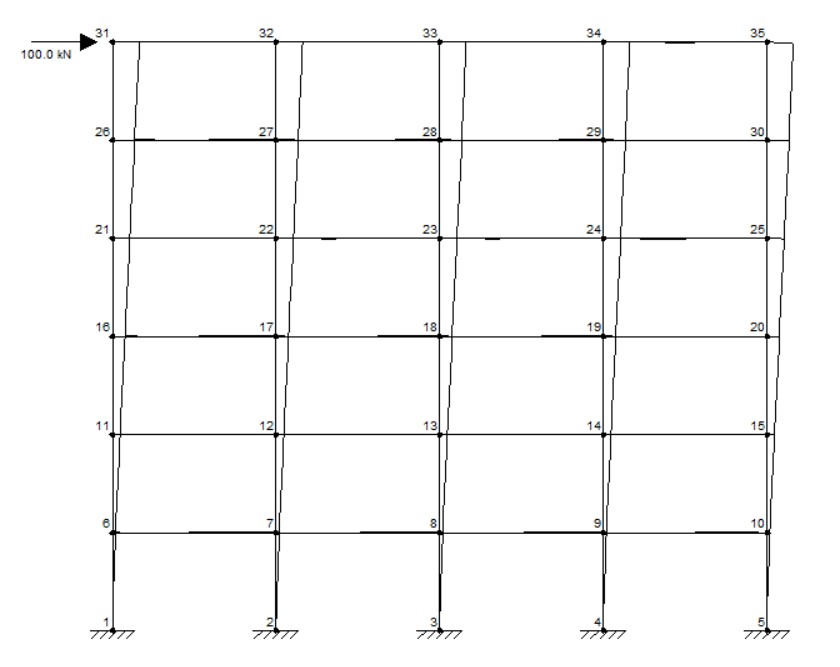
Vamos lembrar que, podemos calcular o deslocamento em um pilar equivalente, engastado e livre, através da equação abaixo:
\mathrm{\delta = \dfrac{F \cdot H^3}{3 \cdot \left( E \cdot I \right)}}
\mathrm{\left( E \cdot I \right) = \dfrac{F \cdot H^3}{3 \cdot \delta}}
Assim sendo, para o pórtico de extremidade teremos:
\mathrm{\left( E \cdot I \right) = \dfrac{100 \cdot 1800^3}{3 \cdot 1,485392} = 1,31 \cdot 10^{11} \; kN \cdot cm^2}
Agora, para o pórtico intermediário:
\mathrm{\left( E \cdot I \right) = \dfrac{100 \cdot 1800^3}{3 \cdot 1,191156} = 1,63 \cdot 10^{11} \; kN \cdot cm^2}
Assim sendo, como teremos 4 repetições para o pórtico intermediário e duas repetições para o pórtico de extremidade, a rigidez total nessa direção vale:
\mathrm{\left( E \cdot I \right) = 2 \cdot 1,31 \cdot 10^{11} + 4 \cdot 1,63 \cdot 10^{11} = 9,15 \cdot 10^{11} \; kN \cdot cm^2}
Resultado do parâmetro de instabilidade \mathrm{\alpha}
Por fim, podemos aplicar a formulação agora:
\mathrm{\alpha = H_{tot} \cdot \sqrt{\dfrac{N_k}{E_{cs} \cdot I_c}}}
\mathrm{\alpha = 1800 \cdot \sqrt{\dfrac{42.000}{9,15 \cdot 10^{11}}} = 0,39}
Visto que temos um edifício de mais de 4 pavimentos e uma estrutura de contraventamento formada apenas por pórticos, teremos \mathrm{\alpha_1 = 0,5}. Dessa forma, uma vez que \mathrm{\alpha < \alpha_1}, podemos classificar a estrutura em questão como de nós fixos.
Recado final
É isso, chegamos ao final de mais um conteúdo. Meus parabéns por estar investindo em sua capacitação!
Espero que nesse momento você saiba como utilizar o parâmetro de instabilidade \mathrm{\alpha} para determinar se os efeitos de segunda ordem são relevantes ou não para sua análise.
Um grande abraço e até o próximo conteúdo.
Otimize seus cálculos de engenharia em minutos. Experimente o Calculadoras de Engenharia.

parabens pela didatica
Obrigado, José!
Parabéns!
Valeu, Ricardo!