Você sabia que a maioria das vigas em edifícios usuais de concreto armado podem ser dimensionadas como viga do formato de T? Pois é, isso se dá devido ao fato de que vigas e lajes não são elementos independentes e, de fato, trabalham em conjunto.
Nas próximas linhas você irá aprender como levar em consideração a interação entre vigas e lajes e como dimensionar uma viga T.
Nomenclaturas e variáveis de uma viga T
Antes de partimos para o equacionamento é importante nomearmos as variáveis e as regiões de uma viga de seção T:
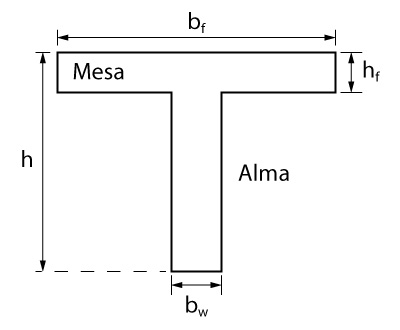
- Mesa: para os casos em que se trata de interação entre viga e laje, equivale a parcela da laje. Também é denominada de flange;
- Alma: para os casos em que se trata de interação entre viga e laje, equivale a própria viga. Também é denominada de nervura;
- \mathrm{b_f}: largura da mesa;
- \mathrm{b_w}: largura da alma;
- \mathrm{h_f}: espessura da mesa;
- \mathrm{h}: altura total da viga.
Largura colaborante de vigas de seção T
Uma vez que vigas e lajes trabalham de maneira monolítica, a tensão normal que surge na viga devido à flexão, não se limita a região da mesma, conforme ilustra a figura abaixo.
A norma brasileira ABNT/NBR: 6118 (2014) nos permite levar em consideração a ação entre viga e laje através da utilização de uma largura colaborante \mathrm{b_f}.
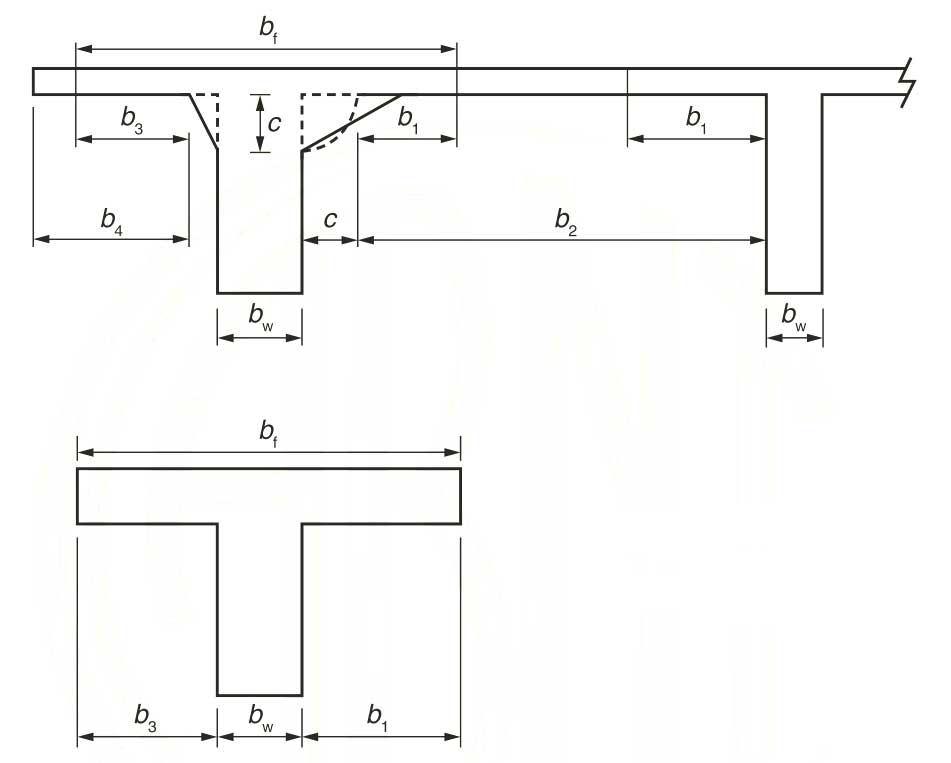
Sabendo que \mathrm{b_2} equivale a distância de face a face entre duas vigas e \mathrm{b_4} equivale a distância da face da viga ao fim da laje (caso não tenha outra viga nesse sentido), os valores \mathrm{b_1} e \mathrm{b_3} que devem ser acrescidos para cada lado, valem:
\mathrm { b_1 \leq \left\{ \begin{array}{ll} 0,5 \cdot b_2 \\ 0,1 \cdot a \end{array} \right. }
\mathrm { b_3 \leq \left\{ \begin{array}{ll} b_4 \\ 0,1 \cdot a \end{array} \right. }
A variável \mathrm{a} equivale a distância entre dois pontos de momento nulo e caso não seja calculada analisando o diagrama de momentos fletores, pode ser estimada em função do comprimento da viga:
a) viga simplesmente apoiada: \mathrm{a=1,00 \cdot l};
b) tramo com momento em uma só extremidade: \mathrm{a=0,75 \cdot l};
c) tramo com momentos nas duas extremidades: \mathrm{a=0,60 \cdot l};
d) tramo em balanço: \mathrm{a=2,00 \cdot l}.
Situações de cálculo de viga T
A diferença entre as formulações utilizadas no dimensionamento de vigas retangulares para uma viga T é que, caso a profundidade da linha neutra seja superior a espessura da mesa, a área comprimida não será mais uma região retangular.
Diante do exposto no parágrafo anterior, o primeiro passo no dimensionamento de um viga de seção T deve ser calcular a altura da linha para analisar se a mesma se encontra dentro da mesa da viga. Esse cálculo é realizado levando em conta uma seção retangular de largura \mathrm{b_f}.
O cálculo da linha pode ser realizado de acordo com a fórmula abaixo:
\mathrm{k=\dfrac{M_{Sd}}{b_f \cdot f_{cd}}}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
A partir desse cálculo teremos duas possibilidades: a linha neutra cair na mesa ou na alma na viga T.
Linha neutra na mesa da viga
Caso a linha neutra caia na mesa da viga, ou seja, \mathrm{x \leq h_f}, a região comprimida será retangular:
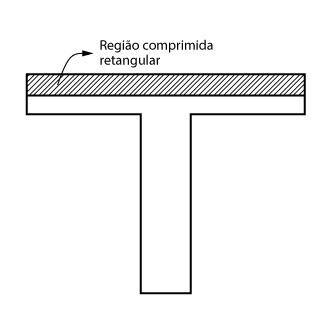
Nessa condição, o cálculo da área de aço será realizado de maneira idêntica a uma viga retangular de largura \mathrm{b_f}.
Linha neutra na alma da viga sem armadura dupla
Caso a linha neutra caia na alma, ou seja, caso \mathrm{x > h_f}, a região comprimida terá um formato de T.
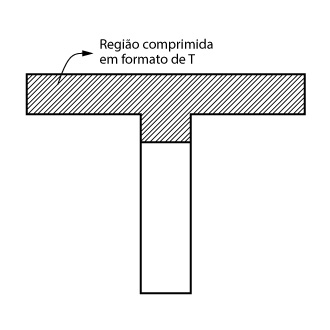
Dessa forma, dividiremos o momento solicitante em duas parcelas: a primeira, \mathrm{M_1}, resistida pelas duas abas da mesa e a segunda parcela, \mathrm{M_2}, resistida pela alma. Para cada uma dessas parcelas serão calculadas as áreas de aço necessárias.
Primeira parcela: compressão nas abas
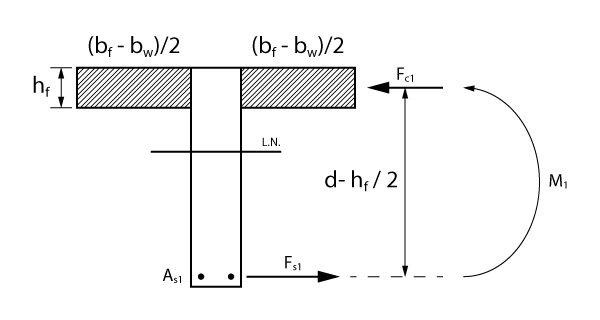
Para a primeira parcela, a área comprimida vale \mathrm{A_{c1} = 2 \cdot \left(\dfrac{b_f - b_w}{2}\right) \cdot h_f}. A força atuante nessa região é calculada apenas multiplicando essa área pela tensão atuante:
\mathrm{F_{c1} = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f}
Agora basta multiplicarmos pelo braço de alavanca (que vale a distância entre o centro de compressão e as barras de aço) para obtermos o momento resistente \mathrm{M_1}:
\mathrm{M_1 = F_{c1} \cdot z_1}
\mathrm{M_1 = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f \cdot \left(d - \dfrac{h_f}{2} \right)}
Segunda parcela: compressão na alma
O momento restante, \mathrm{M_2}, deverá ser resistido pela alma da viga:
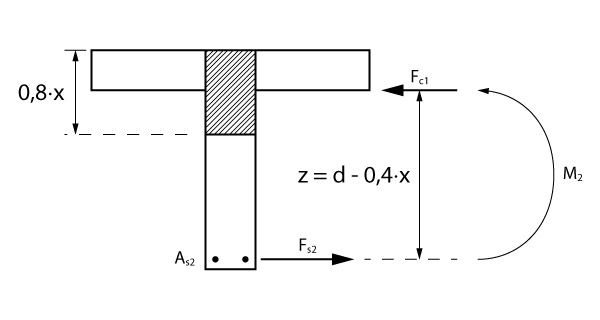
\mathrm{M_2 = M_{Sd} - M_1}
Em posse do momento que deve ser resistido pela alma, o próximo passo é calcular a profundidade da linha neutra real. Essa será calculada pela equação abaixo:
\mathrm{k=\dfrac{M_2}{b_w \cdot f_{cd}}}
\mathrm{x = \dfrac{0,68 \cdot d \pm \sqrt{0,4624 \cdot d^2 - 1,088 \cdot k}}{0,544}}
Repare que já utilizamos essa equação nesse post, as únicas alterações que fizemos foi a utilização de \mathrm{M_2} e \mathrm{b_w}. Basicamente o que estamos calculando é a altura da região de concreto comprimida em uma largura \mathrm{b_w} para resistir a um momento \mathrm{M_2}.
Cálculo da área de aço
Por fim, a área de aço total será o somatório das duas áreas de aço:
\mathrm{A_s = A_{s1} + A_{s2}}
\mathrm{A_s = \dfrac{M_1}{ \left(d - \dfrac{h_f}{2} \right) \cdot f_{yd}} + \dfrac{M_2}{(d - 0,4 \cdot x) \cdot f_{yd}}}
Observe que, essas duas parcelas de áreas de aço foram calculadas considerando as barras escoando. Lembre-se que de acordo com as hipóteses de cálculo a linha neutra é limitada de forma que seja garantido a ductilidade da peça. Dessa forma, o escoamento das barras inferiores é garantido.
Linha neutra na alma com armadura dupla
Caso o cálculo realizado acima resulte em uma linha neutra superior aos valores permitidos por norma (apenas como exemplo, para concretos de até 50 MPa sem distribuição de momentos, o limite vale \mathrm{x = 0,45 \cdot d}), o dimensionamento da viga é realizado com armadura dupla, ou seja, adicionando armação comprimida.
Assim como realizado para armadura dupla em vigas retangulares, o momento também será dividido em parcelas, mas com alguns detalhes a mais. A primeira parcela já foi explicada anteriormente, será o momento resistente apenas pelas abas. A parcela resistida pela alma será dividida em duas, uma parte resistida com a linha neutra fixada no limite de norma e o outra parte equivalente ao restante do momento, em que a compressão será resistida por uma armadura comprimida.
Primeira parcela: compressão nas abas
Então vamos formular o explicado no parágrafo anterior. A primeira parcela, já comentada, vale:
\mathrm{M_1 = 0,85 \cdot f_{cd} \cdot \left( b_f - b_w \right) \cdot h_f \cdot \left(d - \dfrac{h_f}{2} \right)}
Segunda parcela: compressão na alma
A segunda parcela, é apresentada na figura abaixo:
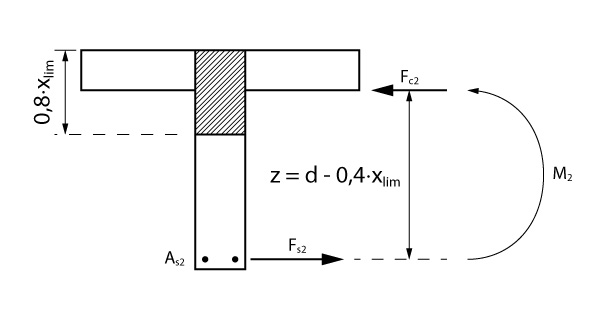
Vamos calcular o momento resistido pela aba igualando o mesmo ao gerado pelo binário apresentado na figura.
\mathrm{M_2 = F_{c2} \cdot (d - 0,4 \cdot x_{lim})}
\mathrm{M_2 = F_{c2} \cdot (d - 0,4 \cdot (0,45 \cdot d))}
\mathrm{M_2 = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot x_{lim} \cdot 0,82 \cdot d}
\mathrm{M_2 = 0,85 \cdot f_{cd} \cdot b_w \cdot 0,8 \cdot 0,45 \cdot d \cdot 0,82 \cdot d}
\mathrm{M_2 = 0,251 \cdot f_{cd} \cdot b_w \cdot d^2}
Agora que o momento foi calculado, podemos obter a área de aço necessária para essa parcela:
\mathrm{M_2 = F_{s2} \cdot (d - 0,4 \cdot x_{lim})}
\mathrm{M_2 = F_{s2} \cdot (d - 0,4 \cdot (0,45 \cdot d))}
\mathrm{M_2 = F_{s2} \cdot 0,82 \cdot d}
\mathrm{M_2 = A_{s2} \cdot f_{yd} \cdot 0,82 \cdot d}
\mathrm{A_{s2} = \dfrac{M_2}{0,82 \cdot d \cdot f_{yd}}}
Terceira parcela: restante do momento com compressão na armadura comprimida
A última parcela, ilustrada na figura abaixo, é resistida pelo binário gerado pela armadura tracionada, \mathrm{A_{s3}}, e a armadura comprimida \mathrm{A_s '}.
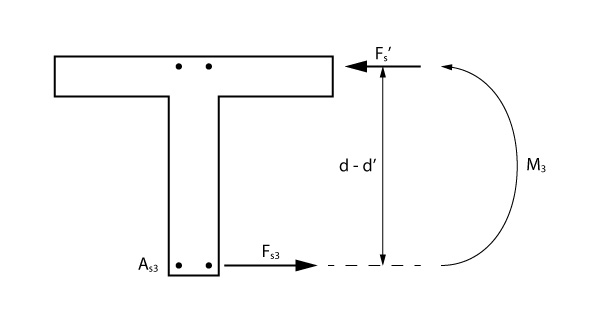
O valor da parcela \mathrm{M_3} representa o restante do momento solicitante de cálculo:
\mathrm{M_3 = M_{Sd} - M_1 - M_2}
Armadura tracionada
Podemos então, calcular a armadura de tração para resistir a esse momento:
\mathrm{M_3 = F_{s3} \cdot (d - d')}
\mathrm{M_3 = A_{s3} \cdot f_{yd} \cdot (d - d')}
\mathrm{A_{s3} = \dfrac{M_3 }{(d - d') \cdot f_{yd}}}
Repare que novamente calculamos a armadura inferior com a tensão igual a tensão de escoamento. Isso é garantido por termos a certeza, uma vez que limitamos profundidade da linha neutra, que a seção se encontra no domínio 3.
Armadura comprimida
Conforme comentando para armadura dupla de vigas retangulares, não temos a garantia que a armadura comprimida esteja escoando. Sabendo que o para o domínio 3 o encurtamento no concreto vale 3,5 ‰, é possível calcular a deformação na armadura comprimida:
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (x_{lim} - d')}{x_{lim}}}
\mathrm{\epsilon_s ' = \dfrac{0,0035 \cdot (0,45 \cdot d - d')}{0,45 \cdot d}}
Com a deformação calculada o próximo passo é obter a tensão atuante da armadura:
\mathrm { f_s ' = \left\{ \begin{array}{ll} 21.000 kN/cm^2 \cdot \epsilon_s '; se \epsilon_s ' < \epsilon_{yd} \\ f_{yd}; se \epsilon_s ' \geq \epsilon_{yd} \end{array} \right. }
Por fim, a armação adicionada na região comprimida vale:
\mathrm{A_s ' = \dfrac{M_3}{(d - d') \cdot f_s '}}
Resumo da área de aço
Para a região tracionada da viga será adicionada a área de aço equivalente ao somatório das três áreas abaixo:
\mathrm{A_s = A_{s1} + A_{s2} + A_{s3}}
E para a região comprimida da viga será adicionada a área de aço \mathrm{A_s '}.
Parabéns por ter chegado até aqui! Agora que você já está afiado na teoria, o próximo passo é avançar para a resolução de exercícios a fim de fixar os conteúdos aprendidos. Dúvidas e sugestões são sempre bem vindos nos comentários abaixo.
Até a próxima!
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 1
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
CARVALHO, R. C.; FIGUEIREDO FILHO, J. R. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado Segundo a NBR 6118:2014. São Carlos: EdUFSCar, 2014.
Otimize seus cálculos de engenharia em minutos. Experimente o Calculadoras de Engenharia.

Gostei muito do desenvolvimento teórico, mas penso que deveria vir acompanhado de exemplos práticos para facilitar o entendimento de alunos de graduação.
Muito obrigado pelo comentário, Sebastião!
No post eu coloquei um link para um post de exercícios:
https://www.guiadaengenharia.com/dimensionamento-viga-t-exemplos/
Grande abraço!
Olá, gostaria de usar a imagem dessas vigas no meu perfil profissional de engenharia no Instagram!
Seria possível?
Olá, Nicolly,
Espero que esteja tudo tranquilo contigo
Basta marcar nosso Instagram como fonte
Abraço