Nesse segunda parte da série de posts de dimensionando um reservatório elevado iremos entrar na parte dos dimensionamentos das áreas de aço a partir os esforços calculados anteriormente.
Dessa forma, nessa publicação irei abordar, respectivamente, como dimensionar a área de aço para uma reservatório como placa e como viga e as verificações de tensões e ancoragens no apoio.
Dimensionamento do reservatório como placa
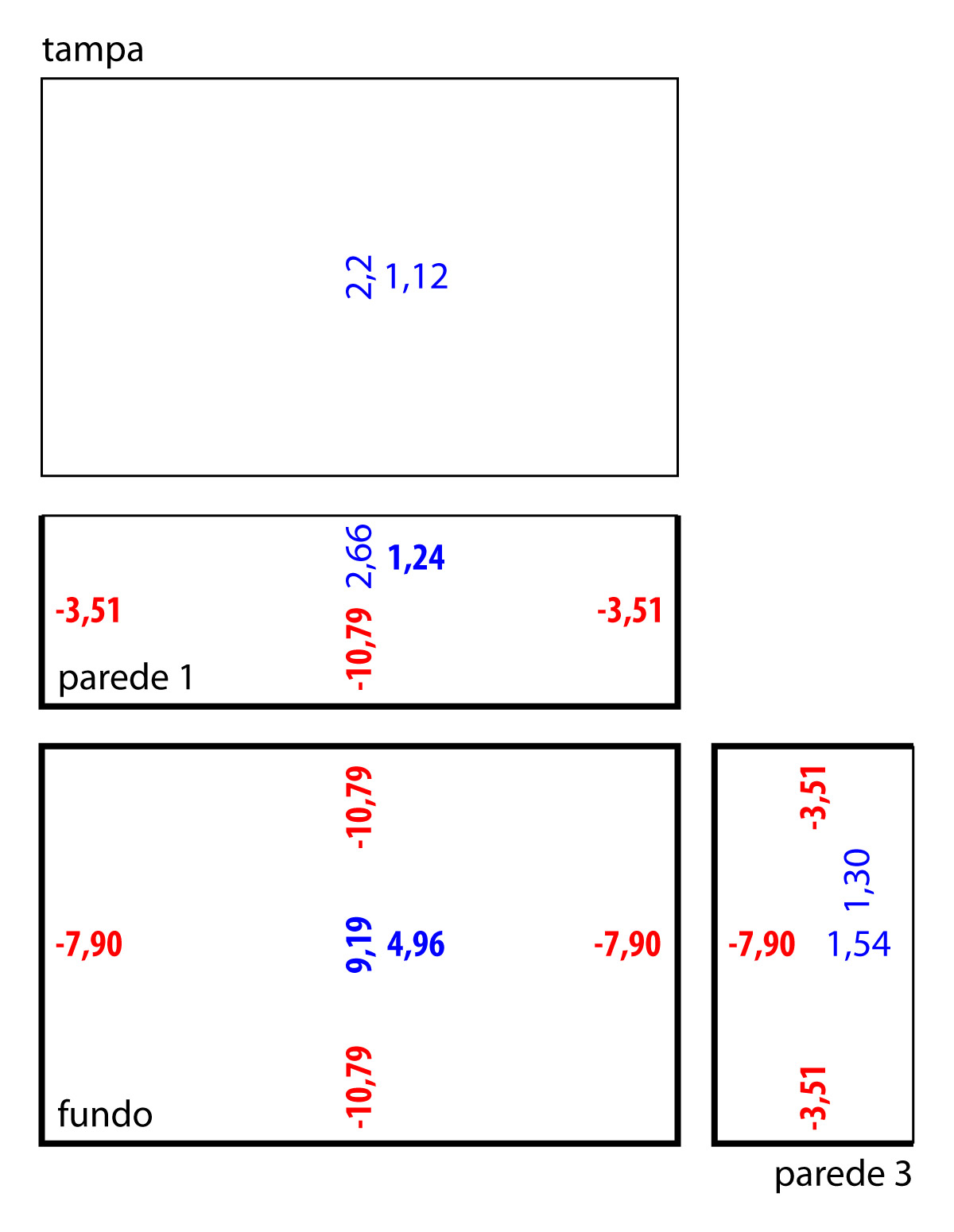
Apenas para facilitar a leitura desse post, irei repetir os esforços, já compatibilizados, encontrados na etapa anterior desse mesmo dimensionamento:
Considerações gerais
Iremos considerar a Classe de Agressividade Ambiental (CAA) como II, o cobrimento nominal de 2,5 cm, a resistência característica do concreto (fck) como 25 MPa e o aço como CA50 (tensões de escoamento de cálculo de 500 MPa).
Em todas as situações do dimensionamento como lajes, utilizaremos uma seção de 100 cm de largura, a fim de obter áreas de aço a cada metro. Lembre-se que os esforços obtidos anteriormente são para cada metro de largura.
Laje de fundo do reservatório
Na laje de fundo temos os momentos característicos positivos de \mathrm{9,19 \; kN \cdot m / m} e \mathrm{4,96 \; kN \cdot m / m}. Consideraremos a altura útil como 12 cm, ou seja, uma vez que o cobrimento é de 2,5 cm, estou estimando uma bitola longitudinal de 10 mm.
Para o dimensionamento poderíamos seguir basicamente conforme o dimensionamento de seções de concreto à flexão, mas para facilitar utilizaremos nossa calculadora de flexão simples, disponibilizada gratuitamente aqui no blog.
Como temos os momentos característico, é necessário obter também os momentos de cálculo:
\mathrm{M_d = \gamma_f \cdot M_k = 1,4 \cdot 919 = 1287 \; kN \cdot cm}
\mathrm{M_d = 1,4 \cdot 496 = 1287 \; kN \cdot cm}

Para a outro direção a calculadora retornou o valor de \mathrm{1,35 \; cm^2 / m}.
É importante lembrar do que vimos em no detalhamento de lajes maciças, e calcularmos também a área de aço mínima para a seção. No caso irá valer:
\mathrm{A_{s,mín} = 0,67 \cdot \dfrac{0,15}{100} \cdot b \cdot h }
\mathrm{A_{s,mín} = 0,67 \cdot \dfrac{0,15}{100} \cdot 100 \cdot 15 = 1,51 \; cm^2 / m }
Sendo assim, teremos as áreas de aço de \mathrm{2,54 \; cm^2/m} em uma direção e \mathrm{1,51 \; cm^2/m} na outra.
[formulario-calculadora-flexao]Com essa área de aço por metro podemos obter uma bitola e um espaçamento com a utilização da tabela abaixo:

A fim de simplificar o detalhamento do reservatório utilizarei barras de 8 mm a cada 20 cm para a direção de maior momento e barras de 6,3 mm espaçadas a cada 20 cm para a direção de menor momento.
Laje de tampa do reservatório
Na laje de tampa, seguindo o mesmo valor de cobrimento e de bitola estimada, utilizaremos uma altura útil de 7 cm.
A armadura mínima também será diferente, uma vez que a espessura da laje é menor:
\mathrm{A_{s,mín} = 0,67 \cdot \dfrac{0,15}{100} \cdot b \cdot h }
\mathrm{A_{s,mín} = 0,67 \cdot \dfrac{0,15}{100} \cdot 100 \cdot 10 = 1,00 \; cm^2 / m }
Inserindo o maior esforço, que vale \mathrm{2,2 \; kN \cdot m / m}, na calculadora:
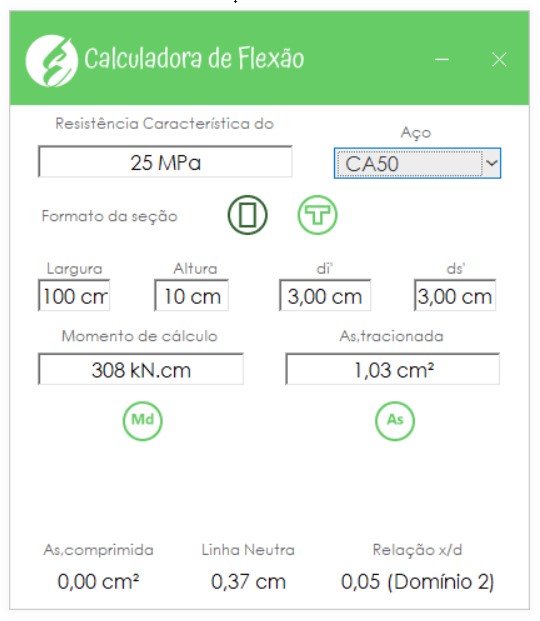
Vale lembrar que o valor que inserimos na calculadora é o momento de cálculo e não o característico.
Utilizaremos o valor encontrado, que é muito próximo da armadura mínima (3% de diferença), para as duas direções.
Entrando novamente na tabela já apresentada acima chegamos em barras de 5 mm espaçadas a cada 20 cm nas duas direções.
Paredes 1, 2, 3 e 4
No caso das paredes, como temos a mesma espessura da laje de fundo, seguiremos com os mesmos valores para altura útil e para armadura mínima.
O maior momento positivos entre todas as paredes vale \mathrm{2,66 \; kN \cdot m / m}, que ao inserir na calculadora encontraremos o área de aço de \mathrm{0,72 \; cm^2/m}. Essa área de aço é inferior a área de aço mínima de \mathrm{1,51 \; cm^2/m}.
Assim sendo, utilizaremos barras de 6,3 mm com espaçamento de 20 cm.
Ligação entre fundo e as paredes 1 e 2
Entre o fundo e as paredes 1 e 2 temos um momento negativo de \mathrm{10,79 \; kN \cdot m / m}. Para o momento fletor negativo a armadura mínima vale:
\mathrm{A_{s,mín} = \dfrac{0,15}{100} \cdot b \cdot h }
\mathrm{A_{s,mín} = \dfrac{0,15}{100} \cdot 100 \cdot 15 = 2,25 \; cm^2 / m }
Entrando com o momento de cálculo no software encontramos a armadura de \mathrm{3,00 \; cm^2/m}:
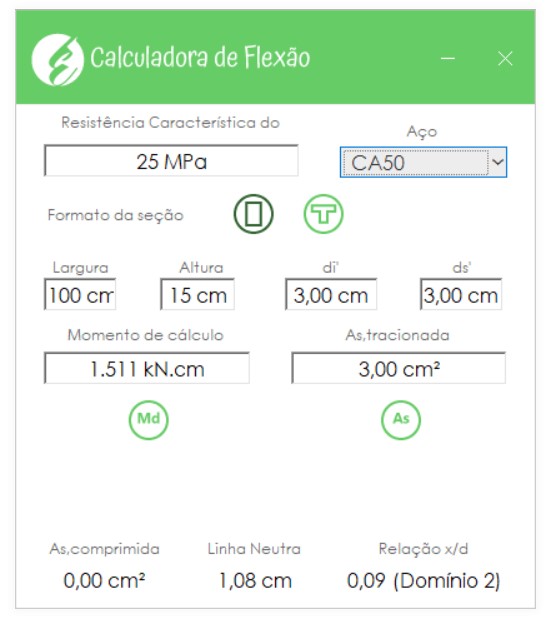
O que resulta em um detalhamento com barras de 8 mm espaçadas a cada 15 cm.
Ligação do fundo com as paredes 3 e 4
No caso das paredes 3 e 4, atua um momento de \mathrm{7,9 \; kN \cdot m / m} na ligação com o fundo. Esse momento gera uma armação de \mathrm{2,18 \; cm^2/m}, que é inferior a armadura mínima de \mathrm{2,25 \; cm^2/m}.
Assim sendo, utilizaremos barras de 8 mm espaçadas a cada 20 cm.
Conclusão
Com isso, já dimensionamos os elementos como placa. Vamos partir agora para o dimensionamento dos mesmos como viga.
Dimensionamento do reservatório como viga
Vamos analisar agora as paredes para os carregamentos atuando no próprio plano médio. Irá atuar o peso próprio das paredes, o revestimento das mesmas e o carregamento oriundo da laje de fundo e da laje de tampa.
Paredes 1 e 2
A parede 1 recebe uma carga de \mathrm{3,52 \; kN/m} da tampa, \mathrm{22,94 \; kN/m} da laje de fundo.
O peso próprio distribuído por metro pode ser calculado por:
\mathrm{g_1 = 25 \cdot 0, 15 \cdot 2,19 = 8,21 \; kN/m}
Considerando o revestimento como \mathrm{1,00 \; kN/m^2}, temos:
\mathrm{g_2 = 1,0 \cdot 2,19 = 2,19 \; kN/m}
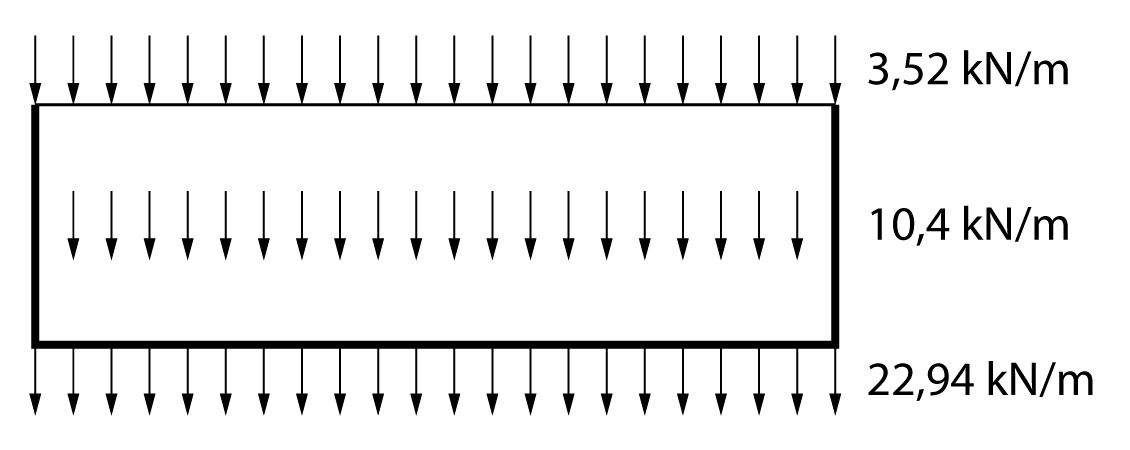
Assim sendo, a carga total atuando na parede 1 vale \mathrm{36,86 \; kN/m}
Antes de partirmos para o dimensionamento em si, é necessário verificarmos antes se a mesma se trata de uma viga esbelta ou uma viga-parede:
\mathrm{\dfrac{l}{h} = \dfrac{4,09}{2,19} = 1,87 < 2,00}
Dessa forma, como se trata de uma viga biapoiada, podemos considera-la como uma viga-parede.
Obtenção dos esforços
Vamos começar com o cálculo do momento fletor na viga-parede:
\mathrm{M_k = \dfrac{q \cdot l^2}{8}}
\mathrm{M_k = \dfrac{36,86 \cdot 4,09^2}{8} = 77,1 \; kN \cdot m}
Agora vamos obter as reações de apoio da mesma:
\mathrm{R_k = \dfrac{q \cdot l}{2}}
\mathrm{R_k = \dfrac{36,86 \cdot 4,09}{2} = 75 \; kN}
Dimensionamento da parede
Como se trata de uma viga-parede não será possível utilizar a calculadora de flexão nesses dimensionamentos.
O primeiro passo para o dimensionamento dessa viga-parede é a obtenção do braço de alavanca:
\mathrm{Z = 0,15 \cdot h \cdot \left( 3 + \dfrac{l}{h} \right)}
\mathrm{Z = 0,15 \cdot 2,19 \cdot \left( 3 + \dfrac{4,09}{2,19} \right) = 1,6 \; m}
Agora podemos dimensionar a área de aço:
\mathrm{A_s = \dfrac{M_d}{Z \cdot f_{yd}}}
\mathrm{A_s = \dfrac{1,4 \cdot 77,1}{1,6 \cdot 43,48} = 1,55 \; cm^2}
Para a armadura mínima em vigas-parede utilizaremos aqui a tabela apresentada em Araújo (2014). A mesma relaciona a área de aço mínima de vigas-parede com a área de aço mínima de vigas esbeltas.
\mathrm{A_{s,minVP} = \lambda \cdot A_{s,minVE}}
Onde o \mathrm{\lambda} pode obtido na tabela abaixo:
| \mathrm{\dfrac{l}{h}} | \mathrm{\lambda} |
|---|---|
| 2,0 | 1,00 |
| 1,5 | 0,90 |
| 1,25 | 0,75 |
| 1,0 | 0,55 |
Apesar da possibilidade de interpolarmos os valores da tabela, aqui utilizarei o valor de 2,0 na relação entre vão e altura, que é o dado de entrada. Assim, a armadura mínima será a mesma que utilizamos em vigas esbeltas:
\mathrm{A_{s,mín} = \dfrac{0,15}{100} \cdot b \cdot h }
\mathrm{A_{s,mín} = \dfrac{0,15}{100} \cdot 15 \cdot 219 = 4,93 \; cm^2}
Vamos utilizar uma tabela de quantidade x bitola para chegarmos em uma área de aço:
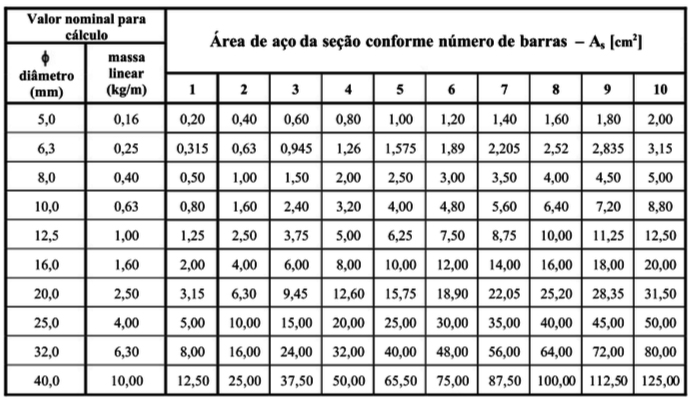
Observando a tabela vemos que é possível cobrir a área de aço mínima com 4 barras de 12,5 mm. Utilizaremos então essa solução, distribuída em duas camadas.
Verificação das tensões no apoio
Vamos calcular primeiro a altura do nó de apoio. O mesmo vale duas vezes o valor de d’.
\mathrm{tg \theta = \dfrac{4 \cdot Z}{l} = \dfrac{4 \cdot 1,6}{4,09}}
\mathrm{tg \theta = 1,5648 \rightarrow \theta = 57 º}
Sabendo que a altura do nó do apoio vale duas vezes \mathrm{d'} e considerando d’ como 5,25 cm (lembre-se que temos barras de aço distribuídas em duas camadas), temos:
\mathrm{u = 2 \cdot d' = 10,5 > c \cdot cotg \theta}
\mathrm{10,5 > 15 \cdot cotg 57 º = 9,74}
Assim sendo devemos verificar se \mathrm{\sigma_d < f_{cdr}}:
\mathrm{\sigma_d = \dfrac{R_d}{b \cdot c}}
\mathrm{\sigma_d = \dfrac{1,4 \cdot 75}{15 \cdot 15} = 0,47 \; kN/cm^2}
Verificando agora a tensão resistente:
\mathrm{f_{cdr} = 0,6 \cdot \left( 1 - \dfrac{f_{ck}}{250} \right) \cdot f_{cd}}
\mathrm{f_{cdr} = 0,6 \cdot \left( 1 - \dfrac{25}{250} \right) \cdot \dfrac{2,5}{1,4} = 0,96 \; kN/cm^2 }
Cálculo da ancoragem
O valor calculado para o meio do vão foi \mathrm{A_s = 1,55 \; cm^2} e o apoio tem que ancorar 80% desse valor:
\mathrm{A_s = 0,8 \cdot 1,55 = 1,24 \; cm^2}
Para um fck de 25 MPa, região de boa aderência e barras de 12,5 mm, temos um comprimento básico de ancoragem de 47 cm. Vale ressaltar que nosso foco aqui não é o estudo da ancoragem, de modo que o detalhamento desse conteúdo entrará em outra publicação.
Assim sendo, com a utilização de ganchos temos o seguinte comprimento necessário:
\mathrm{l_{b,nec} = 0,7 \cdot l_b \cdot \dfrac{A_{s,cal}}{A_{se}}}
\mathrm{l_{b,nec} = 0,7 \cdot 47 \cdot \dfrac{1,24}{5,00} = 8,16 \; cm}
Considerando o mínimo de 10 cm de ancoragem, há espaço disponível para a mesma.
Paredes 3 e 4
Na parede 3 iremos mais direto ao ponto, uma vez que segue os conceitos utilizados nas paredes anteriores.
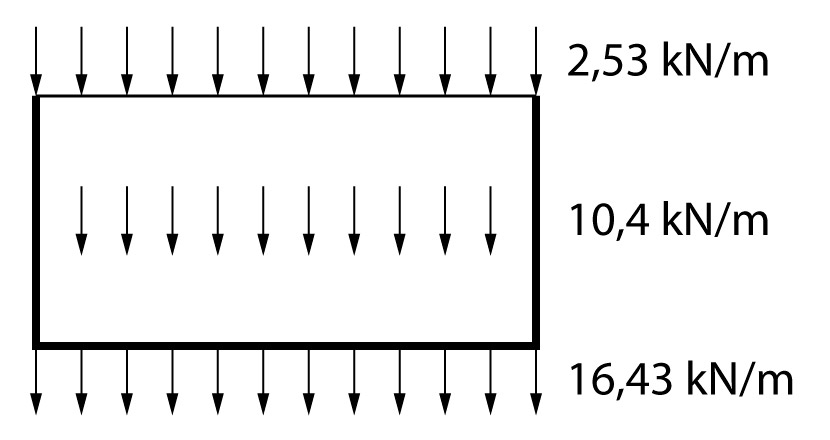
A carga total na parede 3 vale \mathrm{2,53 + 16,43 + 8,21 + 2,19 = 29,36 \; kN/m}
Como a relação entre as dimensões da parede é mais próxima do que a anterior, fica mais evidente que se trata de uma viga-parede:
\mathrm{\dfrac{l}{h} = \dfrac{2,59}{2,19} = 1,18 < 2,00}
Assim sendo, podemos considera-la como uma viga-parede.
Obtenção dos esforços
Vamos começar com o cálculo do momento fletor na viga-parede:
\mathrm{M_k = \dfrac{q \cdot l^2}{8}}
\mathrm{M_k = \dfrac{29,36 \cdot 2,59^2}{8} = 24,62 \; kN \cdot m}
Agora vamos obter as reações de apoio da mesma:
\mathrm{R_k = \dfrac{q \cdot l}{2}}
\mathrm{R_k = \dfrac{29,36 \cdot 2,59}{2} = 38 \; kN}
Dimensionamento da parede
Como se trata de uma viga-parede não será possível utilizar a calculadora de flexão nesses dimensionamentos.
O primeiro passo para o dimensionamento dessa viga-parede é a obtenção do braço de alavanca:
\mathrm{Z = 0,15 \cdot h \cdot \left( 3 + \dfrac{l}{h} \right)}
\mathrm{Z = 0,15 \cdot 2,19 \cdot \left( 3 + \dfrac{2,59}{2,19} \right) = 1,37 \; m}
Agora podemos dimensionar a área de aço:
\mathrm{A_s = \dfrac{M_d}{Z \cdot f_{yd}}}
\mathrm{A_s = \dfrac{1,4 \cdot 24,62}{1,37 \cdot 43,48} = 0,58 \; cm^2}
Utilizando novamente a tabela apresentada em Araújo (2014):
| \mathrm{\dfrac{l}{h}} | \mathrm{\lambda} |
|---|---|
| 2,0 | 1,00 |
| 1,5 | 0,90 |
| 1,25 | 0,75 |
| 1,0 | 0,55 |
Para essa parede, consideraremos a relação entre as dimensões como 1,25. Dessa forma, a armadura mínima para viga-parede será 75% da encontrada para viga esbelta.
\mathrm{A_{s,mín} = 0,75 \cdot \dfrac{0,15}{100} \cdot b \cdot h }
\mathrm{A_{s,mín} = 0,75 \cdot \dfrac{0,15}{100} \cdot 15 \cdot 219 = 3,7 \; cm^2}
Ao utilizar a mesma tabela de área por quantidade apresentada anteriormente, mesmo com uma armadura mínima inferior, continuaremos utilizando 4 barras de 12,5 mm em duas camadas.
Verificação das tensões no apoio
Vamos calcular primeiro a altura do nó de apoio. O mesmo vale duas vezes o valor de d’.
\mathrm{tg \theta = \dfrac{4 \cdot Z}{l} = \dfrac{4 \cdot 1,6}{2,59}}
\mathrm{tg \theta = 2,47 \rightarrow \theta = 68 º}
Sabendo que a altura do nó do apoio vale duas vezes \mathrm{d'} e considerando d’ como 5,25 cm (lembre-se que temos barras de aço distribuídas em duas camadas), temos:
\mathrm{u = 2 \cdot d' = 10,5 > c \cdot cotg \theta}
\mathrm{10,5 > 15 \cdot cotg 68 º = 6,1}
Assim sendo devemos verificar se \mathrm{\sigma_d < f_{cdr}}:
\mathrm{\sigma_d = \dfrac{R_d}{b \cdot c}}
\mathrm{\sigma_d = \dfrac{1,4 \cdot 38}{15 \cdot 15} = 0,24 \; kN/cm^2}
Verificando agora a tensão resistente:
\mathrm{f_{cdr} = 0,6 \cdot \left( 1 - \dfrac{f_{ck}}{250} \right) \cdot f_{cd}}
\mathrm{f_{cdr} = 0,6 \cdot \left( 1 - \dfrac{25}{250} \right) \cdot \dfrac{2,5}{1,4} = 0,96 \; kN/cm^2 }
Cálculo da ancoragem
O valor calculado para o meio do vão foi \mathrm{A_s = 0,58 \; cm^2} e o apoio tem que ancorar 80% desse valor:
\mathrm{A_s = 0,8 \cdot 0,58 = 0,46 \; cm^2}
Para um fck de 25 MPa, região de boa aderência e barras de 12,5 mm, temos um comprimento básico de ancoragem de 47 cm. Vale ressaltar que nosso foco aqui não é o estudo da ancoragem, de modo que o detalhamento desse conteúdo entrará em outra publicação.
Assim sendo, com a utilização de ganchos temos o seguinte comprimento necessário:
\mathrm{l_{b,nec} = 0,7 \cdot l_b \cdot \dfrac{A_{s,cal}}{A_{se}}}
\mathrm{l_{b,nec} = 0,7 \cdot 47 \cdot \dfrac{0,46}{5,00} = 3,16 \; cm}
Considerando o mínimo de 10 cm de ancoragem, há espaço disponível para a mesma.
Recado final
Nesse momento já obtemos todos os esforços, dimensionamos todas as áreas de aço necessárias do reservatório tanto como placa quanto como vigas-parede.
Para darmos esse reservatório por concluído falta apenas verificarmos a fissuração do mesmo e partirmos para o detalhamento em si, mas isso é um assunto para a nossa próxima publicação.
Caso esse conteúdo tenha sido útil para você, compartilhe com um amigo que você acredita que também tem interesse.
Fonte:
ARAÚJO, J. M. Curso de Concreto Armado. Rio Grande: Editora Dunas, 2014. v. 4
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro, 2014.
Gostaria de ter acesso a um curso sobre modelagem de alvenaria estrutural no Revit?
Aproveite enquanto está com um preço especial.
